/es/fraccionarios/fracciones-negativas-y-con-signos/content/

Fracciones equivalentes

El concepto de fracción equivalente es indispensable para sumar o restar fracciones.  Si quieres seguir comprendiendo el mundo de las fracciones debes conocerlo.

Analicemos la siguiente situación: Adda y Diego están en una pista de atletismo de metros de largo.  Adda le dice a Diego que corre más que él porque puede hacerlo sin parar dos sextos de la pista.  Sin embargo él responde que no es cierto puesto que él puede correr un tercio de la pista sin parar.  ¿Quién tiene la razón?

Para responder esta pregunta debemos calcular con precisión cuántos metros recorre cada uno, empecemos por Adda:

Como ella recorre de la pista, debemos dividir el largo de la misma en seis: así sabemos que cada una de las seis partes mide metros.  El dos en el símbolo indica que recorre dos de esas seis partes: por lo tanto Adda recorre metros sin parar.

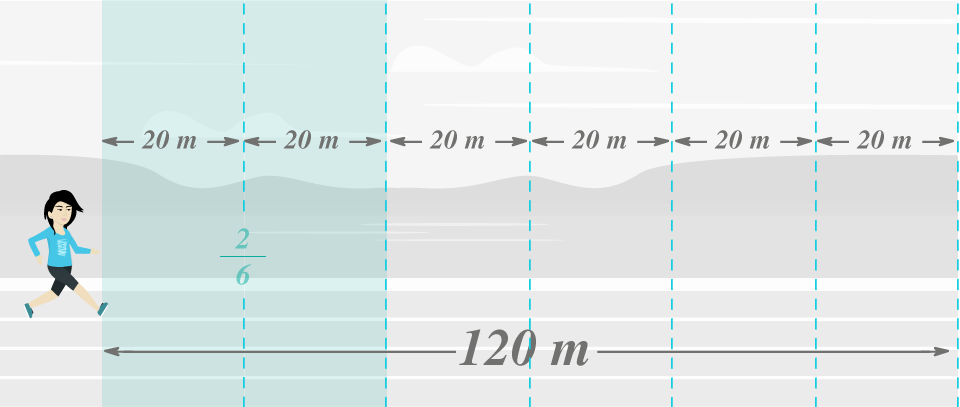
Diego recorre un tercio, debemos dividir el largo de la pista en tres partes.  Realizamos la división .  El uno del símbolo indica que avanza solo una de esas partes, así sabemos que recorre metros:

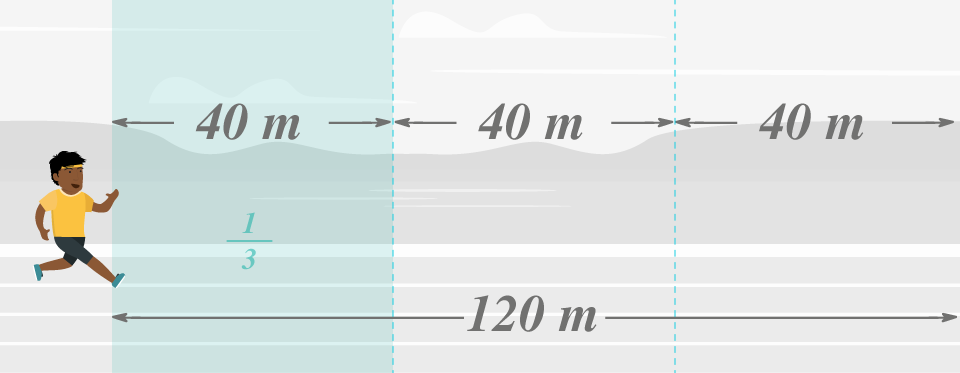
Aunque las distancias recorridas por Adda y Diego se representan por fracciones diferentes resultaron ser iguales, en ese caso se dice que las fracciones y son equivalentes, pues representan la misma cantidad.  Escribimos entonces .  A través del siguiente interactivo puedes observar una interpretación gráfica de lo anterior:

¿Cómo saber si dos fracciones son equivalentes?

Es importante saber cuando dos fracciones son equivalentes, existe una manera sencilla de hacerlo.  Veamos: 

Dadas las fracciones y , si los productos  y  son iguales, las fracciones son equivalentes. 

Es decir, se debe multiplicar “en cruz”, como lo muestra la siguiente imagen:

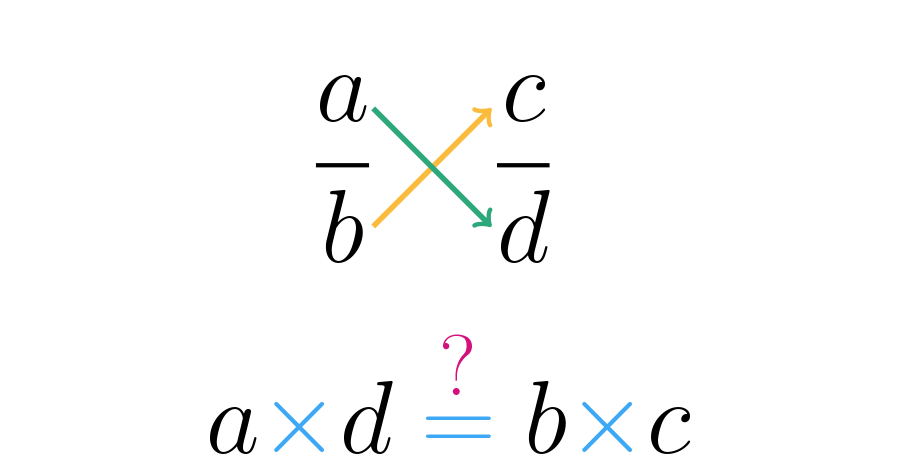
Recuerda que estos productos son los mismo que se hacen para determinar cuando una fracción es mayor que otra.

Observa un ejemplo: ¿son las fracciones y equivalentes?  Como , podemos asegurar que lo son.

Otro ejemplo

¿son las fracciones y equivalentes?  Es decir, ¿representan las misma cantidad?

Para comprobarlo, realizamos los productos cruzados:

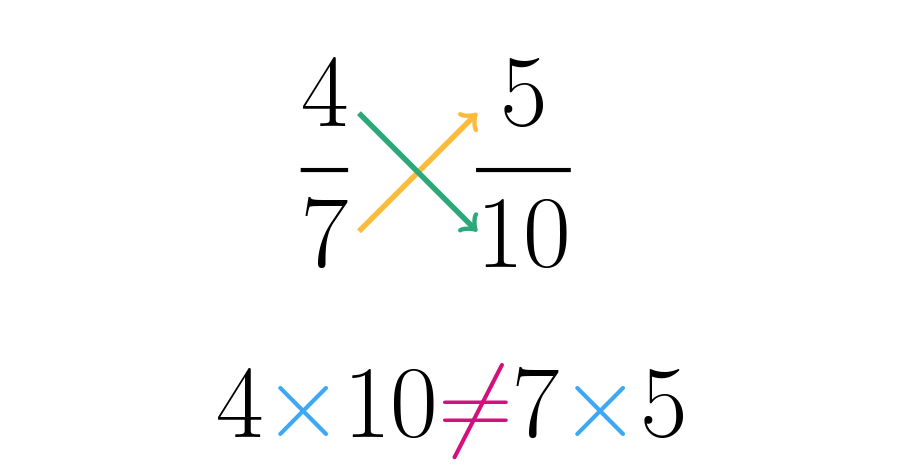
Como los resultados de las multiplicaciones no son iguales, decimos que no son equivalentes.

En este caso escribimos pues este par de símbolos no representan la misma cantidad.

/es/fraccionarios/fracciones-equivalentes-a-enteros-y-naturales/content/