Fraccionarios
Fracciones como partes de una totalidad


/es/fraccionarios/fracciones-como-partes-de-la-unidad/content/
Además de poderse interpretar como partes de unidad, las fracciones se pueden entender como partes de una totalidad compuesta por muchas unidades.
Observa el siguiente ejemplo: dos niños reunieron dinero para comprar una caja de postres de doce unidades, como pusieron sumas de dinero diferentes les corresponden partes diferentes, al primero le corresponden de la caja y al segundo . ¿Cuántos postres le corresponden a cada niño?
En este caso nuestra unidad no es un solo objeto como una pizza, ahora está compuesta por muchas unidades. Para calcular cuánto le corresponde al primer niño dividimos la unidad en el número de partes iguales que señale el denominador y tomamos tantas de esas partes como lo denote el numerador.
Como lo indica el tres en el denominador de , debemos dividir nuestra unidad en tres. Posteriormente, como lo dice el dos en el numerador, tomamos dos de esas partes.
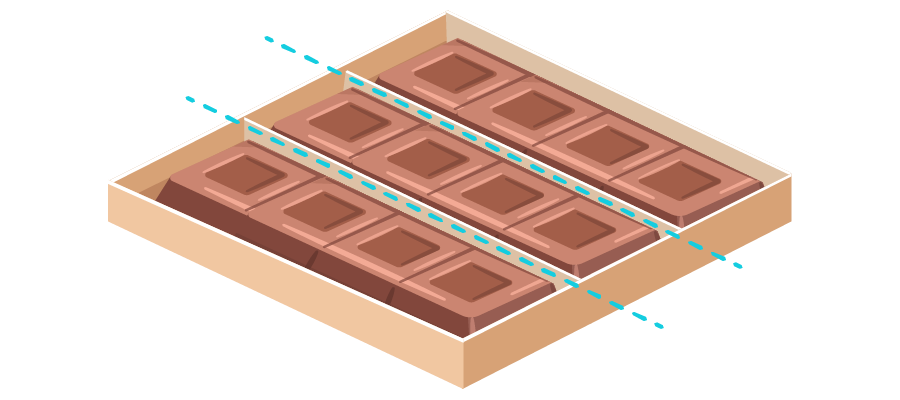
Como nuestra unidad son doce postres, realizamos la división : nos damos cuenta que si partimos la caja de doce, en tres partes iguales, cada parte estará compuesta por cuatro postres. El dos en el numerador de , indica que el primer niño debe tomar dos de esas tres partes, como cada parte es de cuatro, se quedará con postres. Puedes notar ahora por qué se afirma que los números que están en el numerador multiplican.
Conocer el número de postres que le corresponden al segundo niño es ahora muy sencillo. Ya hemos dividido nuestra unidad, postres, en tres partes iguales. El uno en la fracción , nos dice que solo le corresponde una de esas partes; así, al segundo niño le corresponden los cuatro postres restantes.
Aunque en páginas siguientes explicaremos la suma de fracciones, este es el momento oportuno para hacer la siguiente observación: nota que de la unión de y de la caja, se conformo la totalidad. En términos de operaciones esto quiere decir que . En esta ocasión el símbolo no representa solo una unidad como se acostumbra. Está representando la totalidad que estamos dividiendo, la caja de doce postres.

Las fracciones también se pueden utilizar para establecer una relación numérica entre las partes y el todo, observa:
Paula debe responder un examen que consta de preguntas. Si de las preguntas Paula contesta , ¿qué fracción de la prueba respondió?
En estos casos entenderemos la barra horizontal de la expresión como la palabra “de”. Entonces la expresión puede ser leída como “ unidades de en total”. Como Paula respondió preguntas de un total de , podemos decir: “trece de veinte”, o lo que es igual: . Observa otro ejemplo:
En un salón de clases hay estudiantes de los cuales son niños y son niñas, ¿con que fracciones del total podemos representar los niños y las niñas que hay en el salón?
Hay niños de estudiantes, por lo tanto la fracción del total que los representa es . Análogamente se tiene que del total son niñas.
/es/fraccionarios/como-se-leen-las-fracciones/content/