Os números decimais
Relação de ordem com números decimais


/pt/os-numeros-decimais/tipos-de-numeros-decimais/content/
Estabelecer relações de ordem entre os números é determinar qual deles é maior e qual é menor. Já sabemos como estabelecer relações de ordem entre números naturais, inteiros e racionais. Agora veremos como fazer isso com os decimais.
Primeiro, consideramos os valores posicionais inteiros, isto é, as unidades, dezenas, centenas, etc. Depois os valores posicionais decimais: os décimos, centésimos, milésimos, etc. Usaremos os números e como exemplo.
Começamos comparando cada valor posicional da esquerda para a direita. Isto significa que a prioridade está sendo dada aos mais significativos: aqueles que representam o maior número de unidades.
Neste caso, há um número um na posição das dezenas do primeiro número e zero nas dezenas do segundo. Podemos afirmar imediatamente que o primeiro é maior:
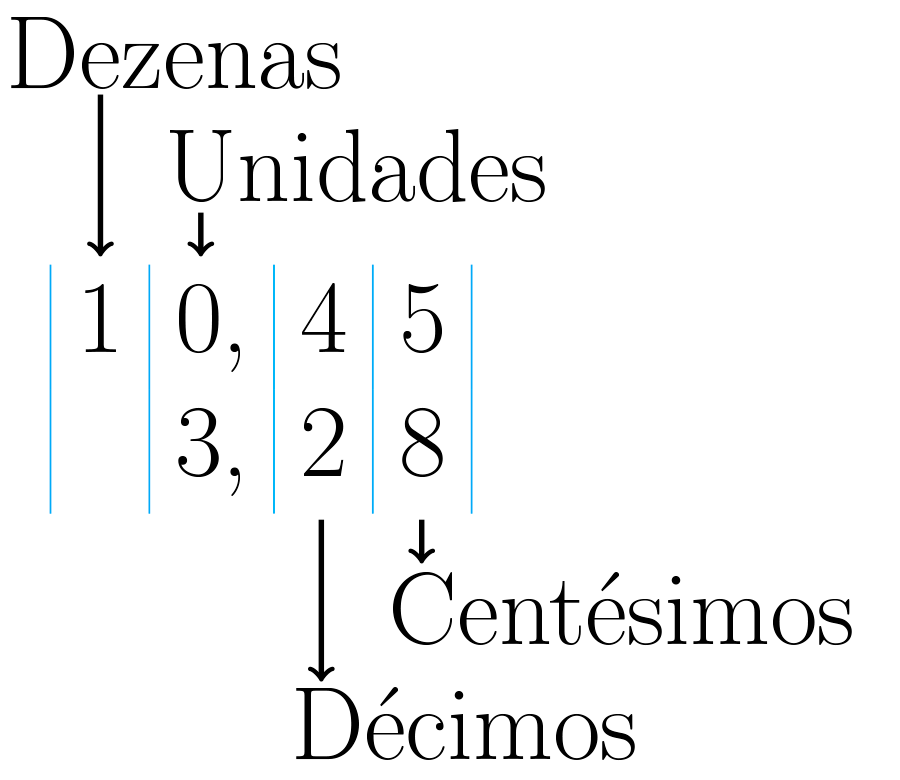
Comparamos os números e
Novamente devemos começar da esquerda para a direita. Neste caso, os dois números começam nas unidades: cada um tem dois. Como este valor posicional não determinou qual é o maior, continuamos com o próximo à esquerda.
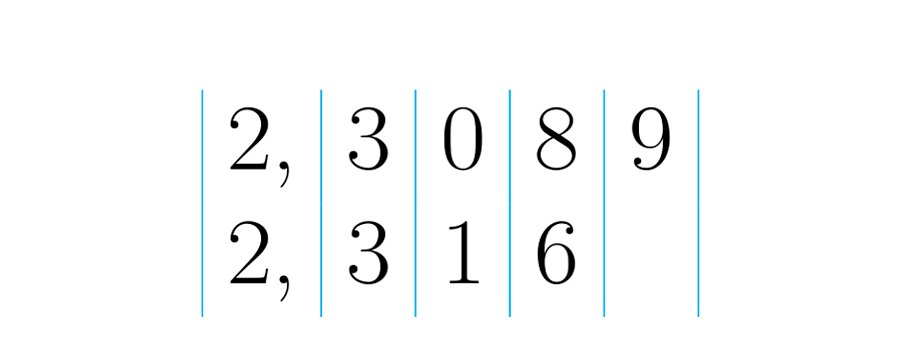
Os centésimos: o primeiro número tem zero centésimos e o segundo um. Podemos dizer então que o segundo número é maior que o primeiro: .
Observe que embora a parte decimal do primeiro número, pareça ser maior que a segunda, isto não significa que seja maior que Não se deixe confundir pelas aparências.

Observe que ao representar esses números na reta, o menor está à esquerda do maior. Isto está de acordo com as explicações feitas sobre a ordem na reta numérica.
/pt/os-numeros-decimais/converter-fracao-em-decimal-com-resultado-exato/content/