/pt/os-numeros/algumas-propriedades-do-conjunto-dos-numeros-racionais/content/

Ordem no conjunto dos números racionais

Os números racionais também representam quantidades, de modo que alguns podem representar mais do que outros, ou seja, existe uma relação de ordem entre eles. Vejamos como determinar quando um número fracionário é maior do que o outro.

Suponhamos que vamos comparar os números   e , isso é equivalente a responder à pergunta: o que é maior, cada uma das partes que ficam quando dividimos 5 unidades por nove partes, ou o que obtido da divisão de quatro por sete? Observe:

Passo 1:

Devemos colocar as frações uma ao lado da outra.

Passo 2:

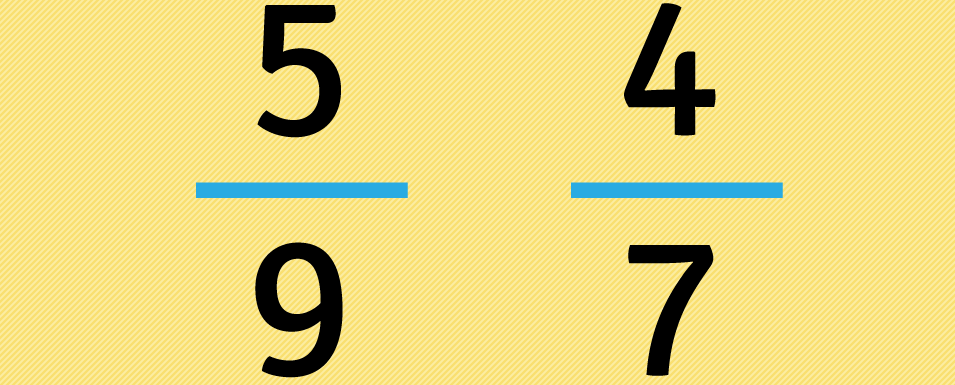
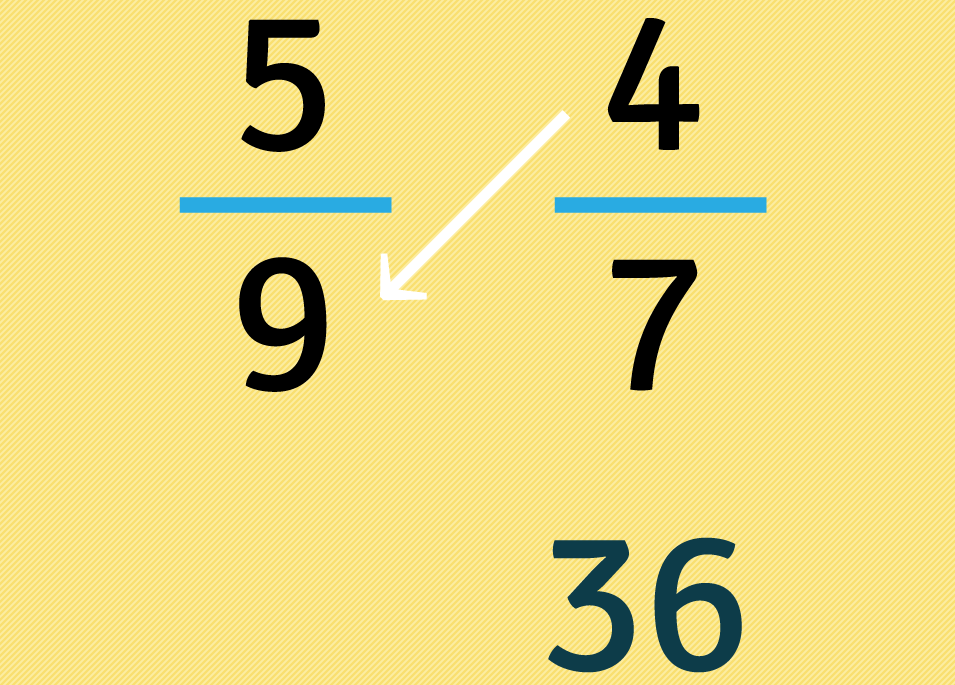
Independentemente dos sinais de menos (-), que podem ter, multiplicamos o numerador da primeira fração pelo denominador da segunda e colocamos o resultado da multiplicação embaixo da primeira fração.

Passo 3:

Mais uma vez, sem considerar o , multiplicamos o numerador da segunda fração pelo denominador da primeiro, colocamos este resultado embaixo da segunda fração.

Passo 4:

Colocamos entre as frações o símbolo de ordem entre as multiplicações feitas. Neste caso, como é inferior a , colocamos o símbolo entre eles.

Passo 5:

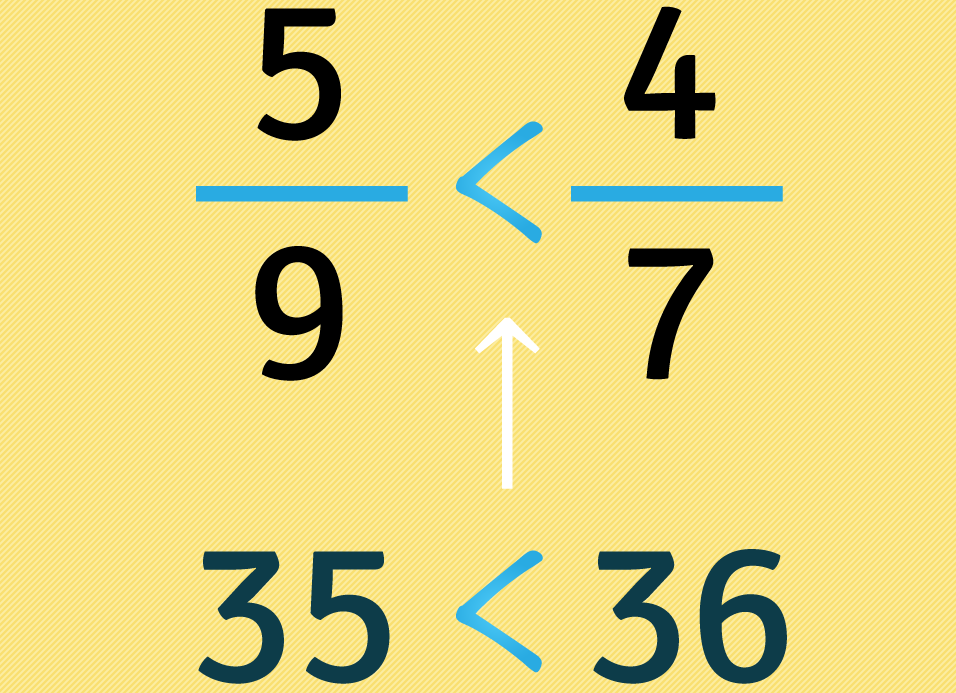
Cada número negativo que tivermos na fração fica do lado maior, mudamos o sentido do sinal ou que colocamos. Neste caso, quando não tem nenhum sinal (-) no número , deixamos o símbolo como está.

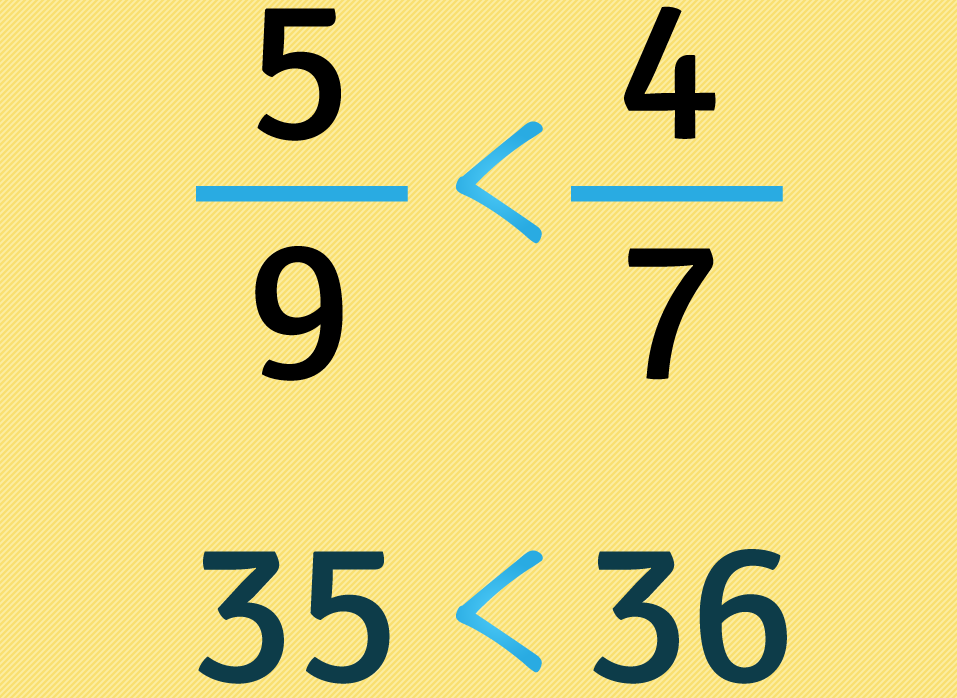
Podemos concluir que representa mais, ou é maior, que : .  

Vejamos outro exemplo, vamos comparar os racionares e :

Passo 1:

Posicionamos as frações uma ao lado da outra.

Passo 2:

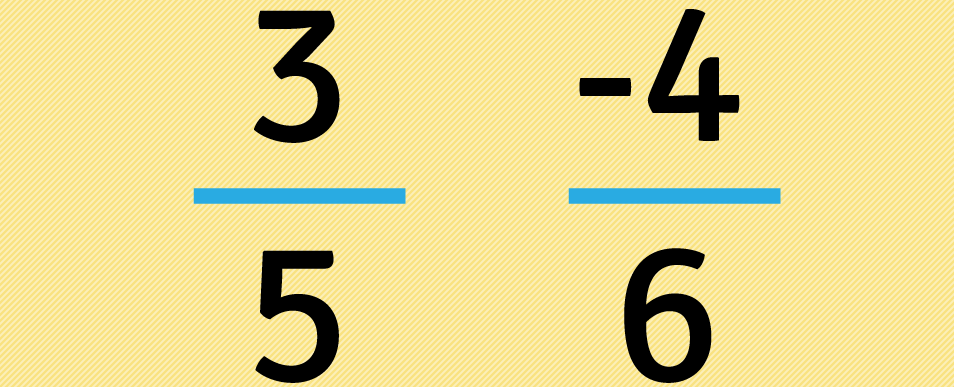
Sem considerar o sinal , multiplicamos três por seis: , em seguida colocamos o resultado da multiplicação embaixo da primeira fração.

Passo 3:

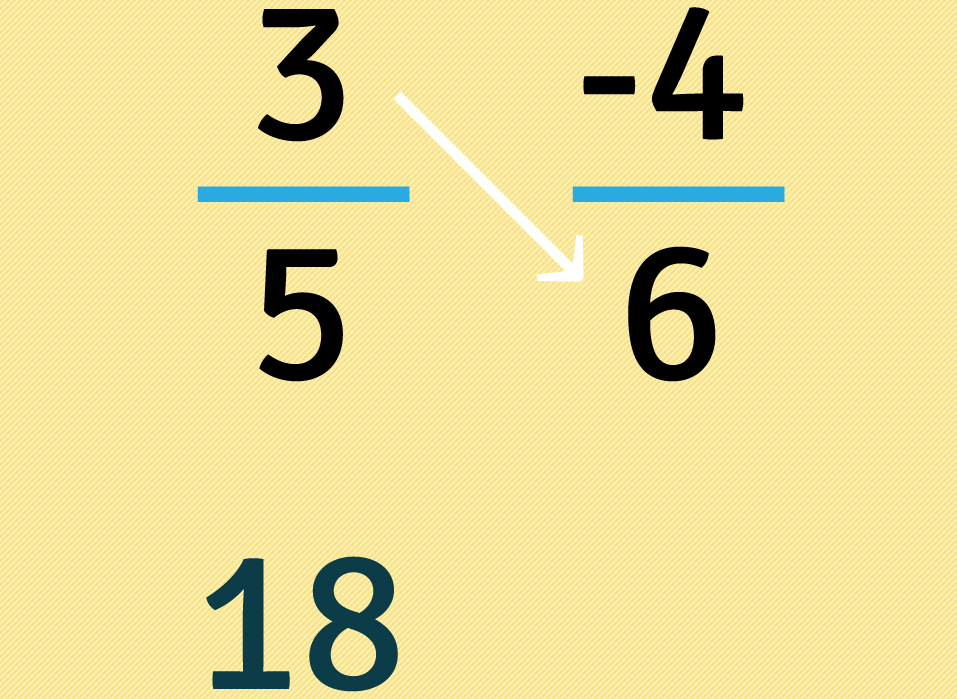
Agora multiplicamos quatro por cinco: , depois colocamos este resultado embaixo da segunda fração.

Passo 4:

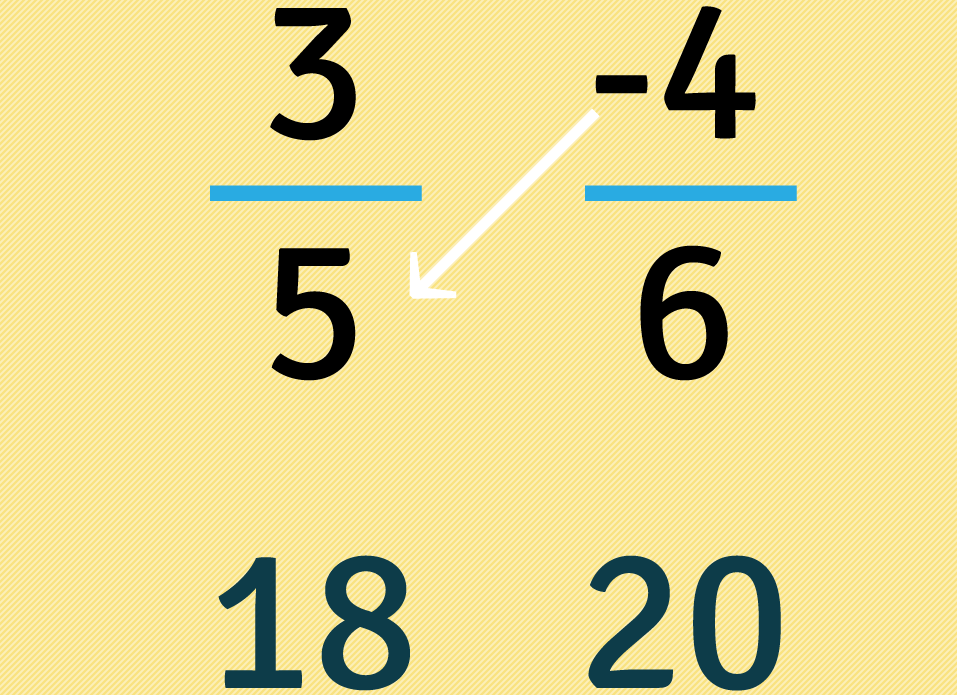
Como dezoito é inferior a vinte, devemos usar o sinal menor do que assim: . Em seguida colocamos o mesmo sinal entre frações:  

Passo 5:

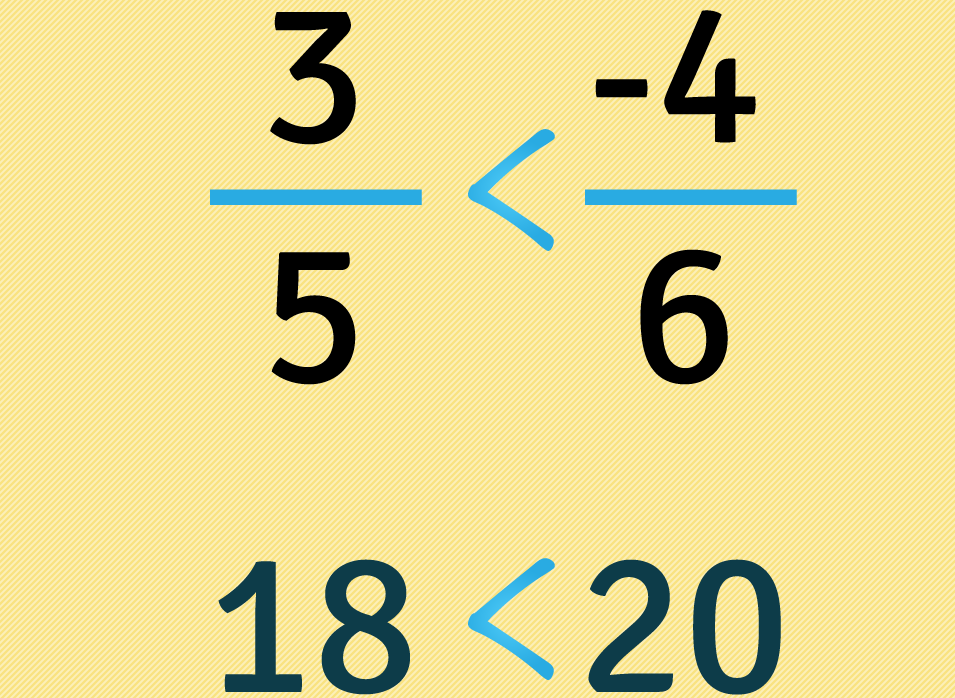
Como existe um sinal de - (menos) na fração que ficou do lado maior   , vamos mudar o sentido do sinal   uma vez, pomos agora entre as frações.

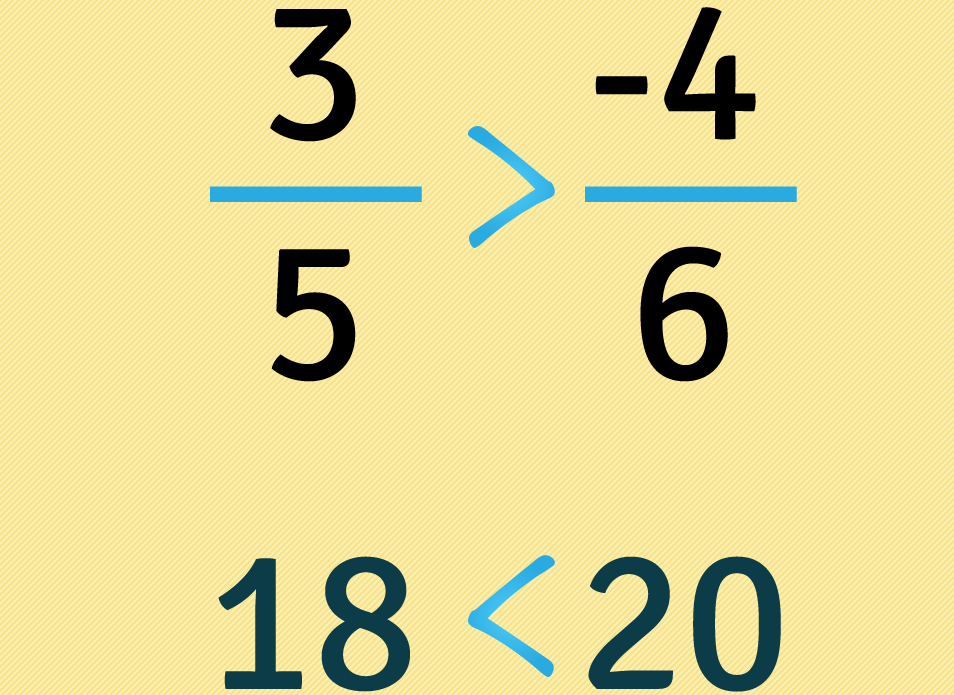
Podemos concluir que é maior que . Isto já era de se esperar porque os números negativos representam dívidas e os positivos pertences. Agora a melhor coisa a fazer é praticar para fixar o aprendido.

/pt/os-numeros/aprendendo-a-contar/content/