Números Fracionários: As proporções

Página 22: As proporções

/pt/numeros-fracionarios/as-taxas/content/

As proporções

Os conceitos de razão e proporção estão diretamente ligados, inclusive em muitas ocasiões é fácil confundí-los. Saiba quais são suas diferenças e como são usados para resolver problemas.

Uma proporção é definida como a igualdade de duas razões. A razão entre e é a mesma que entre e por isso escrevemos:

Dizemos então que esses números são proporcionais. A proporcionalidade também é entendida como uma espécie de analogia matemática, expressando que está para como está para

Exemplo 1:

Andrea e Márcio contribuem com e respectivamente, juntando que é o preço de um pacote de balas. Como essas balas devem ser distribuídos para que cada um tenha proporção que contribuíram?

Primeiro, vamos calcular a razão entre os valores que Andrea e Martin pagaram, e para isso simplificamos:

A razão é de três para dois, e isso significa que para cada três centavos que Andrea contribuiu, o Márcio colocou dois. Desta forma, as balas devem ser distribuídas da mesma maneira. Portanto, a distribuição das balas deve ser para Andrea e para o Márcio. Assim, ao calcular a razão entre as balas que recebem, perceberemos que Portanto as contribuições e as balas recebidas por cada tem uma proporção:

Observe que para cada duas balas que Márcio recebe, Andrea recebe três:

Exemplo 2:

Agora veja como encontrar números proporcionais. Vamos resolver a seguinte questão: está para assim com quem está para ?

Para começar, vamos traduzir essa questão para o idioma das proporções. Usando o símbolo para representar o número pesquisado, podemos escrever que está para como está para :

O procedimento é o seguinte: observe que há um número que acompanha o no mesmo lado do igual, o quinze, que está dividindo (no denominador). Portanto, ele deve ser transferido para o outro lado do igual (para a esquerda), mas executando a operação oposta, isto é, multiplicando.

Passa para o outro lado do igual para realizar a operação oposta.

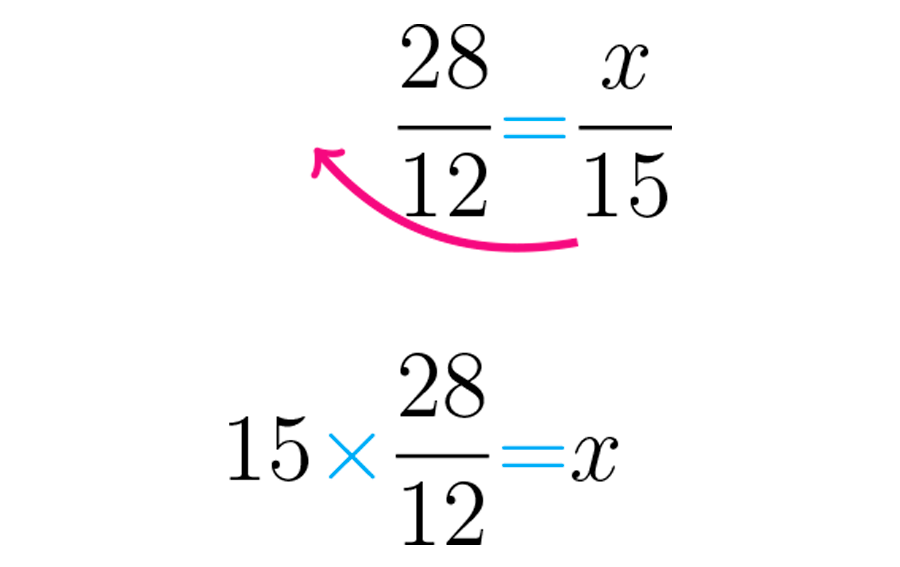
Quando você efetua a operação , obtém a resposta: Isso significa que está para assim como está para :

Se acontecer do símbolo estar no denominador, simplesmente invertemos as duas frações e procedemos como acabamos de ver:

Exemplo 3:

Uma lebre e uma tartaruga estão competindo numa corrida e, para cada metros que a tartaruga corre, a lebre corre . Se a tartaruga correr metros, quantos metros correrá a lebre?

As distâncias percorridas pela tartaruga e a lebre estão na razão de para : . Tanto o que a tartaruga avança assim como a distância que a lebre corre deve respeitar sempre a mesma razão. Portanto, se chamarmos a distância que corre a lebre, quando a tartaruga correr teremos:

Como o símbolo está num denominador, invertemos as duas frações obtendo a expressão mostrada na figura abaixo.

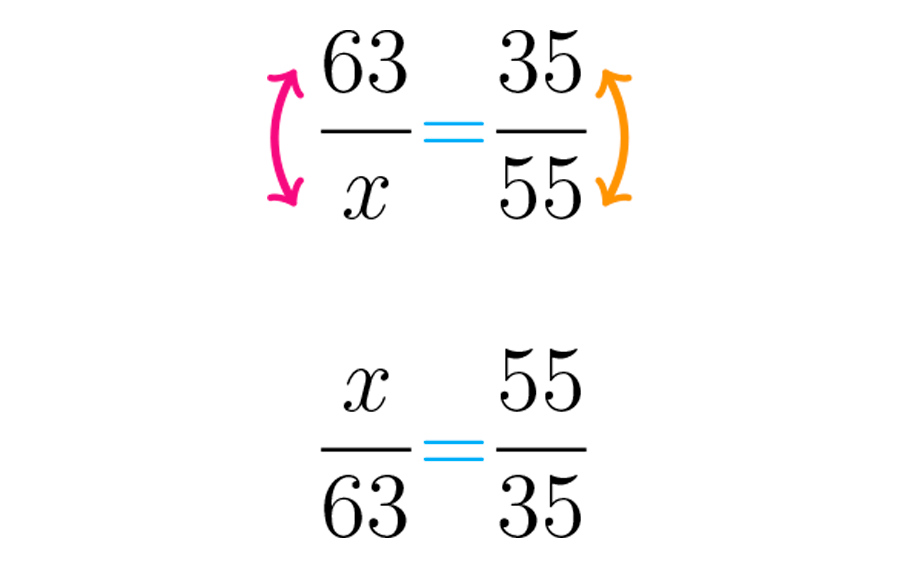
Agora podemos prosseguir como no exemplo anterior, posicionando o . Isto é, deixando-o sozinho ao lado do igual.

Passamos o número que acompanha o para o outro lado do mesmo, mas fazendo a operação oposta. Assim, obtemos a expressão Ao realizar a operação indicada, o resultado é obtido, Portanto, se a tartaruga corre , a lebre corre .

Existe uma proporção interessante que está presente na arte, biologia e até mesmo determina na formação de alguns furacões e galáxias: a proporção áurea. Acredite ou não, seu corpo, as plantas, os animais e todo o universo estão cheios de conceitos matemáticos.