Los decimales
Decimales periódicos mixtos a fracción


/es/los-decimales/decimales-periodicos-puros-a-fraccion/content/
Tal vez el siguiente método te parezca un poco complicado pero es muy efectivo. Con seguridad, cuando aprendas más conceptos matemáticos, comprenderás por qué este es así. Por ahora te recomendamos practicarlo.
Observa el siguiente ejemplo: el decimal periódico mixto
Se escribe el número en su notación simplificada con la barra: .
El numerador será el decimal completo: , menos la parte entera seguida de la parte decimal que no se repite: . Todo escrito sin comas ni barras:
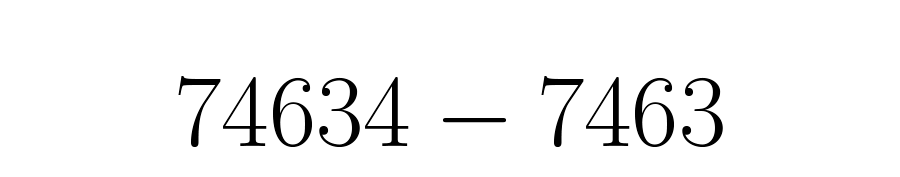
El denominador será tantos nueves como cifras tenga la parte que se repite periódicamente, seguidos de tantos ceros como tenga la parte decimal que no se repite.
En este caso solo hay una cifra que se repite periódicamente, el por lo tanto habrá solo un nueve. La parte decimal que no se repite tiene dos cifras: y , por lo tanto el nueve va seguido de dos ceros.
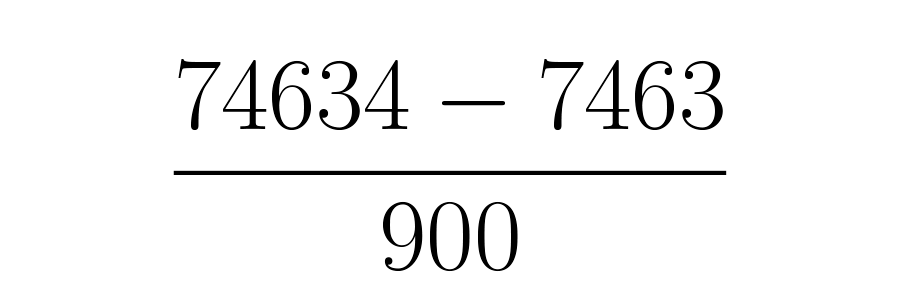
Ahora se debe realizar la resta . Al obtener la fracción se procede a simplificar. Si esta es irreducible, como en este caso, se deja como está:
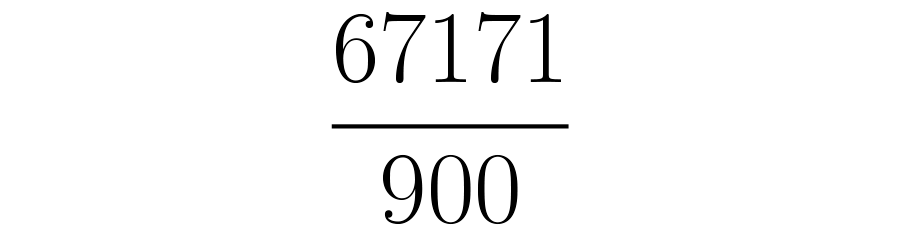
El resultado anterior quiere decir que . Si quieres comprobarlo, realiza la división , te darás cuenta que da como resultado
Se escribe el decimal en notación simplificada: .
El numerador será el decimal completo: , menos la parte entera seguida de la parte decimal que no se repite: . Todo escrito sin comas ni barras:
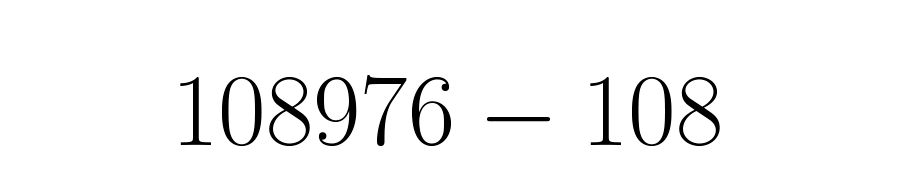
Como la parte periódica tiene tres cifras: y , ponemos tres nueves en el denominador, seguidos de dos ceros, pues hay dos decimales que no se repiten: el y el .
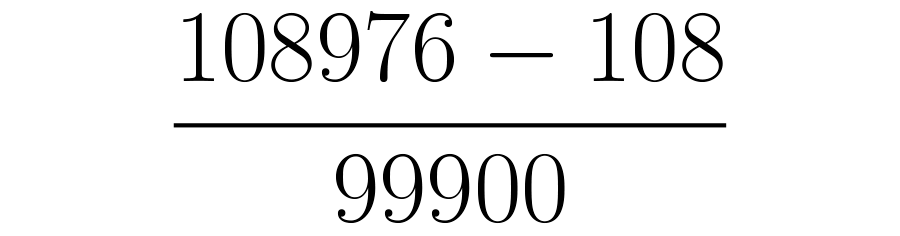
Realiza la resta así obtendrás en el numerador. Posteriormente se simplifica la fracción resultante. En esta ocasión es posible simplificar por cuatro. El resultado anterior quiere decir que .
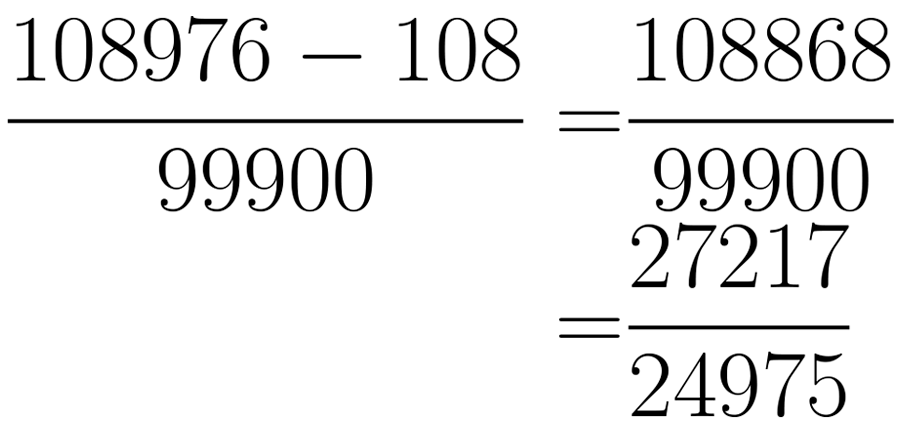
Si realizas la división , te darás cuenta de que su resultado es precisamente .
/es/los-decimales/decimales-infinitos-no-periodicos-a-fraccion/content/