Fraccionarios
Simplificación de fracciones


/es/fraccionarios/amplificacion-de-fracciones/content/
Simplificar fracciones te ayudará a realizar operaciones más fácilmente, aprende a hacerlo aquí.
Observa la siguiente situación: cierta pizzería vende porciones personales de un doceavo de pizza. Ana, que va a comprar para sus amigos, necesita quince porciones. Sin embargo en el restaurante, que tiene una nueva administración, ahora las porciones son de un cuarto de pizza. ¿Cuántas porciones debe pedir Ana si quiere llevar la misma cantidad?
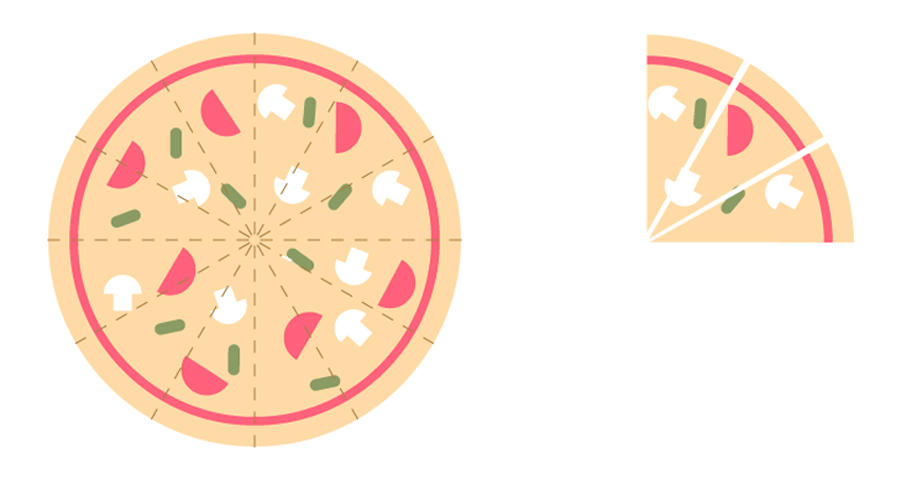
Para saber cuántas porciones debe llevar, Ana necesita encontrar una fracción equivalente: como cada porción es de un doceavo, y ella desea quince, la fracción de pizza que quiere llevar es quince doceavos: . Ahora bien, las nuevas porciones son de un cuarto de pizza, así que la fracción de pizza que lleve tendrá denominador cuatro: . Necesita encontrar un número tal que:
Observa que para transformar el denominador doce en cuatro, se dividió en tres. Así que para encontrar el nuevo numerador se debe hacer lo mismo, dividir el antiguo en tres: . Si Ana lleva porciones, puede estar segura de que llevará la misma cantidad de pizza que necesita porque:
Siempre que en una fracción, dividas numerador y denominador por el mismo número, obtendrás una fracción equivalente. A este proceso se le conoce como simplificación.
Fíjate que para poder dividir el numerador y el denominador por el mismo número, este tiene que ser divisor común de los dos. Por esta razón el proceso de simplificar se detiene cuando los números son primos relativos, o sea, cuando no tienen más divisores comunes que . Cuando esto pasa, es decir, cuando una fracción no se puede simplificar más, se dice que es irreducible.
Dada una fracción, podemos simplificar reiteradamente hasta obtener una fracción equivalente irreducible. El truco es dividir una y otra vez por los números primos, observa: simplifiquemos llevándola a su fracción equivalente más simple:
Si se quiere llevar a su mínima expresión una fracción en un solo paso, se debe dividir por el máximo común divisor. En el ejemplo anterior así:
Observa que la descomposición prima de es que son precisamente los números por los que dividimos en el procedimiento anterior.
Recuerda que los números que están en el numerador multiplican, mientras que los están en el denominador dividen. Podemos usar el hecho que la multiplicación y la división son operaciones opuestas para simplificar por otro método.
¿Qué pasa si multiplicas un número por dos y después lo divides por dos? La respuesta es que el número original no se afecta, por ejemplo: tomemos el número seis, si primero multiplicamos por dos obtenemos: si luego dividimos este resultado en dos: ¡Podemos hacer de cuenta entonces que el dos multiplicando se cancela con el que está dividiendo y solo queda el Ahora observa como podemos usar esto para simplificar:
Las descomposiciones primas de y son y respectivamente, por lo tanto:
Fíjate que un dos, dos tres y el siete están al tiempo multiplicando y dividiendo (arriba y abajo), por lo tanto podemos cancelarlos:
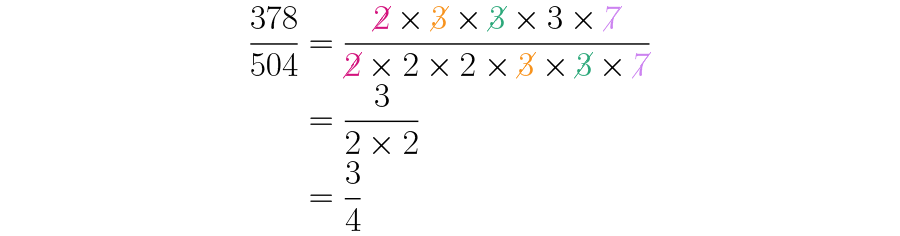
Así llegamos rápidamente a la fracción equivalente más simple de
/es/fraccionarios/numeros-mixtos/content/