/es/fraccionarios/resta-de-fracciones-heterogeneas/content/
Ahora que sabes sumar y restar cualquier tipo de fracciones puedes usarlas para resolver problemas del día a día, observa:
Un cultivador siembra de su granja con maíz, y con soya. ¿En total qué fracción de la granja sembró?
En el siguiente interactivo puedes ver el procedimiento completo.
Haz clic en los botones y para avanzar y retroceder en el mismo:
Aprovechemos el ejercicio anterior para formular otra pregunta: ¿qué fracción de la granja queda aún sin sembrar?
Para responder debemos restar, a la totalidad de la granja, la fracción que se sembró. Recuerda que la totalidad es representada por la unidad; así, la totalidad de la granja será representa por el número . Debemos entonces realizar la resta .
Para sumar o restar un número entero con una fracción, ponemos un uno como denominador del número entero así: . Recuerda que también que los enteros y naturales tienen fracciones equivalentes.
Después realiza la suma o resta de fracciones como has aprendido:
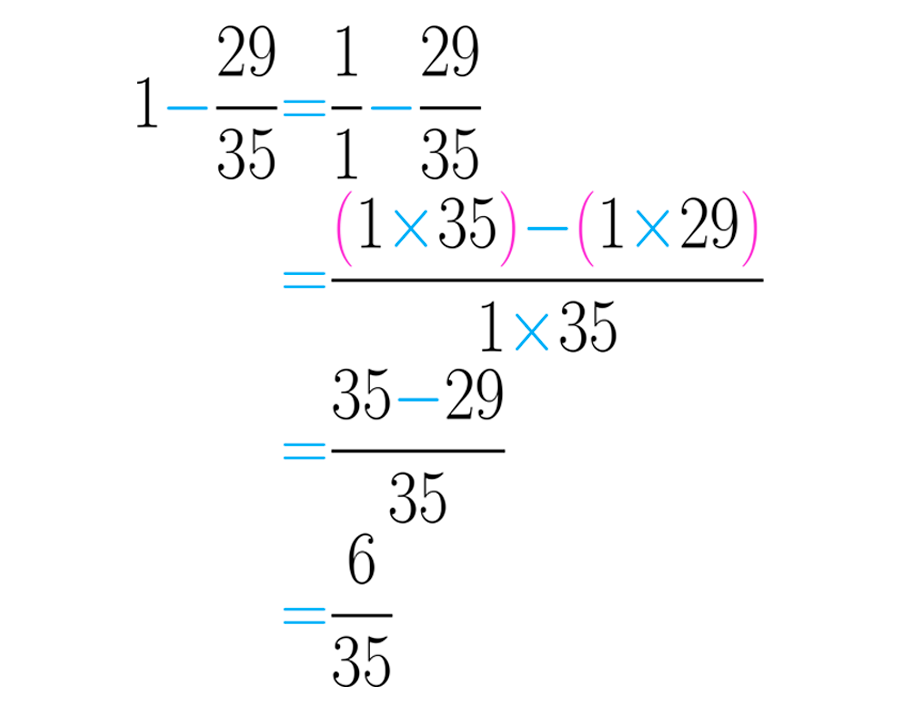
El resultado anterior quiere decir que quedan sin sembrar de la granja.
Un deportista decide entrenar recorriendo cierta pista de atletismo. El primer día recorre de la pista, el segundo y el tercer día . ¿Cuántas vueltas le dio a la pista en total?
Para determinar cuántas vueltas dio en total, debemos sumar los recorridos hechos cada día. En esta ocasión, en lugar de usar la fórmula de la suma, transformaremos las fracciones a unas equivalentes con denominador igual al mínimo común múltiplo de los denominadores, :
Así, obtenemos una suma de fracciones homogéneas que es mucho más fácil de hacer. Ahora solo se deben sumar los numeradores:
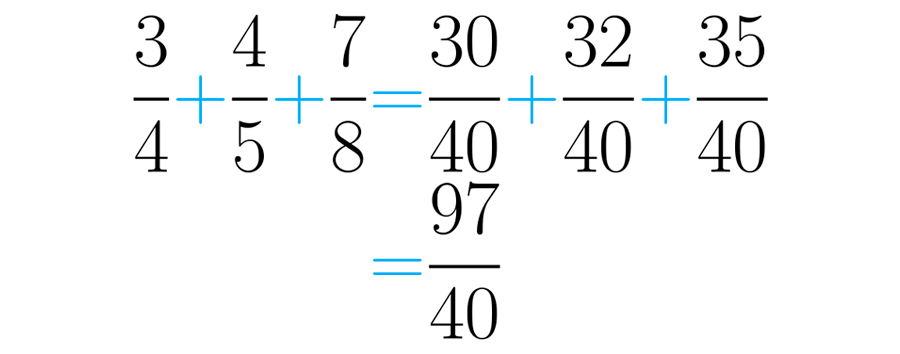
La respuesta es que el deportista dio de vuelta a la pista, sin embargo esto no nos dice mucho. Para obtener una mejor idea de cuántas vueltas son, es posible transformar la fracción impropia a un número mixto.
Para hacerlo, realizamos la división . Recuerda que el cociente será la parte entera del número, mientras que el residuo será el numerador de la parte fraccionaria:
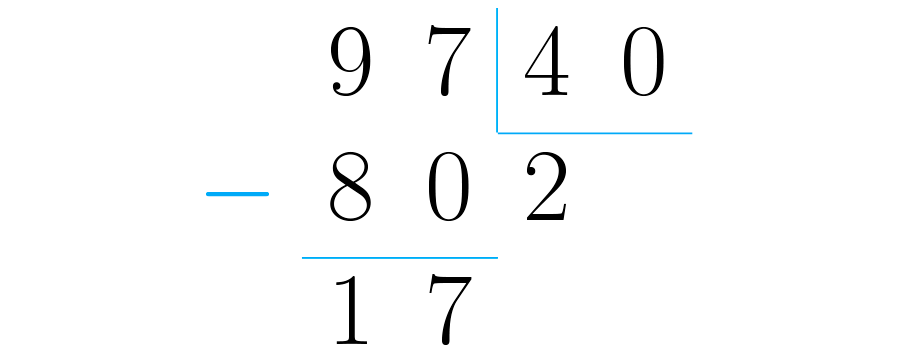
Gracias a la anterior división se puede decir que es lo mismo que . Esto es, el deportista dio dos vueltas, y recorrió de pista más.
/es/fraccionarios/multiplicacion-de-fracciones/content/
