Fraccionarios: Las proporciones

Página 21: Las proporciones

/es/fraccionarios/las-tasas-o-razones-de-cambio/content/

Las proporciones

Los conceptos de razón y proporción están íntimamente ligados, inclusive en muchas ocasiones estos se confunden. Aprende en qué se diferencian y cómo se usan para resolver problemas.

Una proporción se define como la igualdad de dos razones. Por ejemplo, la razón entre y es igual a la que hay entre y escribimos entonces:

Se dice entonces que estas parejas de números son proporcionales. La proporcionalidad también se entiende como una especie de analogía matemática, expresando que es a como es a .

Ejemplo 1:

Andrea y Martín aportan y respectivamente, reuniendo los que cuesta un paquete de golosinas. ¿Cómo deben repartirse las golosinas para que cada uno tenga en proporción a lo que pagó?

Primero calculemos la razón entre lo que pagaron Andrea y Martín, para esto simplificamos:

La razón es de tres a dos, . Esto quiere decir que por cada tres pesos que pagó Andrea, Martín pagó dos. Las golosinas deben distribuirse de la misma manera. Por lo tanto la distribución de los dulces debe ser para Andrea y para Martín. Así, al calcular la razón entre los dulces que reciben nos daremos cuenta que Así los aportes y las golosinas recibidas por cada uno guardan proporción:

Fíjate que por cada dos dulces que recibe Martín, Andrea recibe tres:

Otro ejemplo

Observa ahora como encontrar parejas de números proporcionales. Resolvamos la siguiente pregunta: ¿ es a como quién es a ?

Para comenzar traduzcamos esta pregunta al lenguaje de las proporciones. Usando el símbolo para representar el número buscado podemos escribir es a como es a ”:

Lo que se debe hacer ahora es dejar la sola a un lado del igual, a este procedimiento se le conoce como despejar la incógnita.

La forma de proceder es la siguiente: observa que hay un número acompañando a la al mismo lado del igual, el quince, que está dividiendo (en el denominador). Por lo tanto se debe trasladar al otro lado del igual (a la izquierda), pero efectuando la operación contraria, es decir, multiplicando.

Se pasa al otro lado del igual a realizar la operación contraria

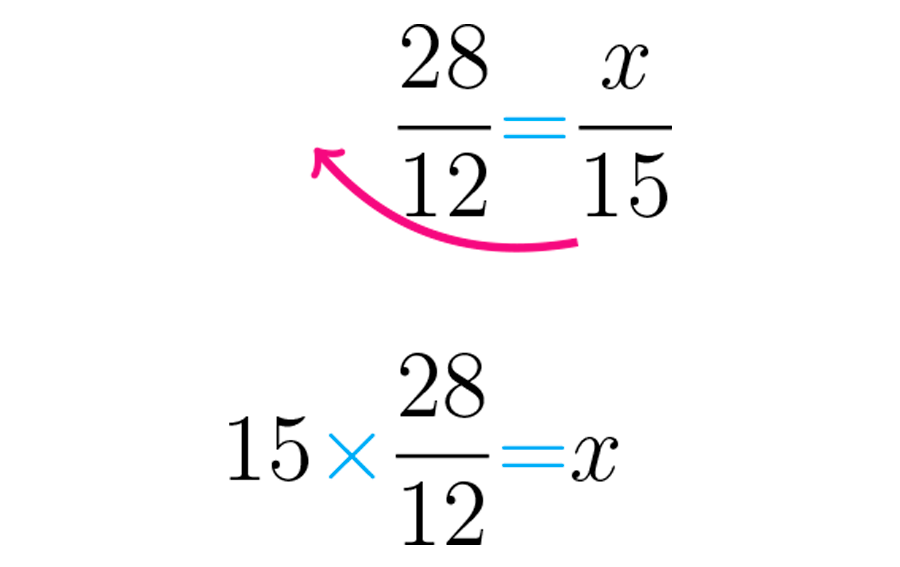
Al realizar la operación se obtiene la respuesta: Esto quiere decir que es a como es a :

Si se da el caso que el símbolo este en un denominador, simplemente invertimos las dos fracciones y procedemos como lo acabamos de ver. Observa:

Otro ejemplo

La liebre y la tortuga están compitiendo en una carrera, por cada metros que recorre la tortuga, la liebre recorre Si la tortuga recorre metros, ¿cuántos la liebre?

Las distancias recorridas por la tortuga y la liebre están en razón de a Lo que avanza la tortuga y la distancia que recorre la liebre siempre deben respetar esta misma razón. Por lo tanto, si llamamos a la distancia que recorre la liebre cuando la tortuga recorre metros tenemos:

Como el símbolo está en un denominador, invertimos las dos fracciones obteniendo la expresión que se muestra en la figura de abajo.

$Se invierten las fracciones$

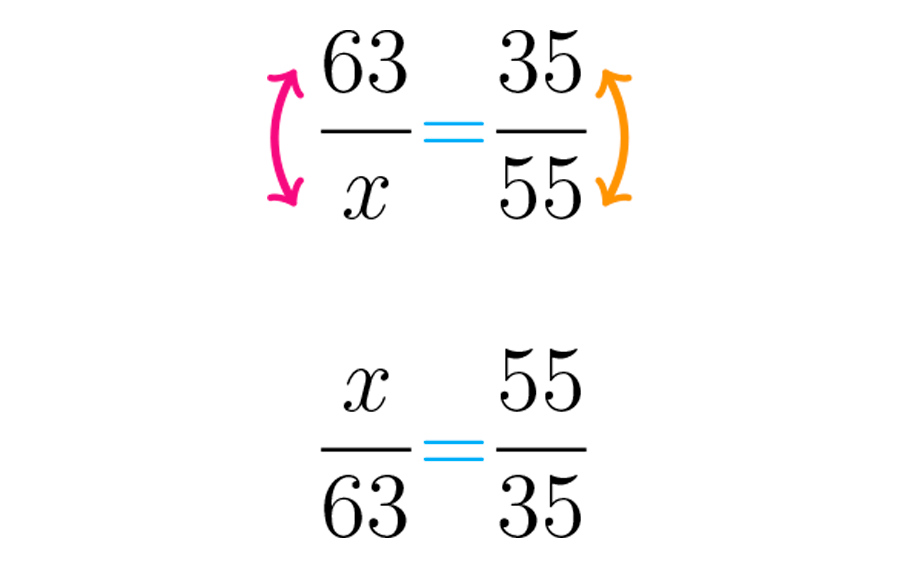
Ahora se puede proceder como en el ejemplo anterior, despejando la Es decir, se deja sola a un lado del igual.

Se pasa el número que está acompañando la al otro lado del igual, pero realizando la operación contraria. Así obtenemos la expresión Al realizar la operación indicada se obtiene el resultado, Por lo tanto, si la tortuga recorre metros, la liebre recorre

Existe una interesante proporción que está presente en el arte, la biología e incluso determina la forma de algunos huracanes y galaxias: la proporción áurea. Aunque no lo creas, el diseño de tu cuerpo, las plantas, los animales y el universo entero están llenos de conceptos matemáticos.