/es/divisores-y-multiplos/propiedades-del-minimo-comun-multiplo/content/
Aquí encontrarás ejemplos resueltos y ejercicios para que pongas en practica los conceptos teóricos.
Observa el siguiente ejemplo: en una estación de bus hay dos rutas, la ruta pasa cada minutos y la ruta cada . Si las rutas coinciden en un momento dado, ¿dentro de cuántos minutos se volverán a encontrar en la estación?
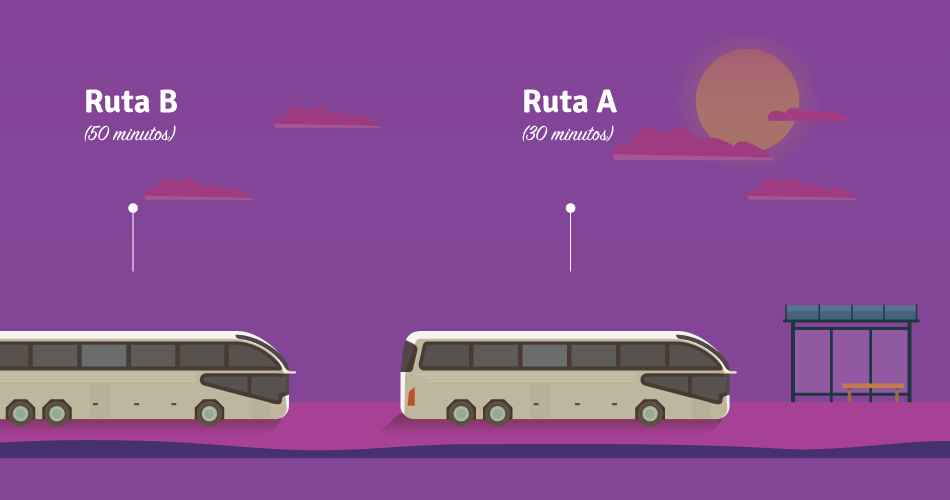
Primero analizaremos el problema para comprender por qué es adecuado el concepto de múltiplo para resolverlo. Piensa en la ruta esta pasa cada minutos. Nota que a partir de un determinado momento, pasará a los , , minutos, etc. Es decir, pasa en los minutos que son múltiplos de . Lo mismo ocurre con la ruta que pasará en los minutos que sean múltiplos de . Luego de comprender esto es fácil ver que las rutas coincidirán justamente en los minutos que sean múltiplos comunes de y .
Para calcular el próximo encuentro de las rutas debemos encontrar el primer múltiplo común diferente de cero: el mínimo común múltiplo. Se procede a descomponer y para calcularlo.
Multiplicando los todos factores primos con su máximo exponente se tiene que . Esto quiere decir que una vez se encuentren en la estación, se volverán a encontrar dentro de minutos.
Dos atletas entrenan recorriendo una pista a la que rodean en y minutos respectivamente. ¿Si parten al mismo tiempo de la línea de salida, cada cuanto tiempo pasan juntos por ese mismo punto?
Realizando el proceso de descomposición se tiene que el de y es el producto . Se puede asegurar que los corredores se encontrarán cada minutos.
/es/divisores-y-multiplos/evaluacion-de-divisores-y-multiplos/content/
