Os conjuntos matemáticos
Operações entre conjuntos


/pt/os-conjuntos-matematicos/relacao-de-igualdade/content/
Além de relacionar os conjuntos através da continência e da igualdade, podemos criar novos conjuntos fazendo operações entre eles, vejamos:
Suponhamos que temos os conjuntos e definidos como na figura abaixo:
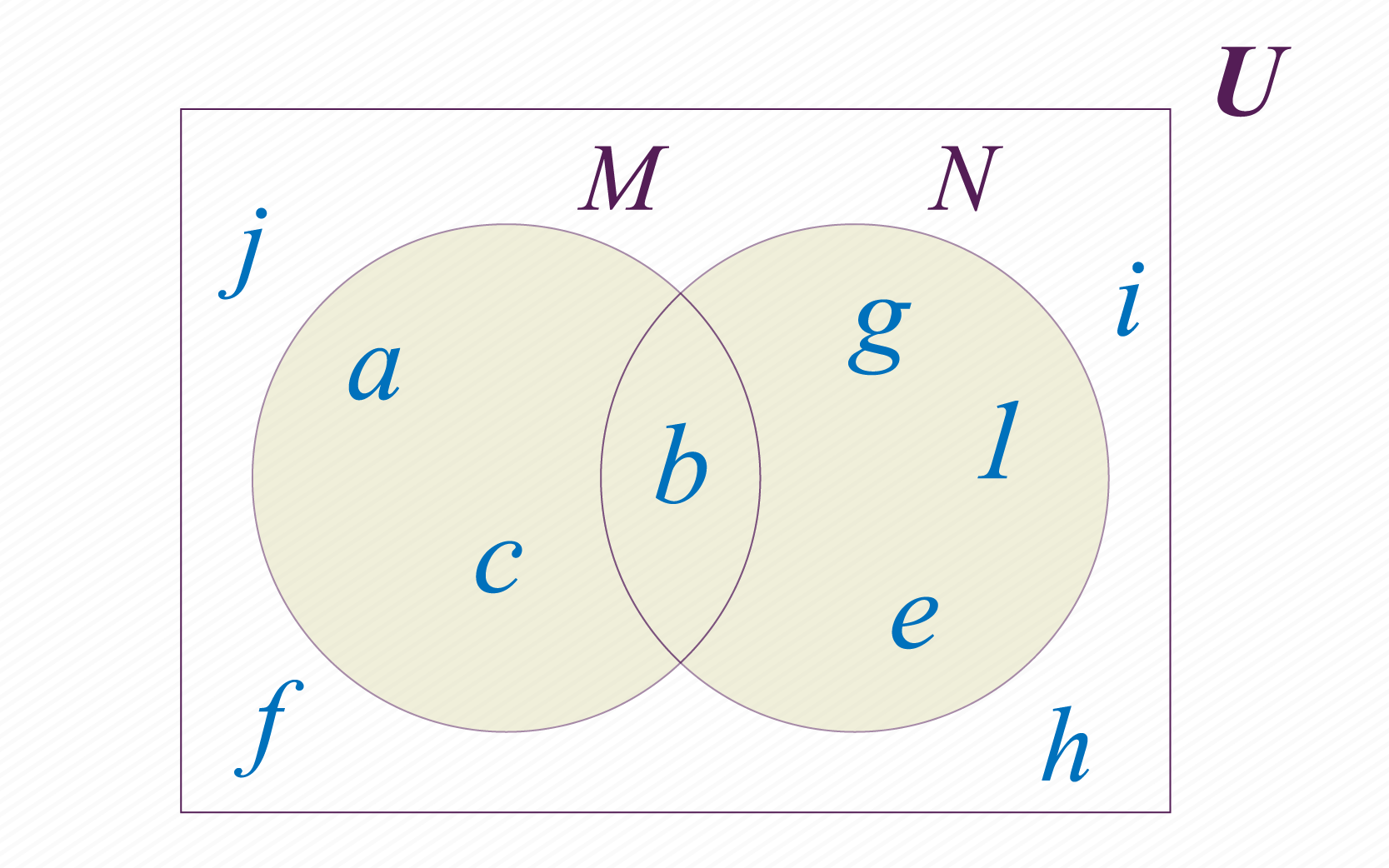
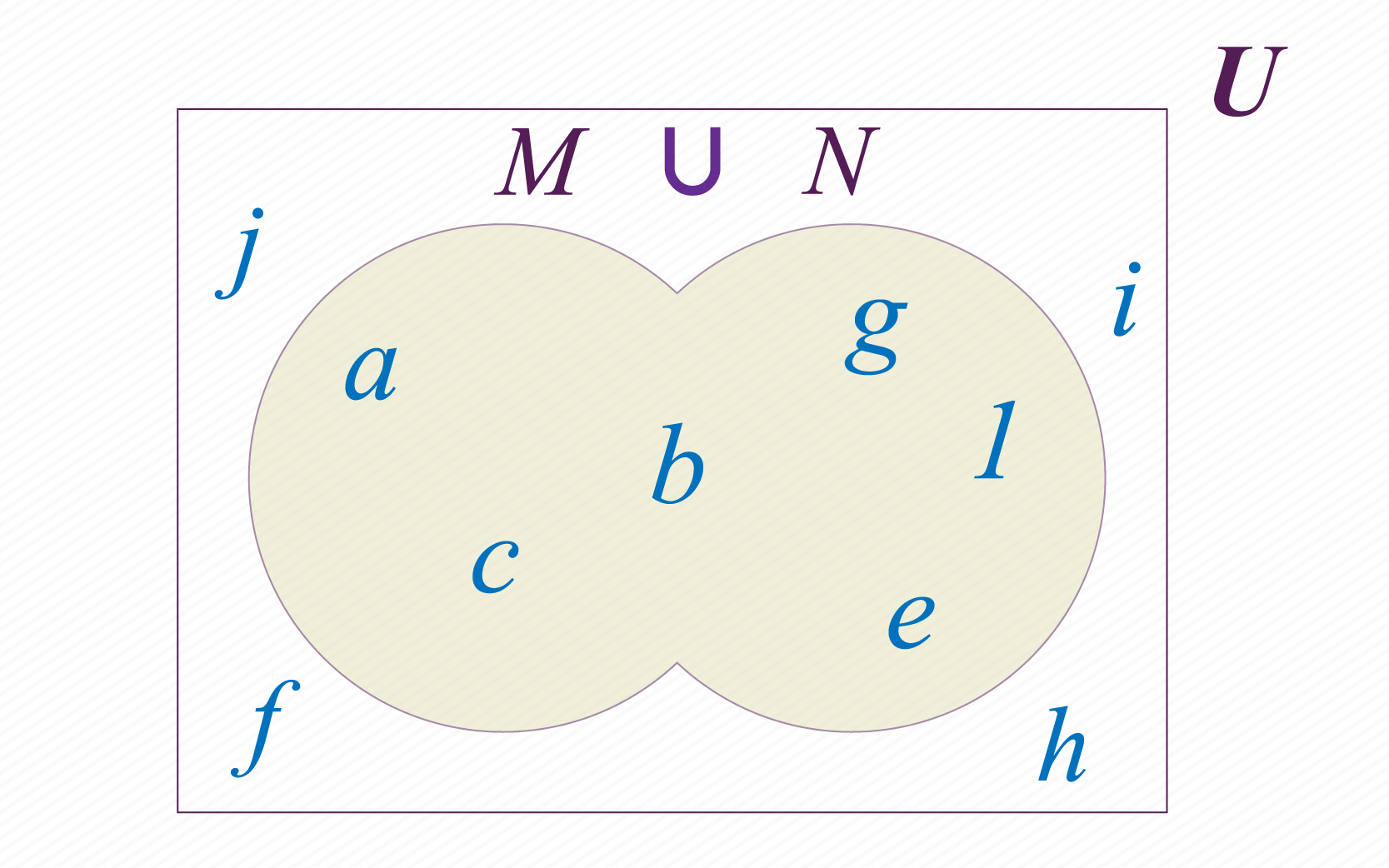
Podemos criar outro conjunto com os elementos que pertencem a ou a . Este novo conjunto será chamado de união de e , e o descrevemos da seguinte maneira: . Na imagem abaixo é possível observar o resultado de união dos conjuntos e .
Ao escolher quais elementos estarão na união dos nossos conjuntos e , devemos nos perguntar quais estão no conjunto “ou” no conjunto . O resultado da operação será o conjunto formado por todos os elementos do conjunto universal , que tem a condição de estar num ou noutro. Temos neste caso:
Continuamos com o exemplo dos conjuntos e definidos anteriormente. Podemos formar um novo conjunto com os elementos que os nossos conjuntos e têm em comum. Este novo conjunto chamaremos de intersecção de e que escrevemos da seguinte forma: .
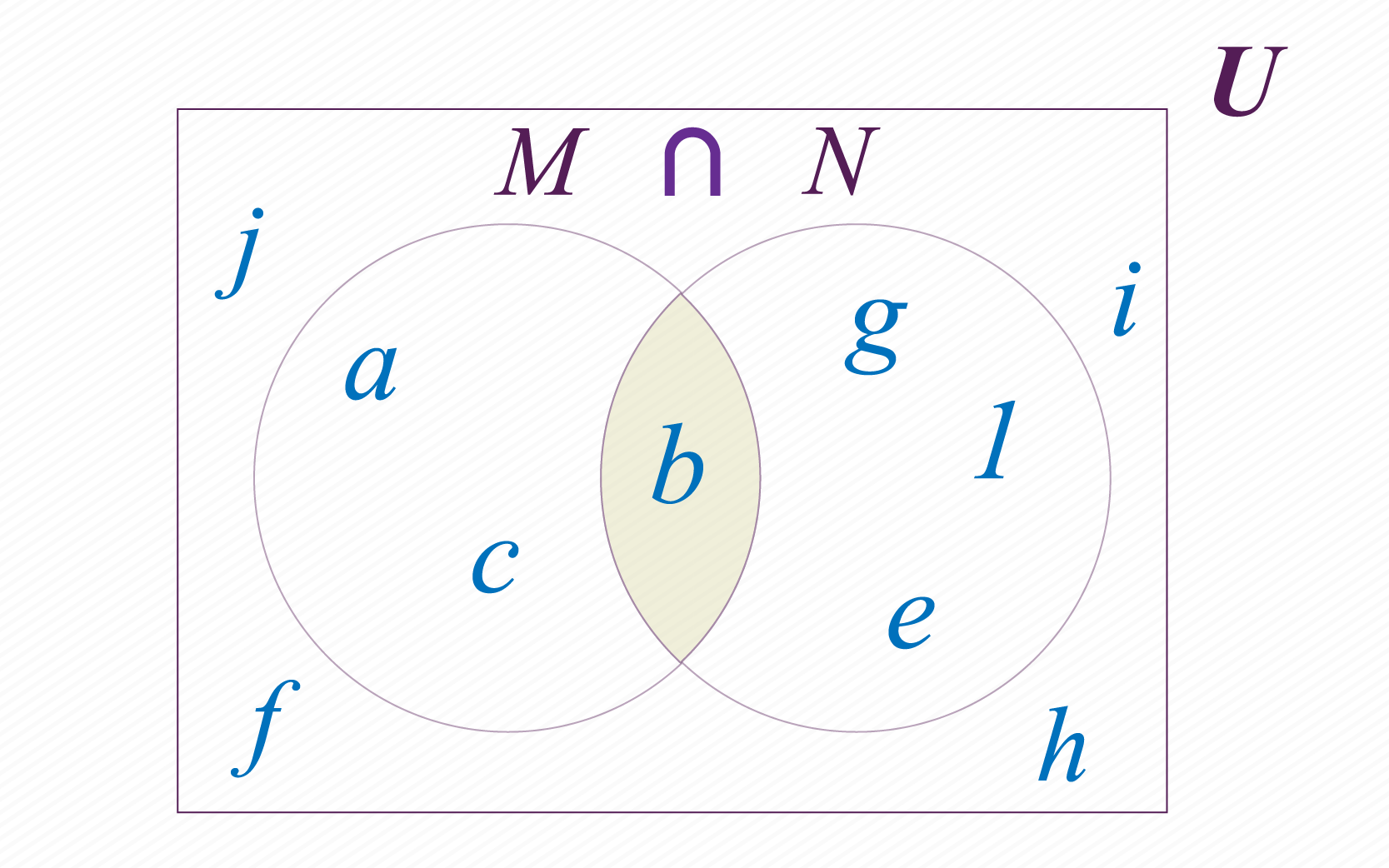
Para determinar quais elementos pertencem a intersecção dos conjuntos e , podemos perguntar quais elementos estão em “e” em . Todos os elementos do conjunto , que têm esta condição deverão estar no conjunto . Na figura acima podemos ver a intersecção de nossos conjuntos e , onde .
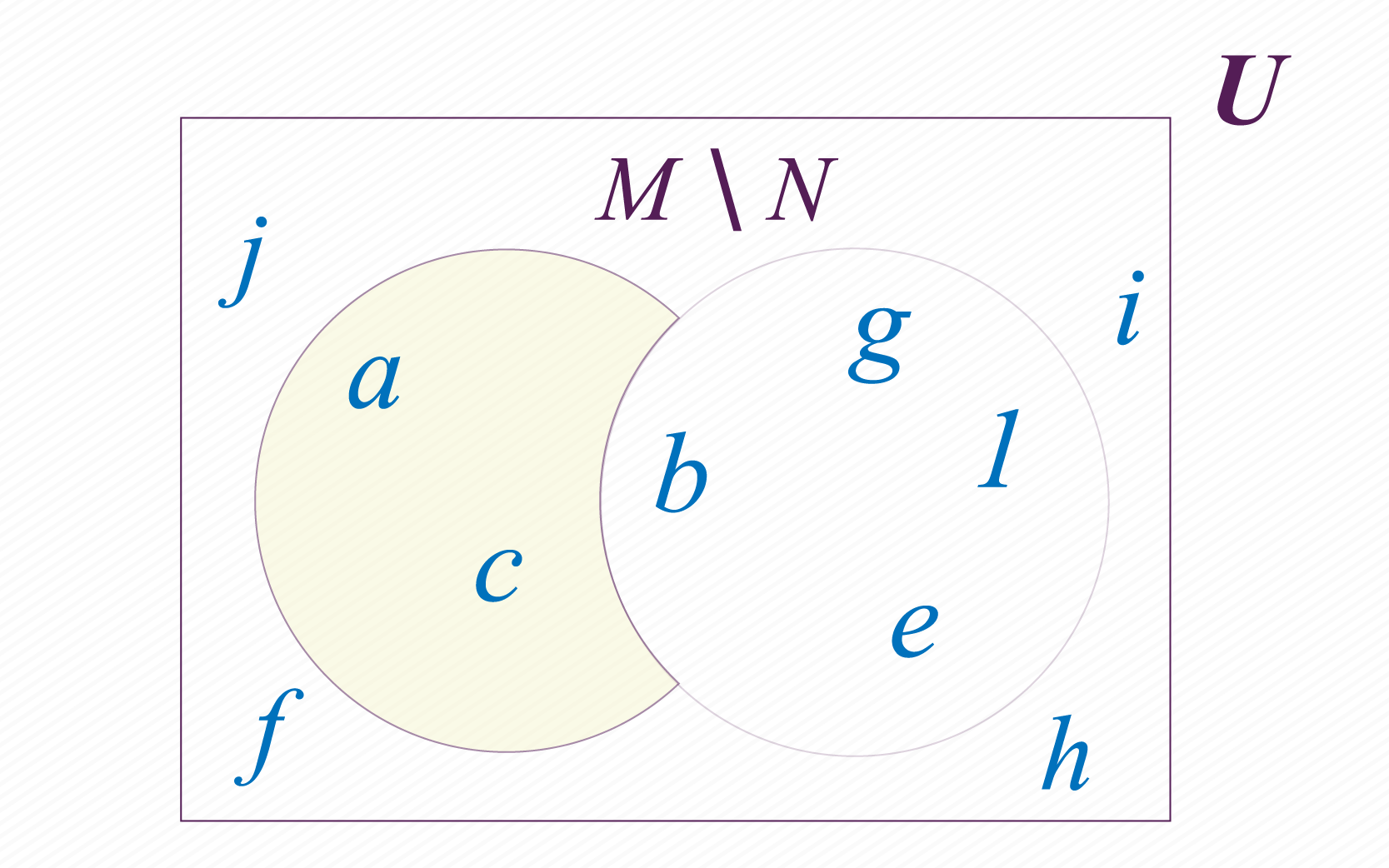
Além da união e intersecção, podemos realizar a diferença de conjuntos. Neste caso devemos selecionar os elementos de um conjunto que não estejam no outro. Por exemplo, se realizamos a operação menos , selecionamos os elementos de que não estão em . Representamos a diferença menos assim: . Observe que neste caso .
Esta operação também é muito simples. Basta escolher os elementos de que não estão em , e os elementos de que não estão em . Podemos ver o resultado da diferença simétrica entre e na figura abaixo. Representamos a diferença simétrica através do símbolo . No caso dos nossos conjuntos e temos: .
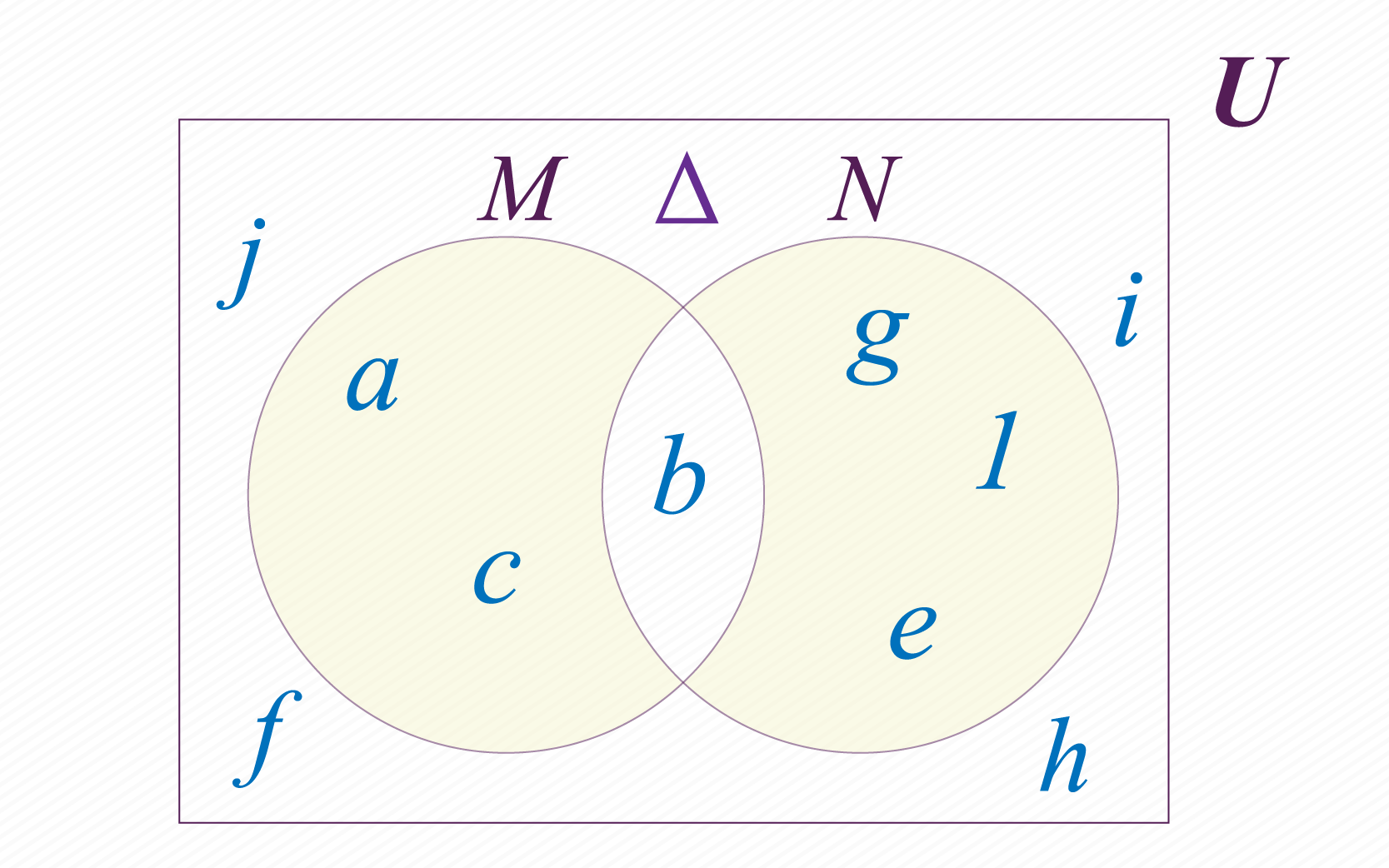
Esta última operação não é entre conjuntos, neste caso é o complemento de um conjunto. Dizemos que o complemento de é o conjunto formado por todos os elementos do conjunto universal , que não pertencem ao conjunto . É comum usar os símbolos , ou para representar o complemento do conjunto , aqui vamos usar o símbolo . Em nosso caso temos e .
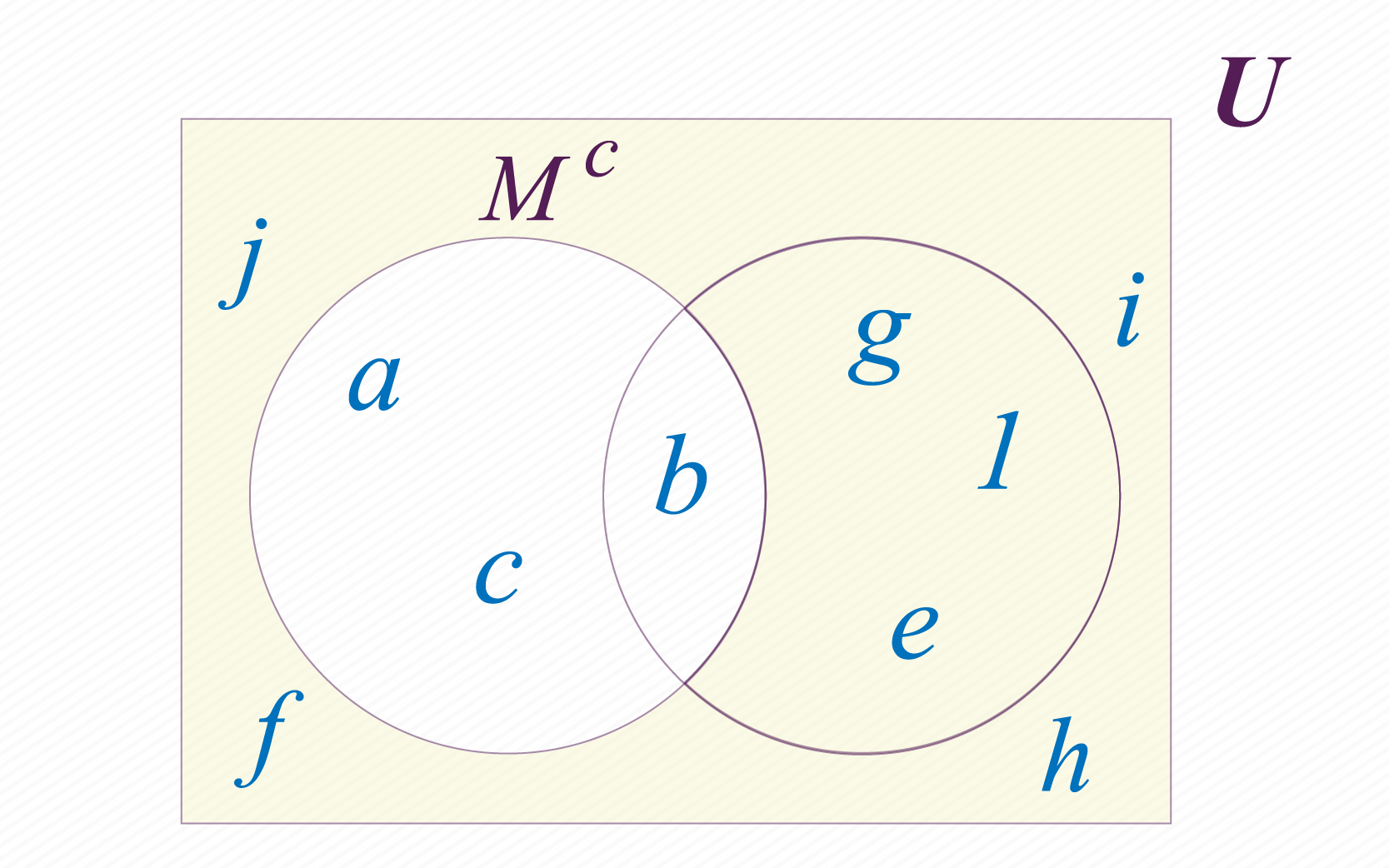
/pt/os-conjuntos-matematicos/situacoes-que-resolvemos-com-os-conjuntos/content/