/pt/divisao/problemas-que-podemos-resolver-com-divisao/content/
As propriedades das operações são ferramentas úteis, e se você não souber como usá-las pode cometer erros. Saiba quais propriedades podem ou não ser usadas na divisão.
Comutar significa trocar uma coisa por outra. A Propriedade comutativa refere-se a troca da ordem na operação, ou seja, que e são a mesma coisa. Vejamos através de um exemplo que a divisão não tem esta propriedade.
Se fizermos obtemos o resultado , agora se resolvemos , obteremos um resultado que nem é um número inteiro, porque estamos dividindo uma unidade inteira por duas partes iguais.
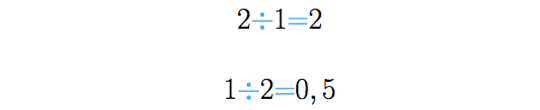
Podemos dizer, portanto, que dois dividido por um é diferente de um dividido por dois: , e que a divisão não tem a propriedade comutativa.
A propriedade associativa diz que quando temos uma expressão como podemos resolver de duas maneiras: associando os dois primeiros números, ou os dois últimos. Isto significa que o cálculo tem a propriedade associativa e a representamos assim Vamos ver se essa propriedade dá certo na divisão.
Resolvemos primeiro . Para começar resolvemos os parênteses e em seguida fazemos , para obter o resultado final.
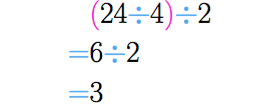
Por outro lado, resolvendo , começamos fazendo , que tem como resultado . Em seguida , e assim chegamos na resposta final.
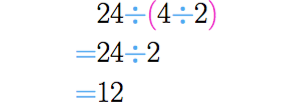
Como você pode ter percebido, os resultados finais foram diferentes, assim, podemos concluir que a divisão não tem a propriedade associativa.
/pt/divisao/propriedades-da-divisao-parte-ii/content/
