Temas básicos
Breve historia de los números I


/es/temas-basicos/proporcion-aurea/content/
En cerca del lugar donde nace el río Nilo, Jean Heinzelin de Braucourt descubrió un pequeño hueso que data de hace más de años. Además de ser tan antiguo, este huesecillo es el testimonio vivo de una de las hazañas intelectuales más grandes del hombre: el concepto de número. Es conocido como “hueso de Ishango”, nombre de la región africana donde fue hallado. En él están talladas una serie de muescas agrupadas de tal manera que revelan un entendimiento que va mucho más allá de contar.

Este fue el comienzo de los números, y de ser simples marcas en huesos de animales prehistóricos, han pasado a ser una de las herramientas más poderosas de la humanidad. ¿Pero cómo ha sido su desarrollo y que circunstancias lo propiciaron? En esta serie de artículos dedicados a la historia de los números, descubrirás esto y mucho más.
Existe una antigua tribu en Australia central, los Warlpiri, que prácticamente carece del concepto de número. Tienen dos palabras para representar cantidades: “solo” y “muchos”. Cuando se le pregunta a un anciano cuántos nietos tiene, sencillamente nombra a cada uno de ellos mientras traza líneas en la arena, y al final dice: “muchos”.
¿Cómo es posible que un pueblo con más de de años historia no haya desarrollado más conceptos numéricos? Por otra parte, los antiguos pueblos de oriente como los sumerios o los chinos desarrollaron no sólo números, sino métodos aritméticos que dejaron su huella hasta nuestros días.
Se atribuye esta diferencia en el desarrollo de los conceptos matemáticos a la creación de las grandes ciudades y centros urbanos. Pues en ellas se hace necesario organizar, almacenar y distribuir alimentos; además se debe tener una idea de la cantidad de habitantes y claro, recaudar impuestos.
Los babilonios por ejemplo, usaban un sistema de escritura llamado cuneiforme. Representaban las unidades con cuñas y así simbolizaban los números del al Para representar el diez usaban una cuña dispuesta horizontalmente. Para escribir los números del al les eran suficientes estos dos símbolos.

El era un número muy especial para ellos y era la base de su sistema. Usar este número trae sus ventajas pues es el número más pequeño divisible por , , , y , además también tiene como divisores a , , , y . Esto hace pensar que no fue escogido al azar sino gracias a sus propiedades, lo que a su vez deja ver que los babilonios tenían un gran dominio de la aritmética. Por supuesto, este poderoso pueblo dejó su marca hasta nuestros días: notarás que dividimos las horas del día en minutos y a su vez los minutos en segundos; pasa igual con la medida de los grados de la circunferencia, en total son que es , cada uno de estos grados se divide en minutos y cada minuto en segundos de arco, esto se lo debemos a los babilonios.
Los egipcios por su parte usaban representaciones un poco menos funcionales pero hicieron grandes aportes al desarrollo de los números. Empleaban un sistema en el que cada símbolo representaba diez veces lo que el anterior:
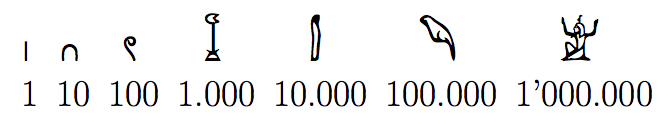
Para representar cantidades se ubicaban estos símbolos juntos y el valor de cada uno era sumado, conformando la cantidad total. Para representar el , por ejemplo, usaban los símbolos anteriores como se muestra en la siguiente imagen:
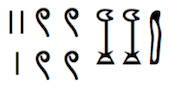
Uno de los aportes más grandes de los egipcios al desarrollo de los números fueron las fracciones, aunque sólo representaban las que tuvieran un uno como numerador, con excepción de y , que eran de un uso muy común. La concepción de este tipo de números es sin duda alguna un paso no solo necesario, sino que también profundo en el desarrollo de las matemáticas y la forma en la que esta nos ayuda a comprender el mundo.
Sin embargo, los desarrollos más impresionantes los hicieron los griegos. Estos le dieron un significado más amplio al concepto de número y a la matemática en general. Como sus antecesores, relacionaban los números con la divinidad y la perfección del universo. Tan es así, que uno de ellos casi enloquece al descubrir una nueva clase de números que contradecía toda su postura religiosa, hablamos nada menos que de Pitágoras. Veamos la historia.
/es/temas-basicos/breve-historia-de-los-numeros-ii/content/