Os números
Algumas propriedades do conjunto dos números racionais


/pt/os-numeros/o-que-sao-numeros-racionais-ou-fracionarios/content/
O conjunto dos números racionais tem características diferentes dos números naturais e dos inteiros, veja quais são elas:
Sabemos que os números racionais são expressões da forma onde e é diferente de zero. Veremos agora como os naturais e os inteiros também podem ser descritos desta forma.
Observe que é possível escrever cada número natural da forma que mencionamos anteriormente. Por exemplo, o um: Além portanto
Da mesma forma entendemos que todo número natural também é um número fracionário. Por exemplo, quinze unidades distribuidas em três partes iguais dá um total de cinco unidades. Isto quer dizer que já que
Assim é um subconjunto de , .
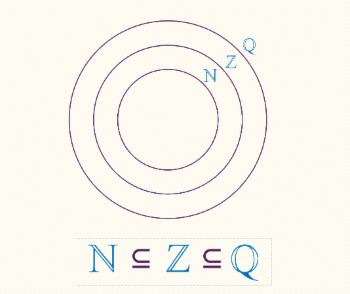
Uma vez tenhamos obtido os números naturais como frações, é fácil também obter os inteiros, por exemplo: , portanto . Podemos resumir as relações de continência entre os conjuntos numéricos como mostra a imagem acima.
Cada vez que definimos novos conjuntos ganhamos no número de operações que podemos realizar, isso também aconteceu com os conjuntos e .

Nos conjuntos dos números naturais podemos realizar operações de adição e multiplicação; no conjunto dos números inteiros , adição, multiplicação e subtração; mas no conjunto dos racionais ou fracionários , temos os símbolos necessários para também representar o resultado das divisões.
Cada vez que vamos somar, subtrair, multiplicar ou dividir números racionais, teremos como resultado um outro número racional.
Isto significa que finalmente temos um conjunto em que todas as operações básicas são bem definidas e aceitas.
Você acredita que se determinamos um número racional é possível encontrar seu sucessor? Vamos pensar em um número racional como o por exemplo. Qual é o próximo número racional depois do zero? Se estivéssemos restritos aos ou , o sucessor seria simplesmente o , no entanto, o conjunto de números racionais pode representar frações de unidades.
Isto significa que para encontrar o sucessor de zero devemos considerar a expressão do tipo que representa a parte da unidade mais próxima à zero.
Representamos as unidades com círculos. Se partimos uma unidade em duas partes iguais devemos representar cada uma delas com a expressão ;se partirmos em três, com a expressão , e assim por diante.
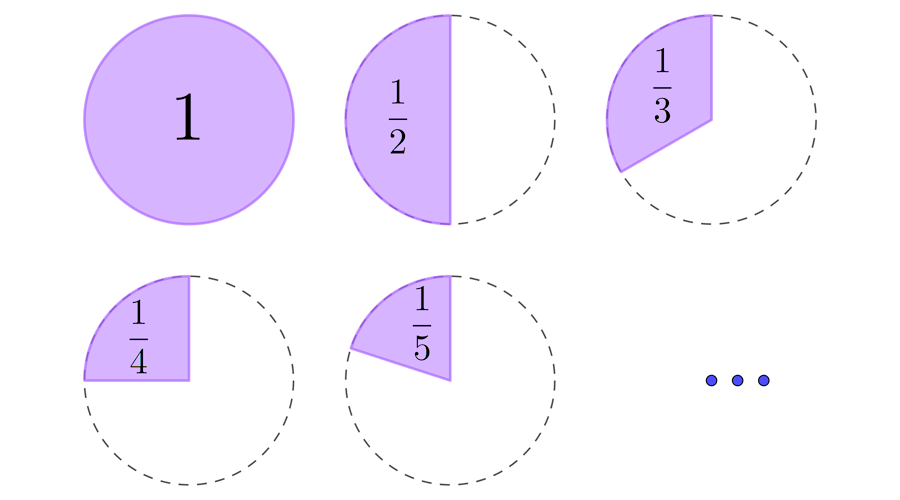
Na figura anterior, podemos ver as partes de unidades que representam as frações e ressaltado com cor. Como você pode ter percebido, quanto mais uma unidade é dividida, menor vai ficando cada parte. As expressões , , , etc. representam partes ainda menores.
Mas então ... quem é o sucessor de zero? Não existe! Os números fracionários não têm nenhum sucessor, ou seja, se pegarmos qualquer número racional não existe um que esteja na posição seguinte e que não tenha outros que estejam entre eles. Sempre que você escolher dois números racionais, por mais próximos que estejam, verá que entre eles existem infinitas frações.
/pt/os-numeros/ordem-no-conjunto-dos-numeros-racionais/content/