/pt/os-conjuntos-matematicos/operacoes-entre-conjuntos/content/
É possível usar os conceitos aprendidos aqui para interpretar e resolver alguns tipos de problemas, veja:
Vejamos a seguinte situação: numa sala de aula com crianças, gostam de sorvete de morango e de sorvete de chocolate. Se crianças não gostam de sorvete nem de morango nem de chocolate, quantas crianças gostam dos dois sabores? Quantas crianças no total gostam de sorvete de morango e quantas de chocolate?
A solução é mais fácil do que você imagina! Primeiro representamos a situação com o diagrama de Venn: chamaremos de o conjunto de alunos que gostam de sorvete de morango e o conjunto das crianças que gostam de sorvete de chocolate.
Estes dois conjuntos devem estar contidos num conjunto universal, que é precisamente a sala de aula completa com crianças. Portanto, podemos representar toda a situação através do seguinte esquema:
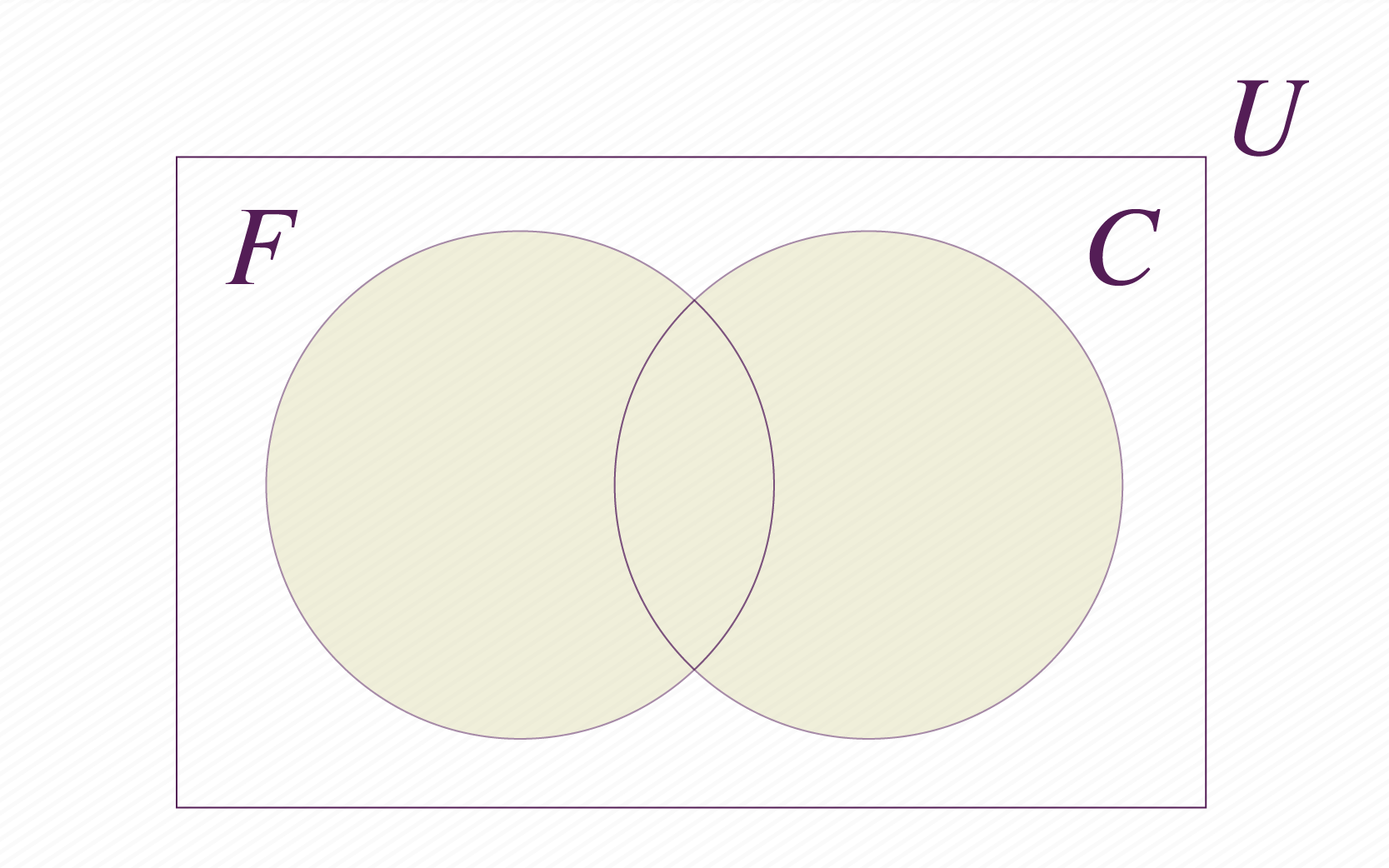
As diferentes partes do esquema acima representam os diferentes grupos de alunos. Por exemplo, na intersecção dos conjuntos e está representado as crianças que gostam dos dois sorvetes, enquanto que a parte que está fora em branco, representa a parte dos alunos que não gostam de nenhum sabor. Já podemos colocar os números dos estudantes nas áreas correspondentes:
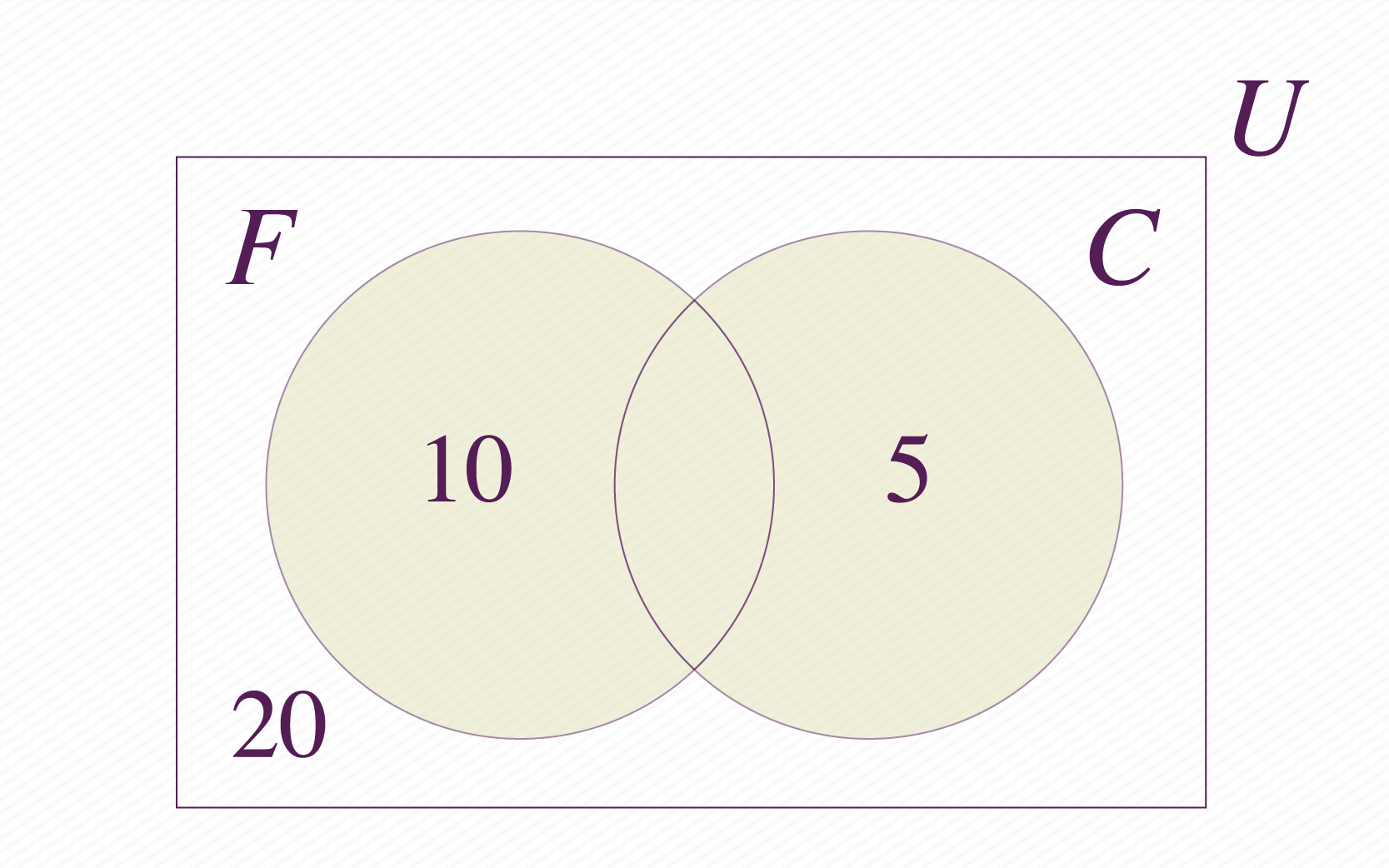
Note que o e o ficaram nas áreas dos estudantes que gostam de apenas um dos dois sorvetes, já o está localizado fora dos dois conjuntos, representando os estudantes que não gostam desses sabores de sorvete. Muito bem, temos estudantes que só gostam de sorvete de morango, só de chocolate e de nenhum dos dois, o que nos dá um total de .
Como a classe completa é de alunos, nos falta . Em qual grupo pertence esses alunos?
Há apenas uma opção: a área que gosta dos dois sorvetes, ou seja, a intersecção dos conjuntos e .
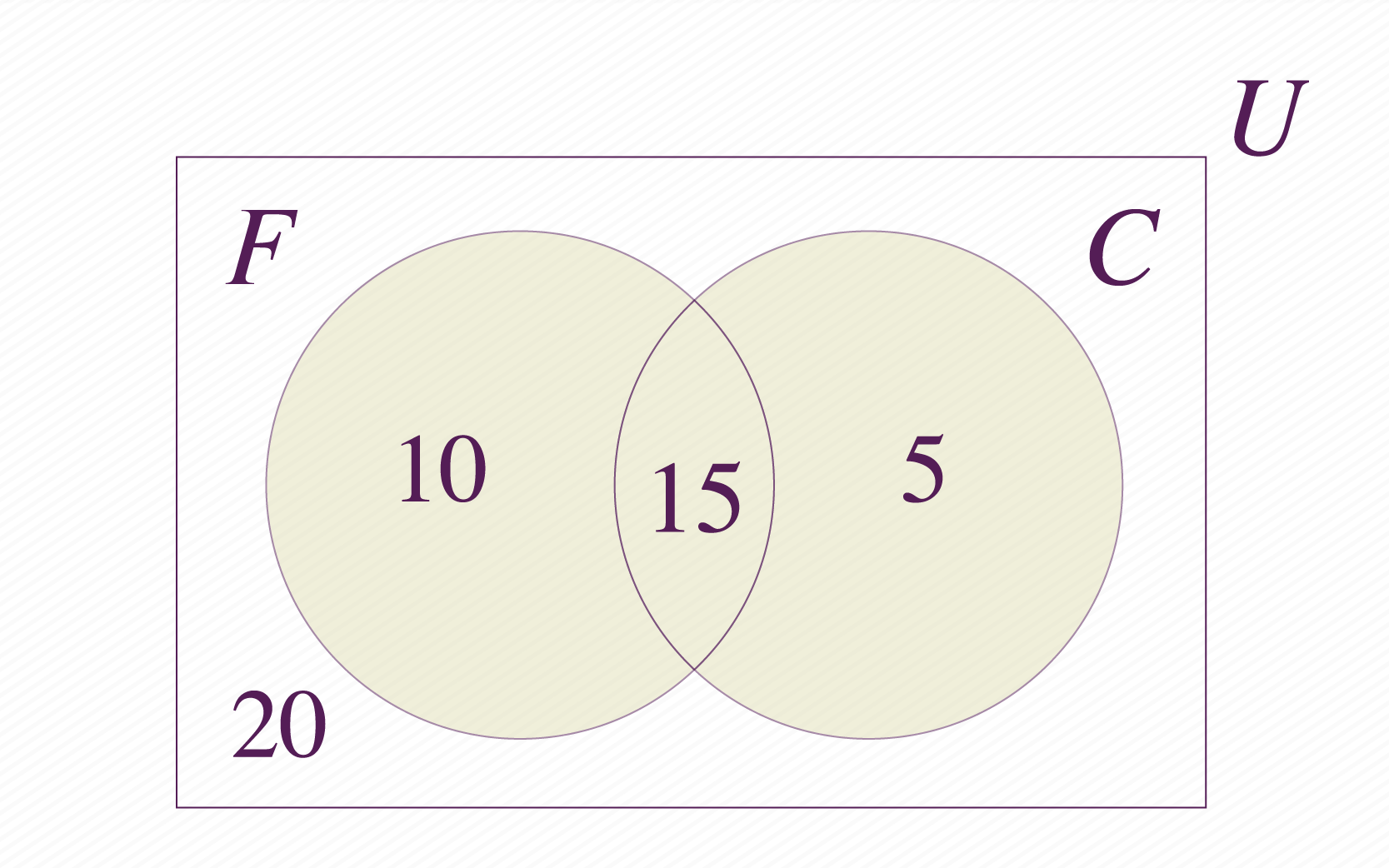
Podemos responder todas as perguntas feitas inicialmente: quinze estudantes gostam dos dois sorvetes. Há estudantes que gostam só de sorvete de morango e gostam dos dois sabores, no total, gostam de sorvete de morango. Há crianças que gostam apenas de sorvete de chocolate e que gostam dos dois, ou seja, estudantes gostam de sorvete de chocolate.
Uma última pergunta: Quantos estudantes gostam de sorvete de morango ou de chocolate?
Lembre-se que a união dos conjuntos é composta pelos elementos que pertencem a um ou a outro, portanto, a resposta é o número de crianças da união . Isto significa que crianças gostam de sorvete de morango ou de chocolate.
