/pt/numeros-fracionarios/alem-das-formulas/content/
Agora que você já sabe adicionar e subtrair todos os tipos de frações, pode usá-las para resolver problemas do seu dia a dia, observe:
Um fazendeiro semeia de sua fazenda com milho e com soja. Qual é a fração que representa o total semeado?
Aproveitemos o exercício anterior para fazer uma outra pergunta: qual fração da fazenda ainda não foi semeada?
Para responder devemos subtrair a totalidade da fazenda pela fração que foi semeada. Lembre-se de que o todo é representado pela unidade e desta forma, a totalidade da fazenda é representada pelo número . Devemos executar a subtração .
Para somar ou subtrair um número inteiro com uma fração, colocamos o um como denominador do número inteiro assim: . Lembre-se de que os inteiros e os naturais também possuem frações equivalentes.
Em seguida fazemos a adição ou a subtração de frações:
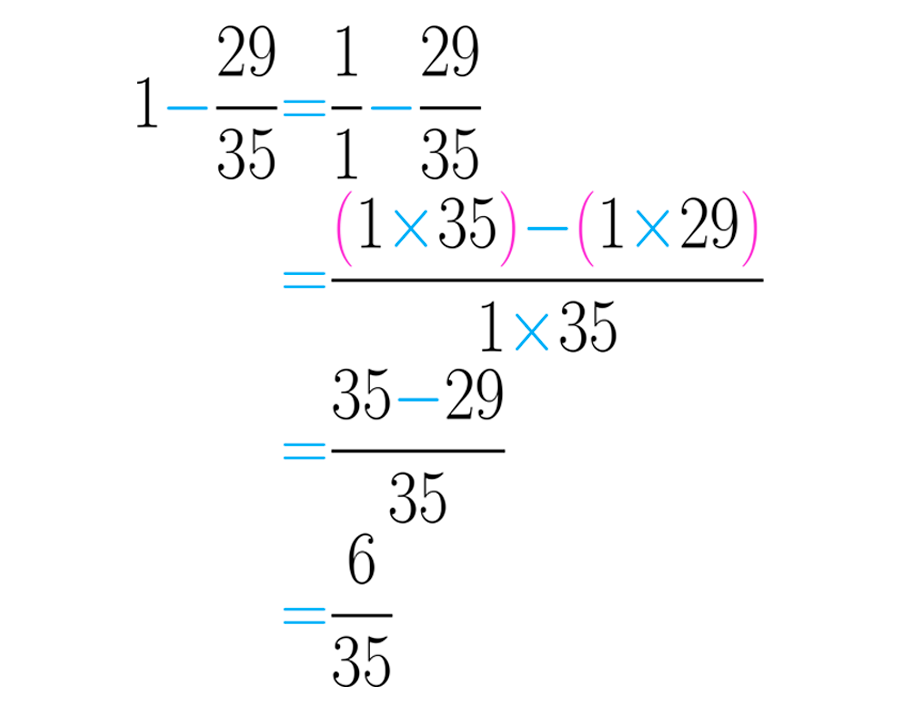
O resultado anterior significa que ficaram sem ser semeados da fazenda.
Um atleta decide treinar correndo numa determinada pista de corrida. No primeiro dia corre da pista, no segundo e no terceiro dia . Quantas voltas ele deu no total na pista?
Para determinar quantas voltas ele deu no total, devemos adicionar o que ele percorreu por dia. Aqui, em vez de usar a fórmula de soma, transformaremos as frações em equivalentes com denominador igual ao Mínimo Múltiplo Comum dos denominadores, :
Obtemos uma soma de frações homogêneas que é muito mais fácil de fazer. Agora, só precisamos somar os numeradores:
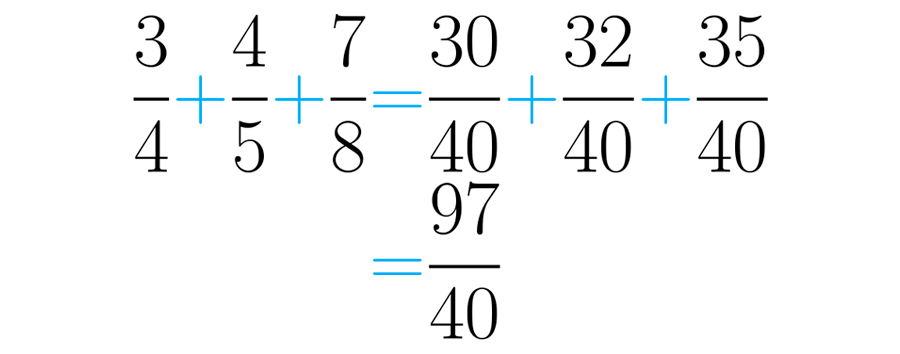
Para fazer isso fazemos a divisão . Lembre-se de que o quociente será a parte inteira do número, enquanto o resto será o numerador da parte fracionada:
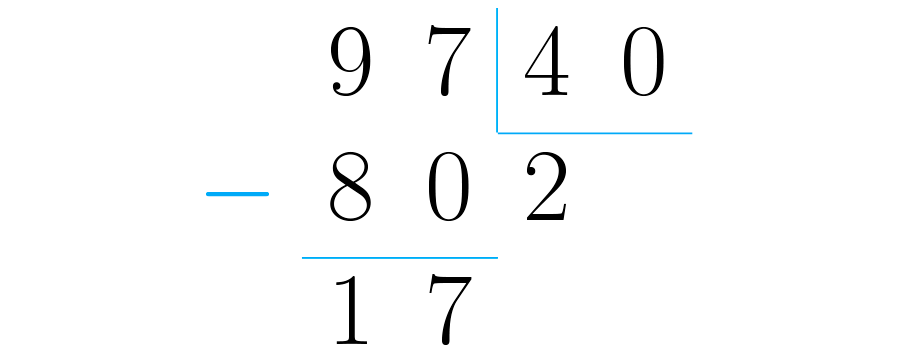
Graças a divisão anterior podemos dizer que é o mesmo que , ou seja, o atleta deu duas voltas e percorreu da pista a mais.
/pt/numeros-fracionarios/multiplicacao-de-fracoes/content/
