Los Conjuntos
Problemas de conjuntos


/es/los-conjuntos/operaciones-entre-conjuntos/content/
Es posible usar los conceptos aprendidos para interpretar y resolver cierto tipo de problemas, aprende cómo hacerlo.
Observa la siguiente situación: en un salón de clases de niños y niñas, a les gusta solo el helado de fresa y a solo el helado de chocolate. Si a niños no les gusta el helado ni de fresa ni de chocolate: ¿a cuántos niños les gustan los dos helados?, ¿a cuántos niños les gusta en total el helado de fresa?, ¿a cuántos el de chocolate?
¡Mira la solución, es más sencilla de lo que crees! Primero representaremos la situación con diagramas de Venn: llamaremos al conjunto de los estudiantes a los que les gusta el helado de fresa y al de conjunto de niños que gustan del helado de chocolate.
Estos dos conjuntos deben estar contenidos en un conjunto universal, que es precisamente el salón de clase completo. Por lo tanto podemos representar toda la situación a través del siguiente diagrama.
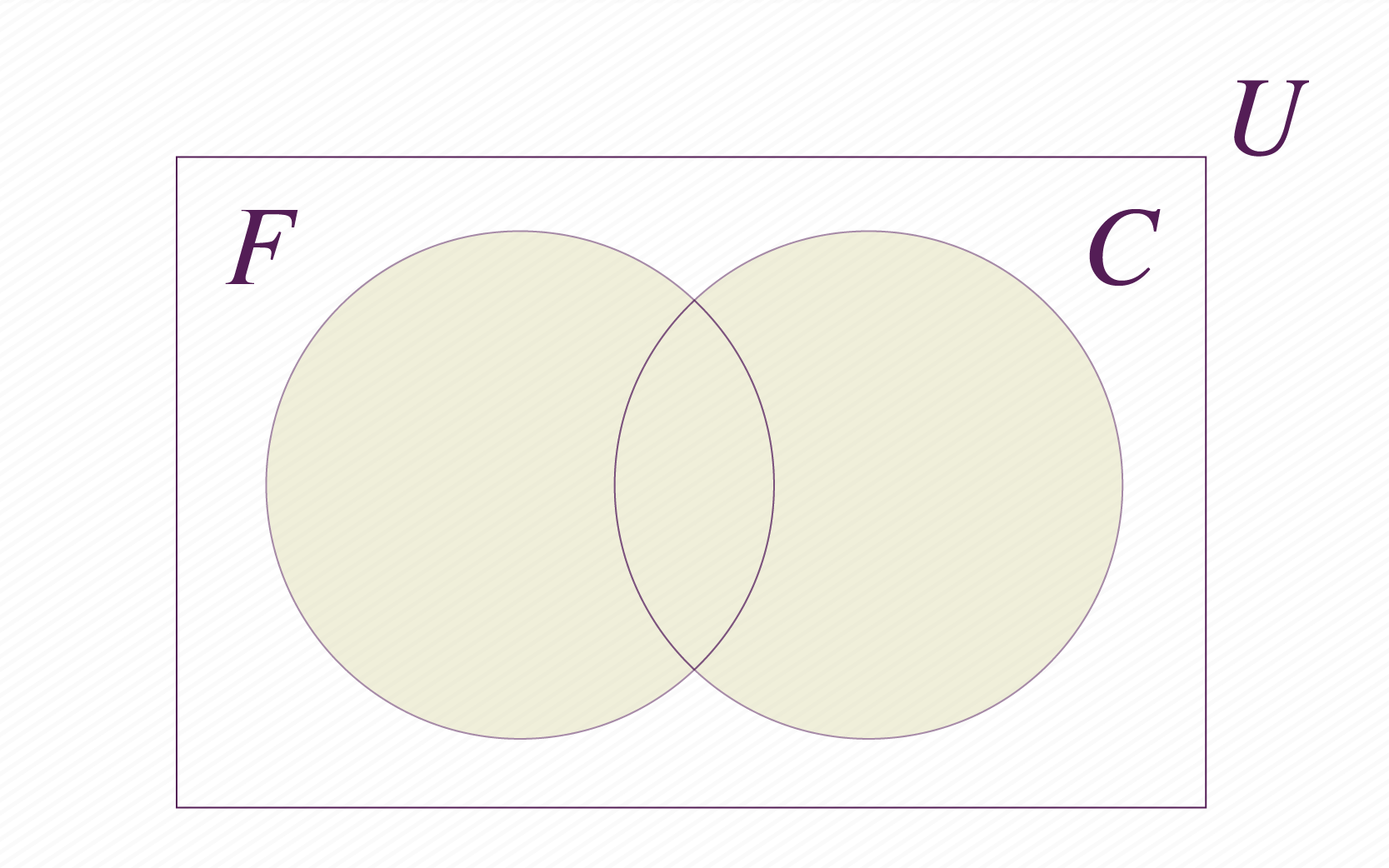
Las diferentes regiones del diagrama representan diferentes grupos de estudiantes. Por ejemplo, en la intersección de los conjuntos y , se representa la población de estudiantes que gustan de los dos helados, mientras que la región exterior a los conjuntos, representa la parte del curso que no gusta de ninguno. Podemos por lo tanto ubicar las cantidades de estudiantes en las zonas correspondientes:
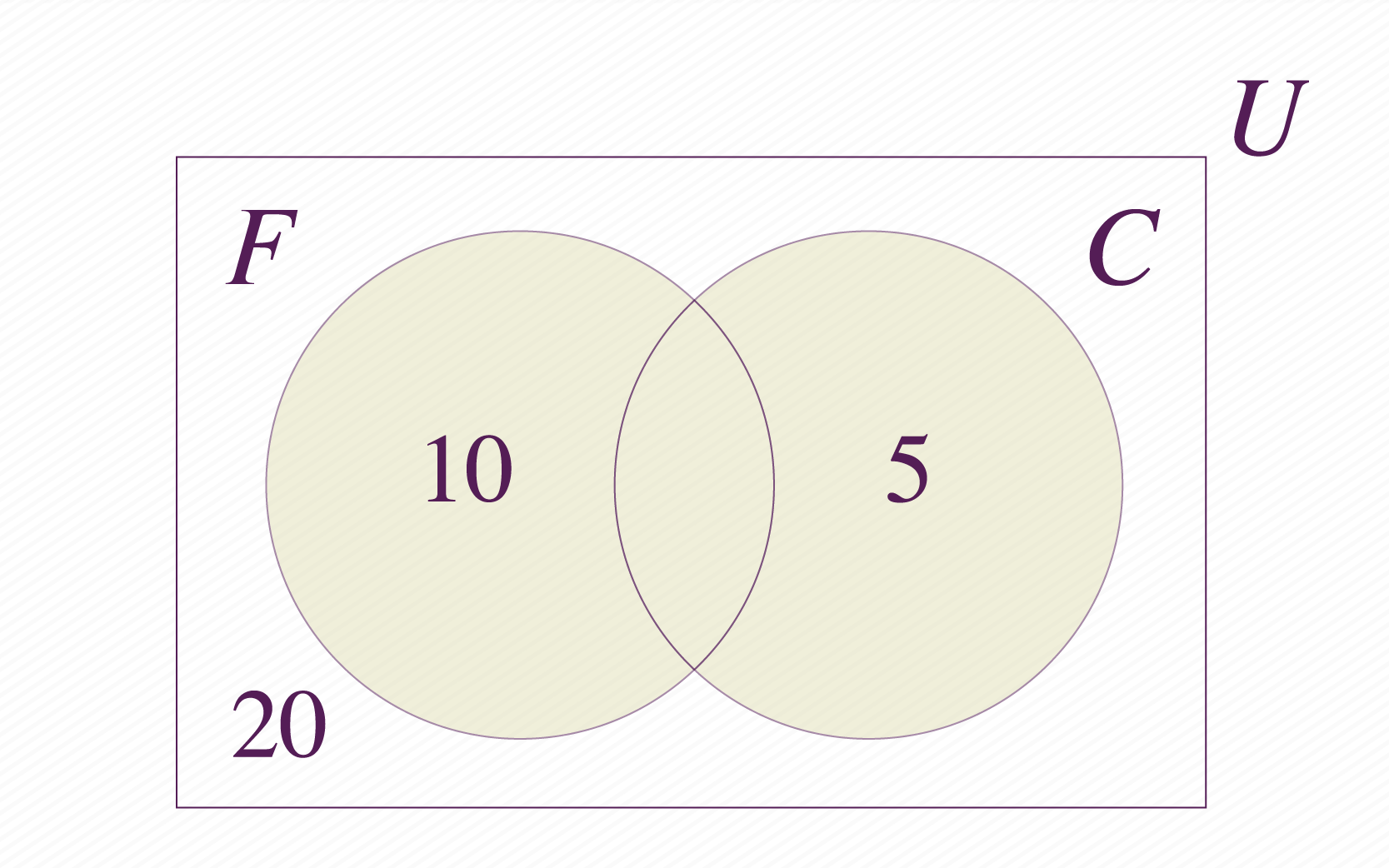
Observa que el y el quedaron ubicados en zonas que comprenden los estudiantes que gustan de solo de uno de los dos helados, por su parte el está ubicado por fuera de los dos conjuntos, representando los estudiantes que no gustan de estos sabores de helado, tal y como lo dice el enunciado del problema. Ahora bien, tenemos estudiantes que solo gustan del helado de fresa, solo el de chocolate y ninguno de los dos, lo que nos da un total de .
Como el curso completo se compone de estudiantes tenemos un faltante de . ¿A qué grupo pertenecen estos estudiantes?
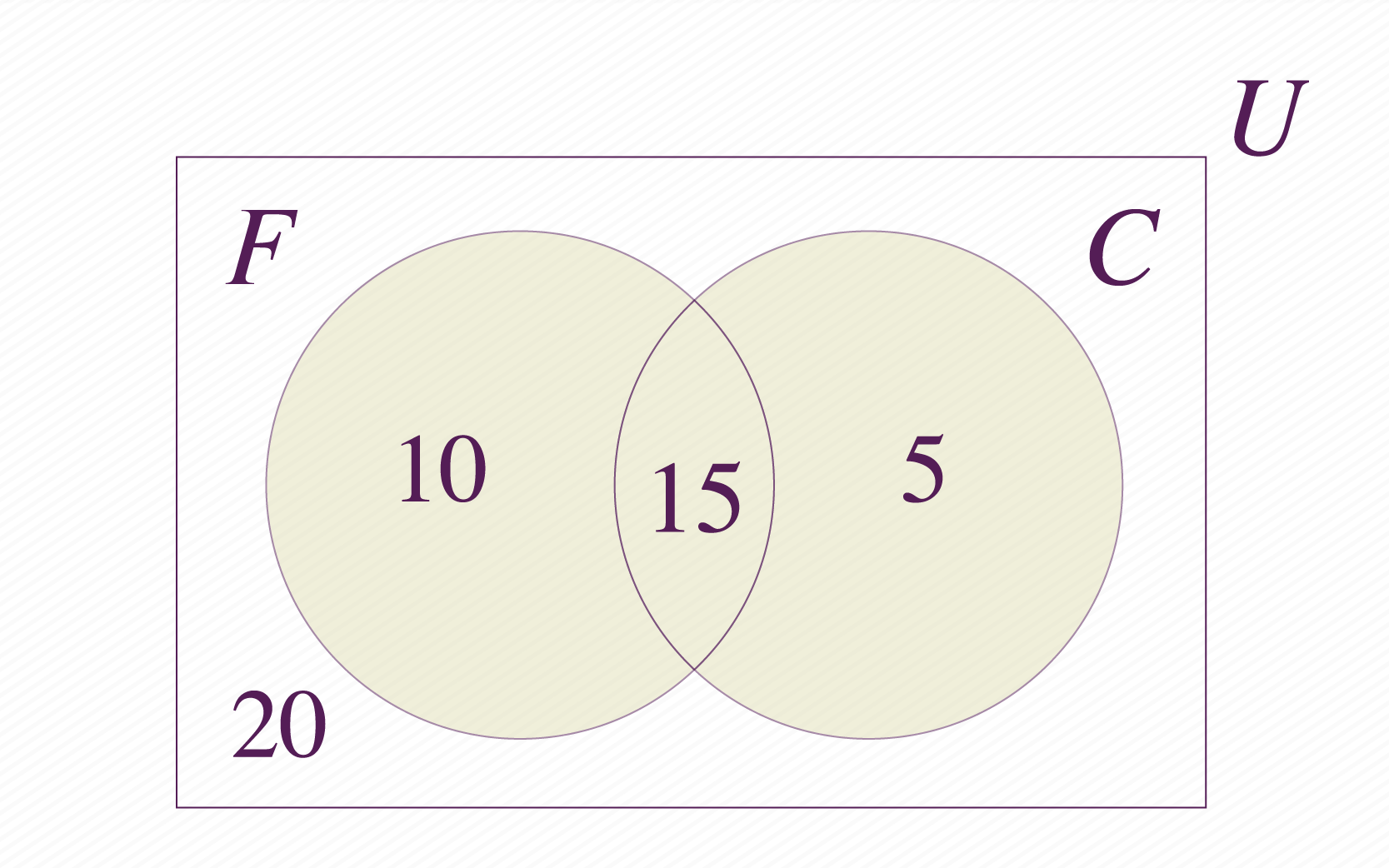
Podemos entonces responder todas las preguntas hechas inicialmente: a niños les gustan los dos helados, en total a les gusta el helado de fresa y a les gusta el helado de chocolate.
Una última pregunta: ¿a cuántos estudiantes les gusta el helado de fresa o el de chocolate?
Recuerda que la unión de conjuntos está conformada por los elementos que pertenecen a uno u otro, por lo tanto la respuesta es la cantidad de estudiantes de la unión . Esto quiere decir que a estudiantes les gusta el helado de fresa o el de chocolate.
/es/los-conjuntos/la-representacion-de-los-conjuntos/content/