/es/los-conjuntos/que-es-un-conjunto/content/

Notación de conjuntos

Como acabas de ver, es posible representar gráficamente los conjuntos a través de diagramas de Venn.  Para trabajar con ellos es necesario poder representarlos también con el lenguaje propio de la matemática.

Se usan los corchetes para representar y definir conjuntos.  En el interior de los corchetes se ubican los elementos que conforman el conjunto separados por comas.  Esta representación escrita es equivalente a la representación gráfica de diagramas de Venn.

Si por ejemplo se quiere definir el conjunto como el conformado por los elementos , , , y se puede representar de las siguientes formas:

Descripción de conjuntos por extensión

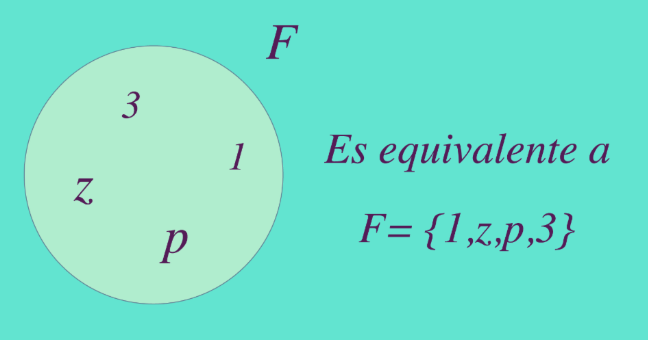
Para describir los elementos de un determinado conjunto los puedes mencionar uno a uno, a esto se conoce como descripción por extensión.  Definamos como el conjunto conformado por los colores del arco iris, en este caso podemos describir el conjunto por extensión así:

Si un conjunto tiene muchos elementos puedes hacer uso de los puntos suspensivos para describir el conjunto por extensión.  Por ejemplo, si el conjunto está conformado por los cien primeros números enteros, puedes representarlo de la siguiente manera:

En este caso no se muestran los cien elementos que conforman el conjunto.  Sin embargo, los puntos suspensivos representan todos los elementos que, por comodidad, no hemos escrito.

Descripción de conjuntos por comprensión

En algunos casos los conjuntos pueden tener una variada cantidad de elementos y la descripción por extensión resultaría muy ardua. Se puede entonces describir los conjuntos mencionando las características que comparten los elementos que los conforman.  Por ejemplo, si  es el conjunto conformado por todos los países del mundo se puede escribir:

En donde la barra | se lee como “tales que”.  Así, la anterior expresión se lee: “ es el conjunto de los  tales que  es un país”.  En este caso el símbolo es usado simplemente para representar los elementos del conjunto .

Conectivos

En algunas ocasiones los elementos que conforman un conjunto deben satisfacer más de una condición, o una de varias.  En tales casos se usan los conectivos disyunción y conjunción.

La disyunción

Para este caso, por ejemplo, la  abeja cumple la condición de volar, por lo que debe pertenecer al conjunto.  El gato por su parte cumple la condición de ser mamífero, por lo que también debe pertenecer a   El murciélago cumple las dos condiciones, ya que es un mamífero que vuela, así que también pertenece a

La conjunción

Definamos el conjunto  así: 

 

En este caso también hay dos condiciones pero están unidas por la conjunción “y”.  Esto significa que los elementos que pertenezcan al conjunto deben cumplir las dos condiciones simultáneamente.

Como no hay números que satisfagan las dos condiciones a la vez, se concluye que el conjunto  no tiene elementos.

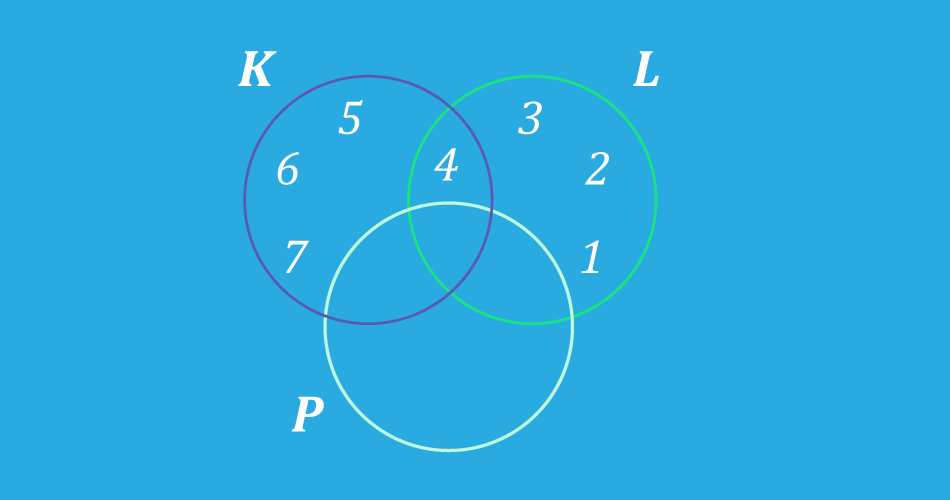
También es posible combinar los anteriores conectivos para establecer las condiciones que deben cumplir los elementos de un determinado conjunto.  Por ejemplo: sea 

Como te puedes dar cuenta, en la definición de los elementos del conjunto  hay dos condiciones: “ser mayor o igual que 4” y “ser menor que 8”, como estas condiciones están unidas por un “y” se deben cumplir ambas.  Entre tanto, la condición “ser mayor o igual que 4” esta compuesta por dos condiciones unidas por una disyunción, lo que significa que la cumplirán los números que sean mayores que  o iguales a . 

En el siguiente diagrama de Venn puedes ver la representación de los anteriores conjuntos y el conjunto 

Arrastra los elementos a sus conjuntos correspondientes:

/es/los-conjuntos/clases-de-conjuntos/content/