Divisores y múltiplos -

Propiedades de los divisores

Ir al curso

Divisores y múltiplos
Propiedades de los divisores

GCFGlobal Logo
search
person_outline arrow_drop_down
menu
navigate_before Curso

Divisores y múltiplos: Propiedades de los divisores

Página 7: Propiedades de los divisores

/es/divisores-y-multiplos/maximo-comun-divisor/content/

Propiedades de los divisores

Conocer las propiedades de los divisores te ayudará a familiarizarte con los mismos y a realizar las operaciones con más facilidad.

Todo número  distinto de cero es divisor del mismo

Siempre que calcules los divisores de un número natural dado, encontrarás que el número en cuestión está en la lista de los divisores.  Por ejemplo, los divisores de 20 son: Div(20)={1, 2, 4, 5, 10, 20} .  Fíjate que el mismo 20 hace parte de la lista de los divisores de 20 , esto sucede con todos los números.

La razón por la que esto ocurre es la siguiente: dado un número a , se tiene que a=1xxa .  Es decir, que a está una vez en a , o que el residuo de la división adiva es cero.  Recuerda que precisamente esas son las condiciones que definen el ser divisor.

Esta propiedad se puede representar de varias formas:

  • Para todo número a distinto de cero, a divide a a: a|a .
  • Para todo número a distinto de cero  a in Div(a) .

Uno es divisor de todo número

¿Has notado que cuando se calculan los divisores de un número, siempre aparece el uno?  Esto tiene una explicación: basta observar que para todo número a se cumple a=axx1 .  Por ejemplo, 5=5xx1 o 9=9xx1 .  Es decir, uno está a veces en a .  Por lo tanto 1|a .

Si un número es divisor de otros dos también lo es de su suma  y de su diferencia

Tomemos como ejemplo los números 3 , 15 y 9 .  3 es divisor de 15 y de 9 , según esta propiedad también debe ser divisor de su suma: 15+9=24 y de su resta: 15-9=6 .

Como puedes ver en la siguiente imagen, 3 hace parte del conjunto de divisores de 6 y de 24 .

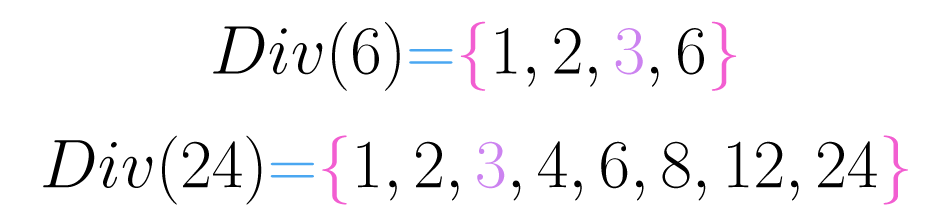
Divisores de 6 y 24.

Podemos generalizar esta propiedad así: dados tres números cualesquiera a , b y c si a|b y a|c , entonces a|(b+c) y también a|(b-c) .

Propiedad transitiva

Se puede enunciar esta propiedad así: si un número es divisor de otro y este lo es de un tercero, el primero es divisor del tercero.

Por ejemplo, 5 es divisor de 20 y a su vez 20 es divisor de 40 , la transitividad quiere decir que 5 debe ser divisor de 40 .

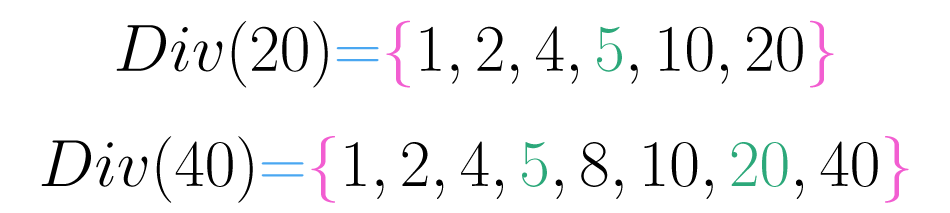
Divisores de 20 y 40.

Nota que cada divisor de 20 también es divisor de 40 .  Esta propiedad se generaliza así: dados tres números cualesquiera a , b y c si a|b y b|c entonces a|c .

Continuar

/es/divisores-y-multiplos/propiedades-del-maximo-comun-divisor/content/