Divisores y múltiplos
Máximo común divisor


/es/divisores-y-multiplos/la-descomposicion-prima-y-los-divisores/content/
El máximo común divisor es una de las herramientas más importantes en la aritmética, aprende a calcularlo.
Como has visto, los números pueden compartir varios de sus divisores. Por ejemplo, calculemos los divisores de y :
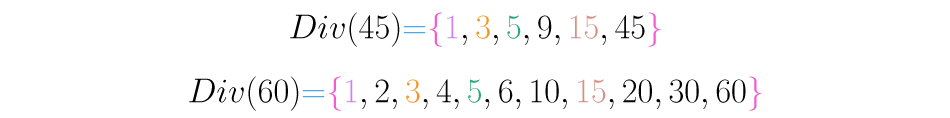
Observa que los números y son divisores comunes de y . Como verás más adelante, el mayor de estos números, el máximo común divisor, será muy útil en la realización de operaciones y en la simplificación de las mismas, es necesario entonces que lo aprendas a calcular.
Una forma obvia de calcular el máximo común divisor de varios números es exhibir todos los divisores de los números en cuestión, escoger uno a uno los comunes, y luego establecer cuál es el mayor de ellos. Para el caso de y , se tiene que el máximo común divisor es .
Sin embargo, este método no es lo más práctico siempre, ¿te imaginas calcular el máximo común divisor de números grandes como y ? ¡Para hacerlo tendríamos que encontrar cada uno de sus divisores y luego observar cuál es el mayor de ellos! Tal procedimiento no es el único, te explicaremos uno más sencillo y corto. veamos cómo calcular el máximo común divisor de y :
Primero se debe realizar la descomposición prima de cada uno de los números:

Se obtiene así que y .
Para calcular el máximo común divisor se multiplican los factores primos que sean comunes a los números, pero con el menor exponente con el que se encuentren.
En este caso los factores primos comunes son y . El menor exponente con el que aparecen estos factores es uno.
Debes tener en cuenta que cuando un número aparece sin exponente se considera que es uno. Por ejemplo,
Se debe multiplicar entonces , obteniendo que el máximo común divisor de y es .
Notamos el máximo común divisor de los números y así: . Podemos escribir entonces . Veamos otro ejemplo, calculemos el de , y .

Se puede afirmar que , y . Observa que y son los únicos factores primos comunes a estos tres números.
Ahora se multiplican los factores comunes con el menor exponente que aparezcan. El menor exponente con el que aparece el es uno, mientras que el menor exponente con el que parece el es dos, multiplicamos entonces .
De esta manera se encuentra que el máximo común divisor de , y es , es decir: .
Cuando el de dos números es uno, se dice que son primos relativos, coprimos o primos entre sí. Por ejemplo, si se descomponen los números y :
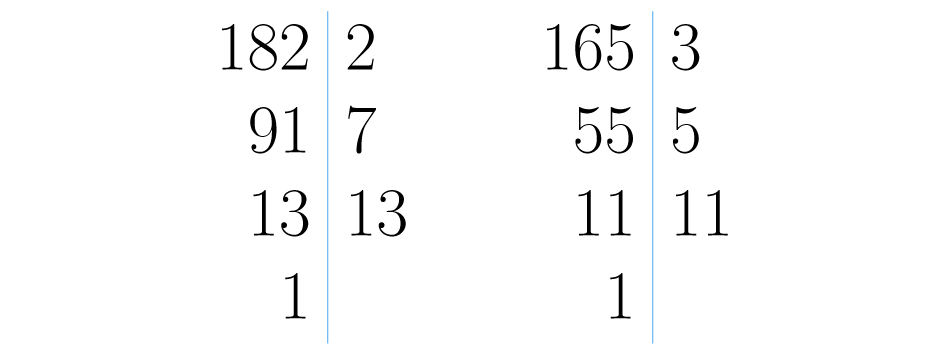
y . Que no haya factores primos en común, quiere decir que no tienen divisores comunes más que y por lo tanto:
Entonces y son primos relativos, coprimos o primos entre sí.
/es/divisores-y-multiplos/propiedades-de-los-divisores/content/