Divisores y múltiplos
Los números primos


/es/divisores-y-multiplos/que-son-los-divisores/content/
Los números primos juegan un papel fundamental en la matemática. Comprende este importante concepto:
Ahora que conoces el concepto de divisor podrás comprender qué es un número primo. Se dice que un número natural es primo si tiene solo dos divisores: uno, y él mismo.
Según lo anterior, dos es primo, pues ; tres es primo porque ; cinco es primo, por . Otros ejemplos de números primos son: etc.
A los números que no son primos los llamamos compuestos. Por ejemplo etc. son números compuestos. Al uno como excepción no se cataloga ni como primo ni como compuesto.
Como el conjunto de los números primos es tan importante, se usa un símbolo especial para representarlo, la letra .
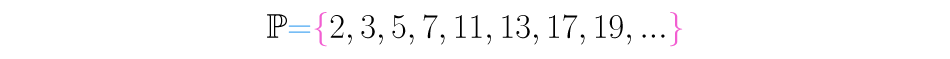
Observa que no hay un patrón para encontrarlos, no podrás hallarlos contando de dos en dos, o de tres en tres.
Desde la antigüedad los matemáticos se han interesado por este conjunto tan particular de números. Una de las primeras preguntas que surgió acerca de ellos fue cuántos existen. Euclides, matemático griego (325 - 265 a.C.), demostró que el conjunto es infinito. Es decir, no existe un número primo más grande que todos los demás, siempre que halles uno podrás encontrar otro mayor.
Hay varios procesos en los que es indispensable trabajar con números primos, así que debes estar en capacidad de encontrar algunos de ellos. El siguiente método para encontrar números primos es conocido como criba de Eratóstenes, su nombre se debe al ilustre matemático que la creo (276 - 194 a.C.).
Se comienza con una tabla en donde estén todos los números de un intervalo dado comenzando por el uno. La idea es eliminar uno a uno los números de tal forma que al final solo queden los primos. Por ejemplo, si queremos encontrar los primos del uno al cien podemos usar la siguiente tabla:
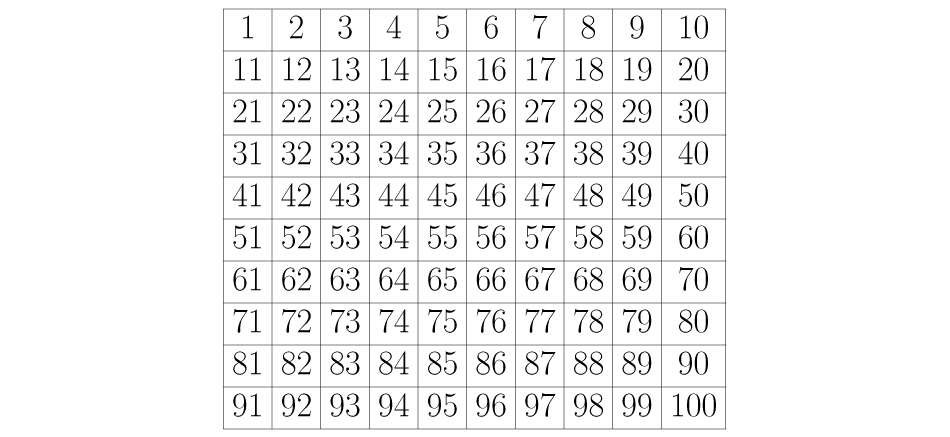
Se elimina el número de la lista ya que por definición no es un número primo.
Sigue con el número . Como no ha sido borrado, déjalo intacto. Sin embargo elimina todos los números que encuentres contando de dos en dos a partir de él.
Esto quiere decir que se deben borrar los números etc.
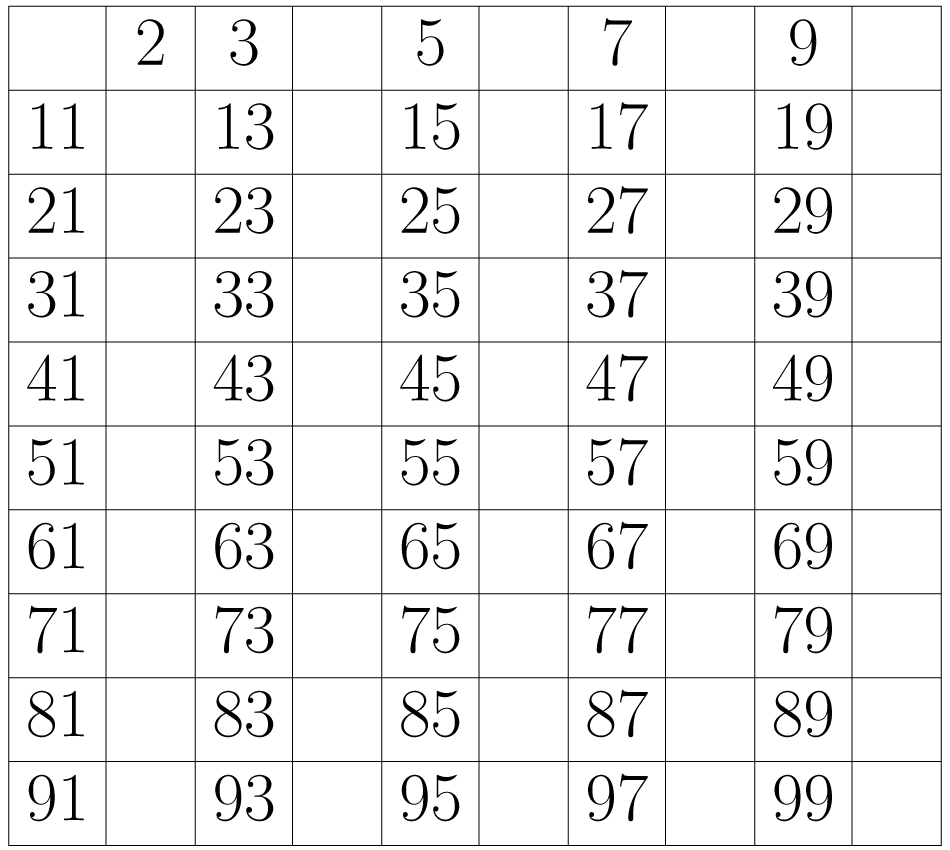
Continúa con el siguiente número que no haya sido eliminado, en este caso el tres.
Como no ha sido borrado déjalo en la tabla, pero a partir de él elimina todos los números que encuentres contando de tres en tres. Se deben borrar por lo tanto los números , , , etc.
La tabla se reduce a los siguientes números:
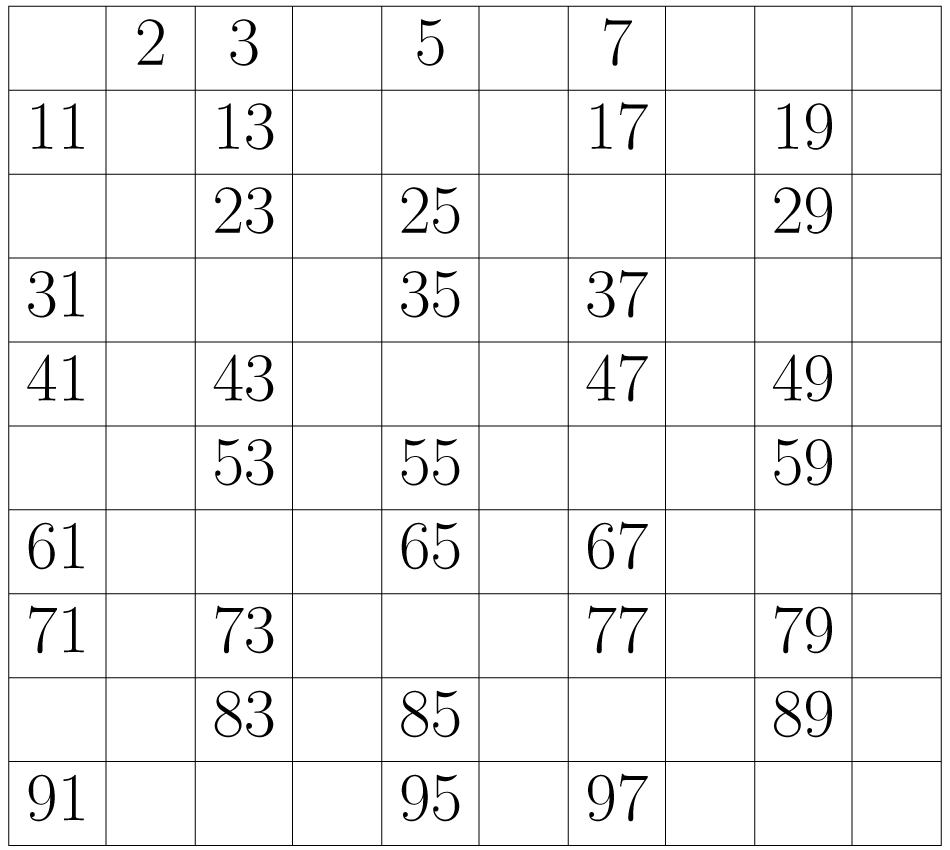
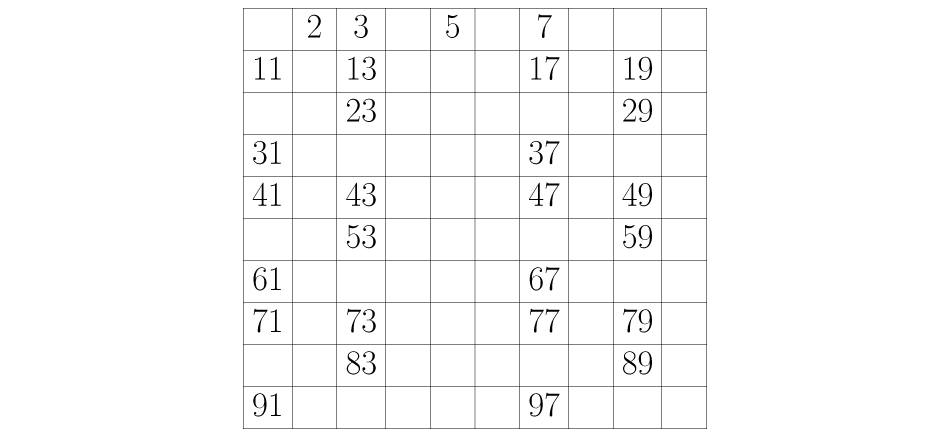
Se realiza el mismo proceso con todos los números que vayan quedando en la tabla: si un número no ha sido borrado se deja, pero se eliminan los que encontremos contando de tanto en tanto según sea el número en el que se esté. Siguiendo este procedimiento se encuentran todos los números primos entre uno y cien:
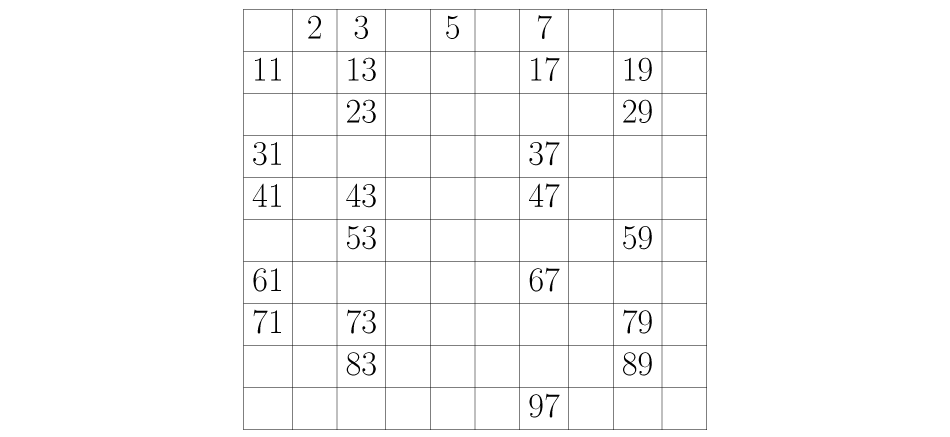
/es/divisores-y-multiplos/descomposicion-en-factores-primos/content/