Divisores y múltiplos
La descomposición prima y los divisores


/es/divisores-y-multiplos/descomposicion-en-numeros-primos/content/
La descomposición prima de un número tiene información sobre sus divisores. Aprende como interpretarla.
Una de las ventajas de encontrar la descomposición prima de un número es que nos permite saber cuántos divisores tiene y calcularlos fácilmente.
Observa: la descomposición prima de es . Si se usan las propiedades asociativa y conmutativa, se pueden encontrar descomposiciones no primas del número.
Por ejemplo, si se asocian los tres primeros factores y los tres últimos, se obtiene que . Esto permite concluir que y son divisores de :
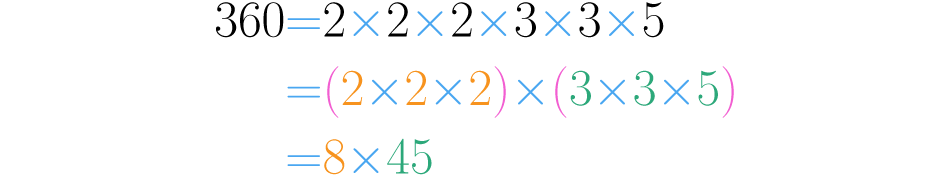
Si se conmuta y asocia de otra forma, se encuentran otros divisores: . De donde se tiene que y también son divisores de .
Todos los divisores de un número se producen al multiplicar las diferentes combinaciones de factores de su descomposición prima.
Al escribir la descomposición prima en forma de potencias es fácil determinar cuántos divisores tiene un número. Lo único que debes hacer es sumarle una unidad a cada exponente y multiplicar los resultados.
Siguiendo con el ejemplo de , si escribimos su descomposición en forma de potencias se tiene:
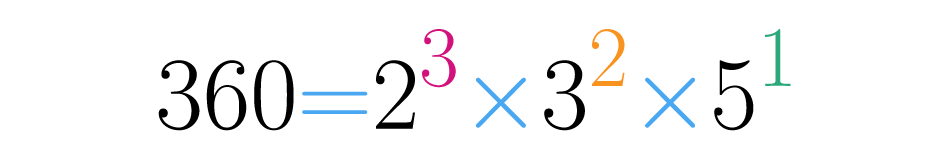
Los exponentes en esta descomposición son , y . Al sumarle una unidad a cada uno y multiplicar los resultados se obtiene:
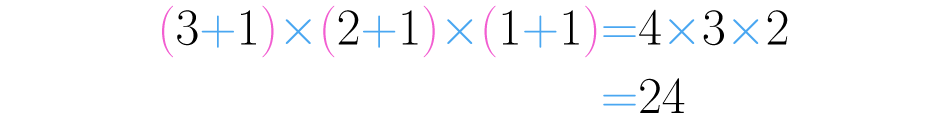
Esto quiere decir que tiene divisores.
Ya sabes que para obtener los divisores de un número se multiplican diferentes combinaciones de sus factores primos. Sin embargo, este proceso puede ser confuso, pues en algunas ocasiones es fácil olvidar algunas de estas combinaciones. Te brindamos un método para que los encuentres todos sin problemas. Sigamos con el número como ejemplo:
En este caso el primer factor primo es . Observa que su exponente es , entonces las distintas potencias son: y .
Se hace una fila con todos los resultados de esas potencias:

Se multiplica la fila del paso 1 por cada uno de estos números.
Como resultado obtenemos otras dos filas, para un total de tres.
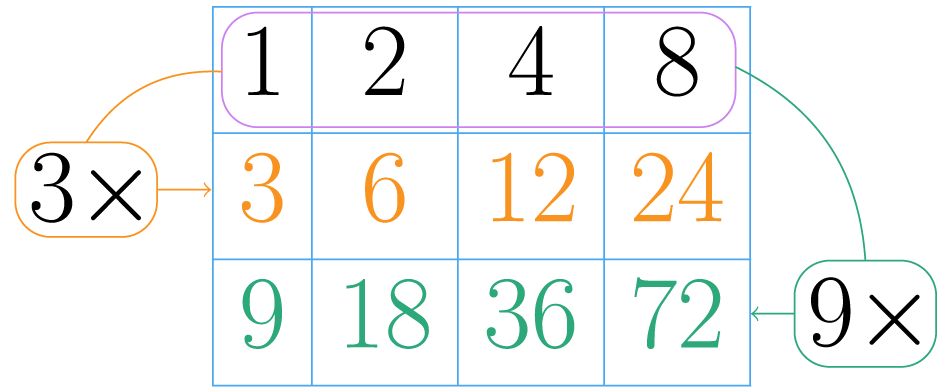
No es necesario tener en cuenta el factor pues al multiplicar la primera fila por se obtendría la misma fila sin alteraciones.
Ahora se debe repetir el paso anterior con todas las potencias del tercer factor. En este caso el tercer factor es y como tiene exponente , solo multiplicamos las filas anteriores por .
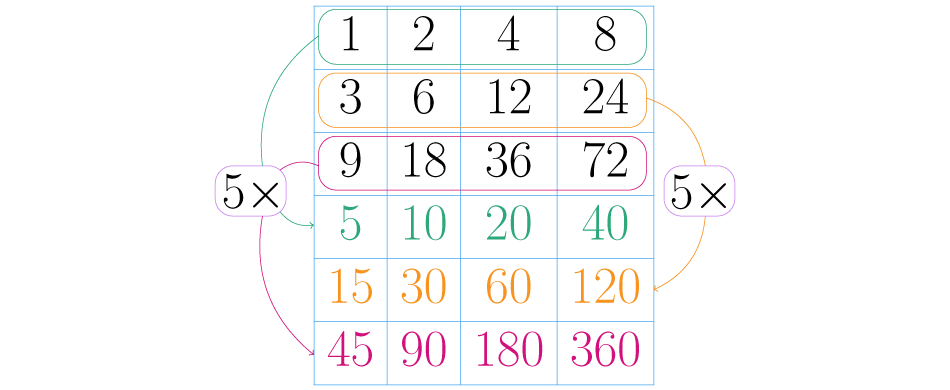
Si el exponente del hubiera sido por ejemplo , se tendría que multiplicar cada fila también por , lo que produciría tres filas adicionales.
Como no hay más factores en la descomposición de se ha terminado el proceso. Observa que en la tabla hay exactamente números, estos son todos los divisores del .
/es/divisores-y-multiplos/maximo-comun-divisor/content/