Aplicaciones de la matemática
La corona del rey y la bañera de Arquímedes


/es/aplicaciones-de-la-matematica/las-coordenadas-geograficas/content/
Tal vez, en alguna ocasión, pensaste en comprar alguna joya de oro para un obsequio o para ti mismo. Pendientes, cadenillas, anillos o gargantillas son algunos de los objetos más codiciados por algunas personas. Si no eres un experto en joyas es probable que dudes si dicho objeto es de oro o te estén timando. No sería extraño dar con algún comerciante de pocos escrúpulos que quiera pasarse de listo con personas que no conocen del tema.
Cuenta la historia que hace mucho tiempo, un rey mandó a elaborar un corona de oro y tuvo la misma incertidumbre, pero gracias a la pericia de un eminente pensador logró saber si era engañado o no. Quizás, cuando conozcas el método usado para descifrar si había truco, no seas una presa tan fácil para los timadores.
El rey Hierón II (306 - 215 a.C.), de Siracusa, destinó cierta cantidad de oro para la fabricación de una corona. El material se envió a un reconocido orfebre a quien se le pidió fabricarla sin usar otro material, ni siquiera piedras preciosas como diamantes o rubíes. Tiempo después el artesano devolvió al rey una fantástica pieza, una preciosa corona digna de los mejores elogios. La corona gustó al rey, sin embargo este desconfiaba de que estuviera hecha con todo el oro destinado para ella. Tal vez el artesano había mezclado el oro con otros materiales para quedarse con el parte del preciado metal.
En aquella época vivía en Siracusa uno de los hombres más inteligentes de la historia de la humanidad: Arquímedes. A este personaje se le designó la difícil tarea de demostrar que la corona era de oro puro, o si por el contrario el orfebre trataba de engañar al rey. Claro, Arquímedes debía encontrar la solución sin causar daño alguno a la costosa joya.
Para entender cuál fue la solución que encontró Arquímedes primero debemos comprender algunos conceptos veamos:
Mientras que la masa y el volumen son características físicas propias de un cuerpo en particular, la densidad es una medida que relaciona estas dos. Para calcularla debemos dividir la masa del cuerpo entre su volumen. Por ejemplo, si un cuerpo tiene una masa de kilogramos y un volumen de metros cúbicos, su densidad será de kilos por cada metro cúbico :
Este concepto nos da una idea acerca de la concentración de materia que tiene un cuerpo por unidad de volumen. Lo interesante de esto es que cada elemento tiene su densidad específica. Es decir, no importa de que cantidad de masa estemos hablando, bajo ciertas condiciones, si se trata del mismo material, siempre que se divida su masa entre su volumen, nos dará el mismo número.
Veamos por ejemplo cuál sería la densidad del agua en condiciones de temperatura normales: centímetros cúbicos pesan gramos, mientras que centímetros cúbicos pesan gramos. Si calculamos la densidades tenemos:
y
Esto es: la densidad del agua a temperatura ambiente es de . Como ves la densidad no cambió. Esto mismo pasa con los diferentes materiales, como por ejemplo el oro.
Continuando con la historia, cierto día Arquímedes, que pasó mucho tiempo sin resolver el problema, decidió tomar un baño. Cuando hundió su cuerpo en el agua se dió cuenta que el agua se desplazaba, incluso parte de ella se rebosó saliendo de la tina en la que se encontraba. Al darse cuenta de esto, Arquímedes pensó que el volumen de agua que se desplaza es igual al volumen del cuerpo que se sumerge en ella. ¡Hay estaba la solución, en el agua! Se dice que fue tanta su emoción que inmediatamente salió desnudo corriendo por las calles y gritando a los cuatro vientos ¡Eureka!, ¡eureka!, que quiere decir ¡La he encontrado!
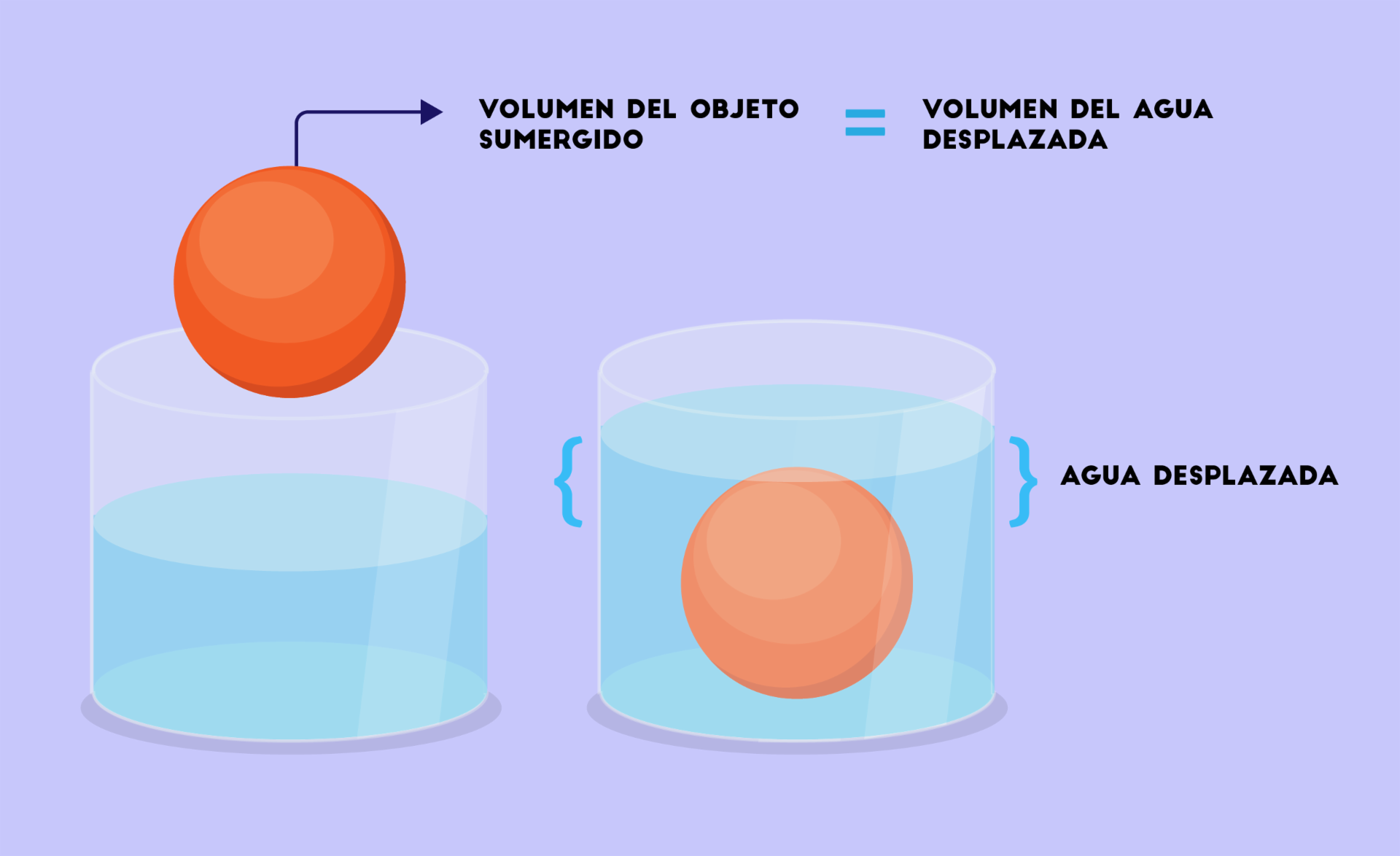
Gracias al descubrimiento de Arquímedes, el problema de la corona era ahora fácil de resolver ya que había encontrado la forma de medir el volumen de esta. Solo bastaba sumergirla y medir el volumen de agua que se desplazaba, este debía ser igual al volumen de la corona. Conociendo su masa y su volumen podría calcular su densidad y de esta manera verificar si se trataba o no de oro puro. Este hallazgo dio paso a un nuevo concepto físico.
Nuestro perspicaz amigo también descubrió que el agua desplazada hace una fuerza hacia arriba a los objetos que se sumergen en ella, por esta razón cuando levantamos algo bajo el agua es mucho más liviano. Esta fuerza depende directamente del volumen de agua que se desplaza: a más volumen de agua se desplace, más fuerza de empuje hacia arriba sufre el cuerpo sumergido. Este fenómeno físico es conocido como el principio de Arquímedes.

Es posible usar el principio de Arquímedes para saber si la corona estaba o no hecha completamente de oro:
En uno de los platillos de una balanza, se pone una cantidad de oro que pese exactamente lo mismo que la entregada por el rey al artesano, en el otro platillo de la balanza debe ser puesta la corona. Ahora piensa en esto: el oro entregado por el rey para la elaboración de la corona ocupa un determinado volumen, y este no cambiará al darle la forma de corona, si la corona no tiene alteraciones debe tener el mismo volumen que el oro dispuesto para su elaboración. Por el contrario si corona está alterada con otro material como por ejemplo cobre, su volumen será mayor, ya que para conservar el peso original debe usarse una cantidad de cobre que iguale el peso del oro hurtado, y como el cobre es menos denso que el oro se deberá usar un mayor volumen del mismo.
Así pues, en el aire, la corona y el oro pesan lo mismo; pero si se sumergen en el agua, la corona alterada sufrirá más fuerza de empuje hacia arriba debido a que su volumen será mayor y desplazará más agua. Por lo tanto la balanza se inclinará como se muestra en la animación de abajo:

Como ves, Arquímedes era un hombre mucho más que brillante, a su ingenio le debemos innumerables contribuciones a la matemática, el tornillo sin fin, la palanca y muchos otros. Sobre esta última Arquímedes pronunció: “dadme un punto de apoyo y moveré el mundo”.
Lamentablemente Arquímedes fue asesinado por un soldado cuando el ejército romano, comandado por el General Marcelo, saqueaba Siracusa. Marcelo dio la orden estricta de no hacer daño a tan ilustre personaje. Cuando un soldado romano lo encontró concentrado en un problema geométrico, trato de llevarlo a presencia del General. Sin embargo Arquímedes no le prestó atención y el soldado lo atravesó con su espada. Las últimas palabras de Arquímedes fueron: “No toques mis círculos”.
/es/aplicaciones-de-la-matematica/el-porque-de-las-estaciones/content/