Statistics: Basic Concepts: Line Graphs

Lesson 7: Line Graphs

/en/statistics-basic-concepts/pie-charts/content/

Line graphs

What is a line graph?

So far we’ve talked about bar charts, which are made up of bars, and pie charts, which are made up of slices or sections to represent data. There is also another type of graph called a line graph, which is made up of a series of points.

These points can be joined to form a complete line, showing how one variable changes over time. The points are “plotted” on a graph which has an x-axis and a y-axis, not unlike a bar chart.

The x-axis and y-axis represent different variables. Oftentimes the “independent variable” goes on the x-axis, and the “dependent variable” goes on the y-axis.

An independent variable is often something constant, like time, and the dependent variable is the variable that keeps changing, in relation to the other variable.

Quick Example: Maybe you want to measure how many centimeters your plant grows each month. Time is the independent variable, so months would go on the x-axis. Since the plant keeps getting taller, its height in centimeters would go on the y-axis.

Making a line graph

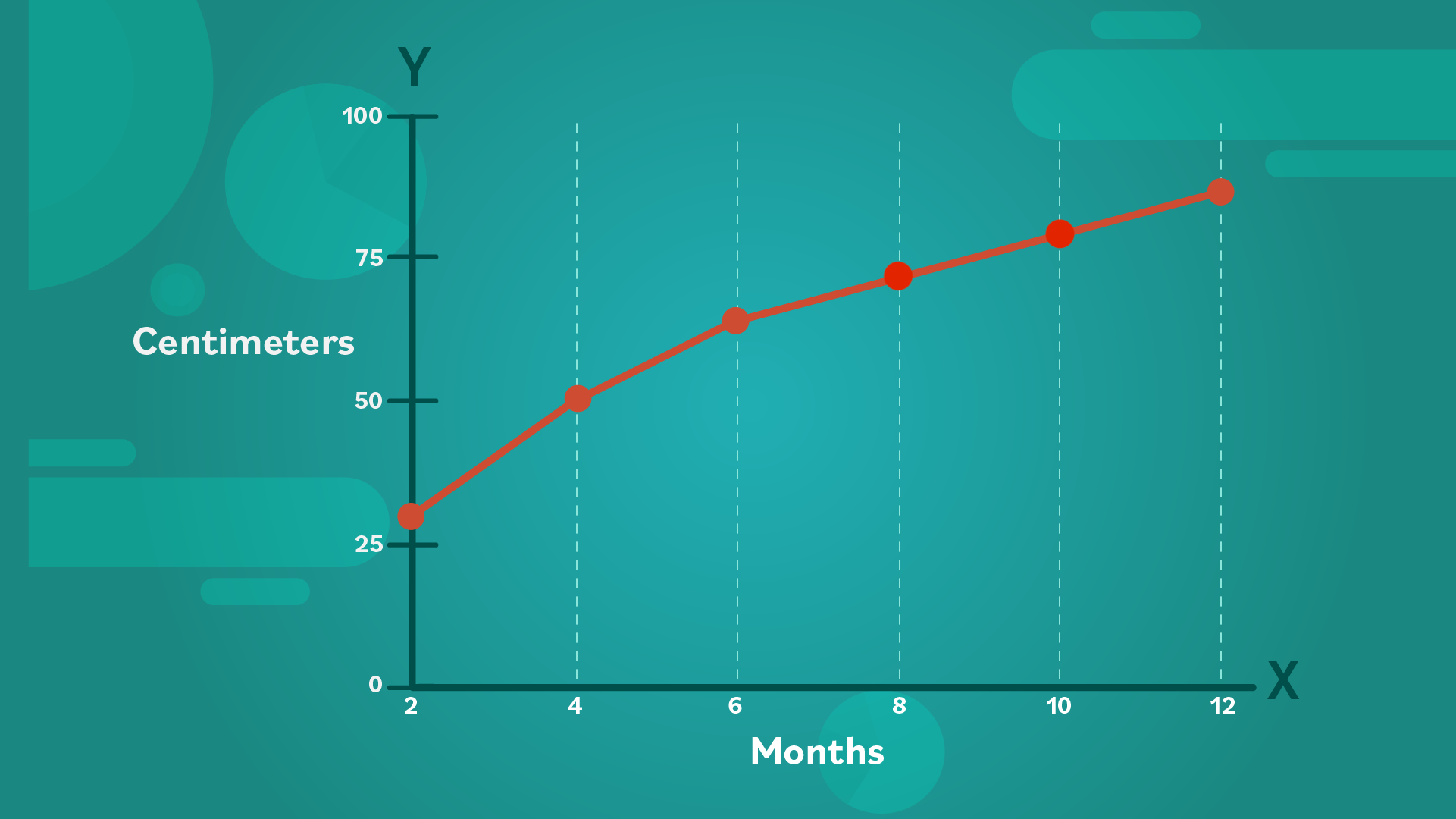
Let’s use another example to make a line graph…

City planners want to see how much a small city has grown in the last five years. This is their data set:

In the first year, 10 buildings were built. After two years, there were a total of 20 buildings. In three years: 35 buildings, four years: 50 buildings, and five years: 100 buildings in total.

Step 1: The first step is to organize the data into a table. There is one column for the years, and one column for the number of buildings.

Step 2: Next, the city planners start drawing their graph. Let’s put time as the variable on the x-axis, with an interval of 1. We should be able to include all five years.
Step 3: The number of buildings will be on the y-axis. Since the y-axis starts at 0 and the largest value is 100, 25 might be a good interval (0, 25, 50, 75, and 100).
Step 4: The planners use their table to plot each point on the graph. Look at the values on the x-axis, first (from Column 1), and then the corresponding value on the y-axis (from Column 2). Where these two values intersect determines the location of each data point.

Step 5: Now the planners can connect each point in order to make the line graph. We can see how the number of buildings has gone up quite a bit in the last five years.

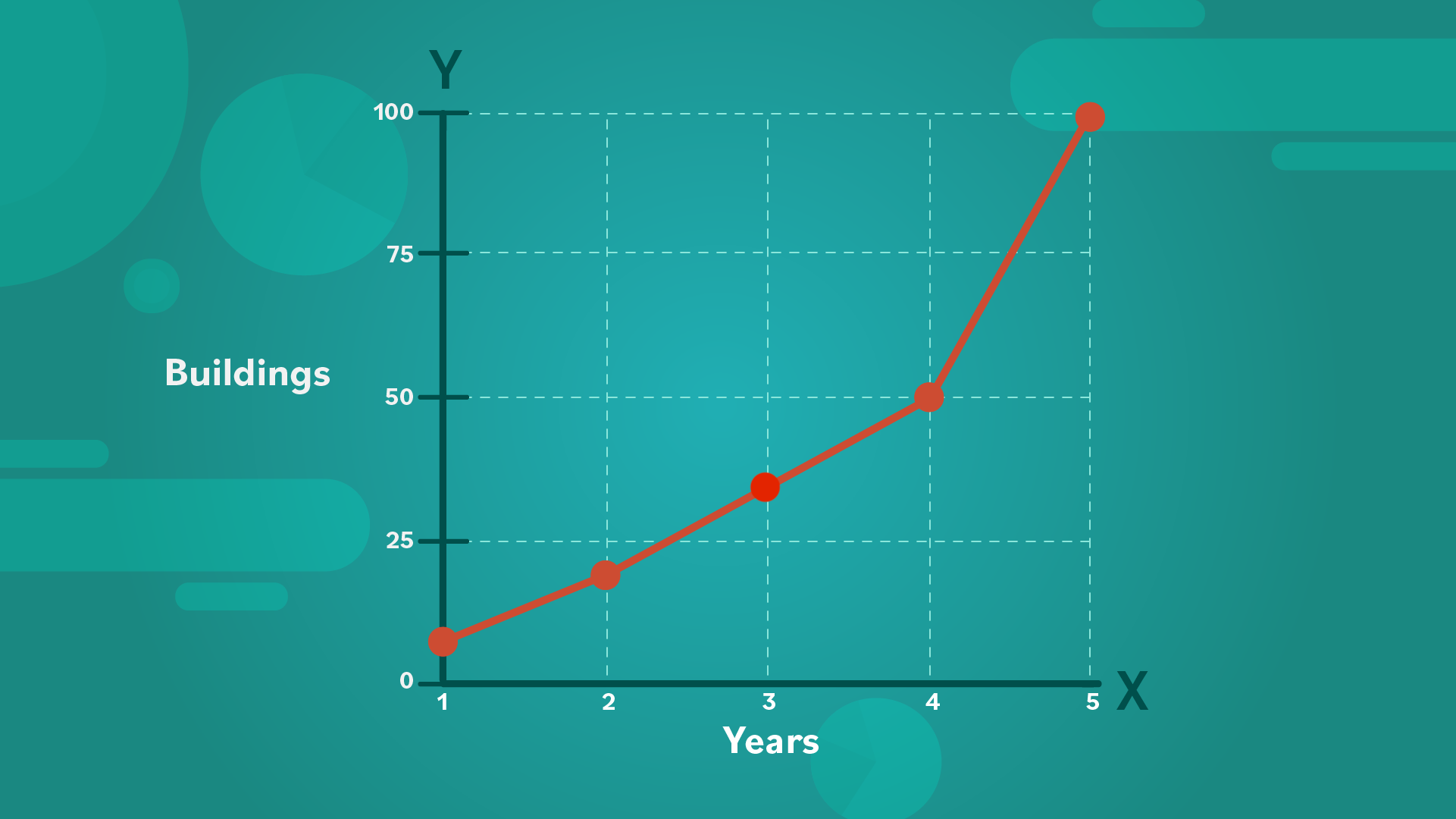
Next up, we’ll learn about another type of graph called a histogram.