Statistics: Basic Concepts -
Frequency Polygons

Statistics: Basic Concepts
Frequency Polygons


/en/statistics-basic-concepts/histograms/content/
A frequency polygon shows the overall distribution of a data set. It looks a little bit like a line graph–but the points on the graph can be plotted using data from a histogram or a frequency table.
Frequency polygons are especially useful for comparing two data sets. In our example, we’ll use the histogram from the last lesson in order to make our frequency polygon.
How to create a frequency polygon
Here is our histogram from the previous lesson, which shows the age range of members of the orchestra:
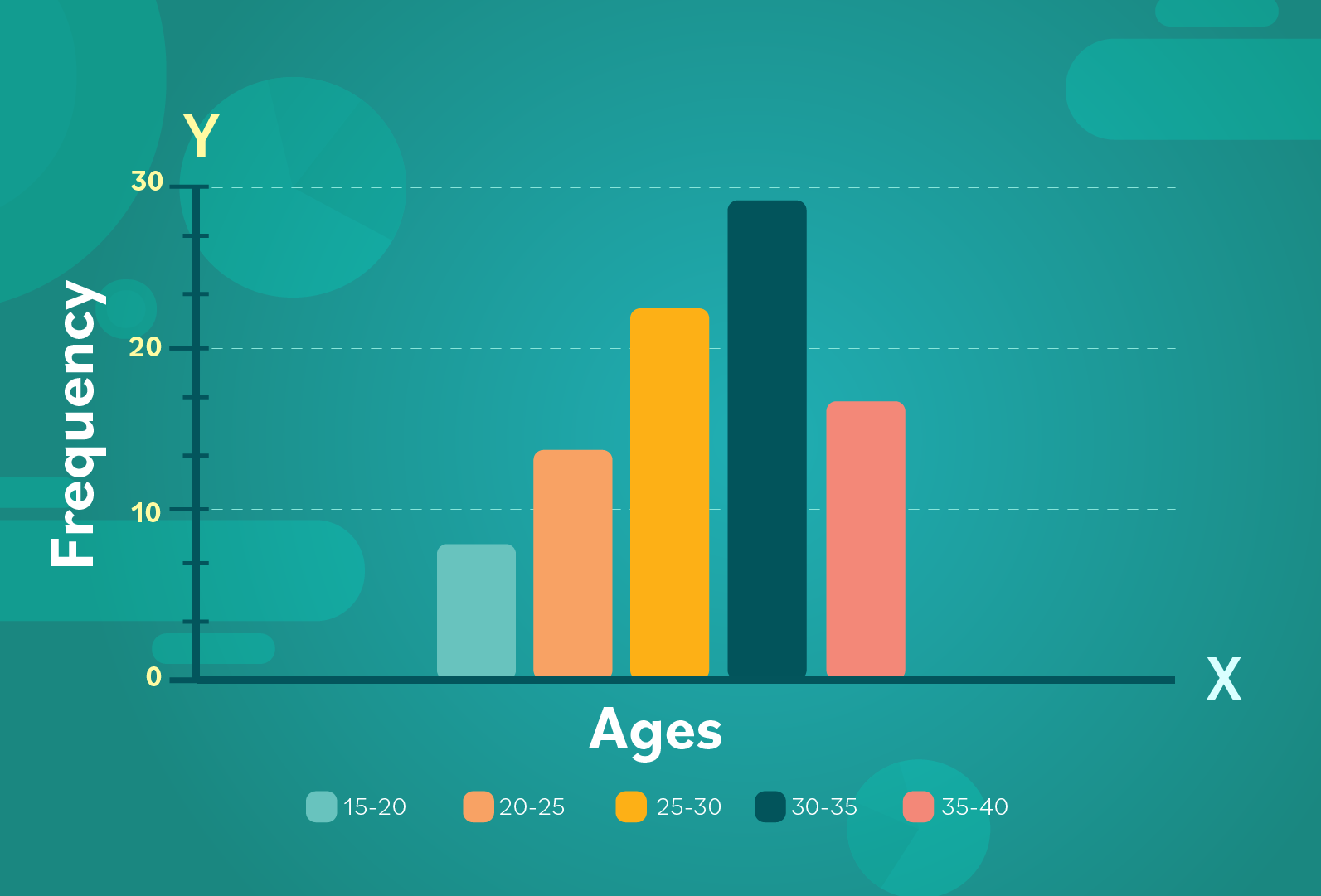
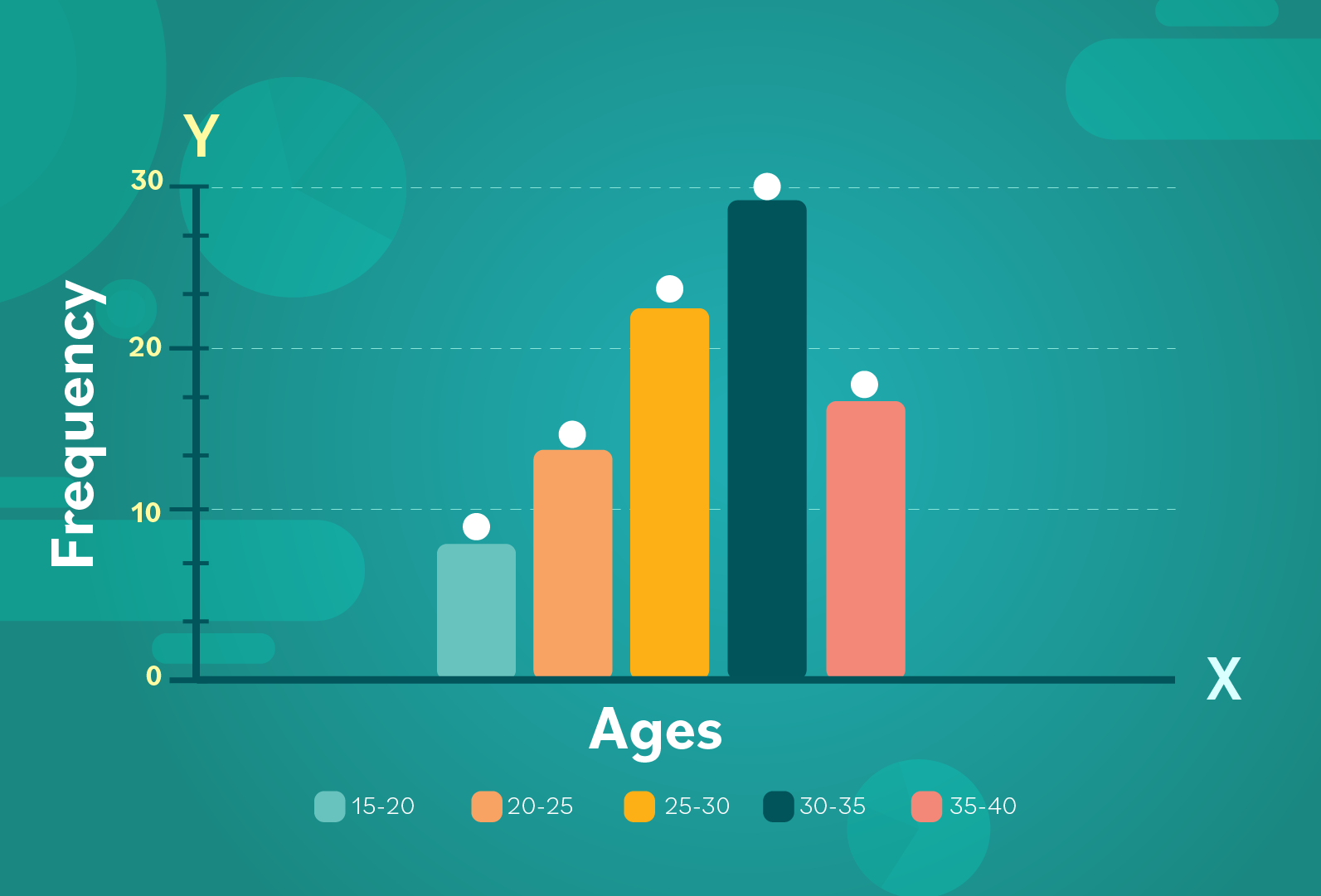
Each midpoint marked on the graph represents the frequency of each bin or age range.
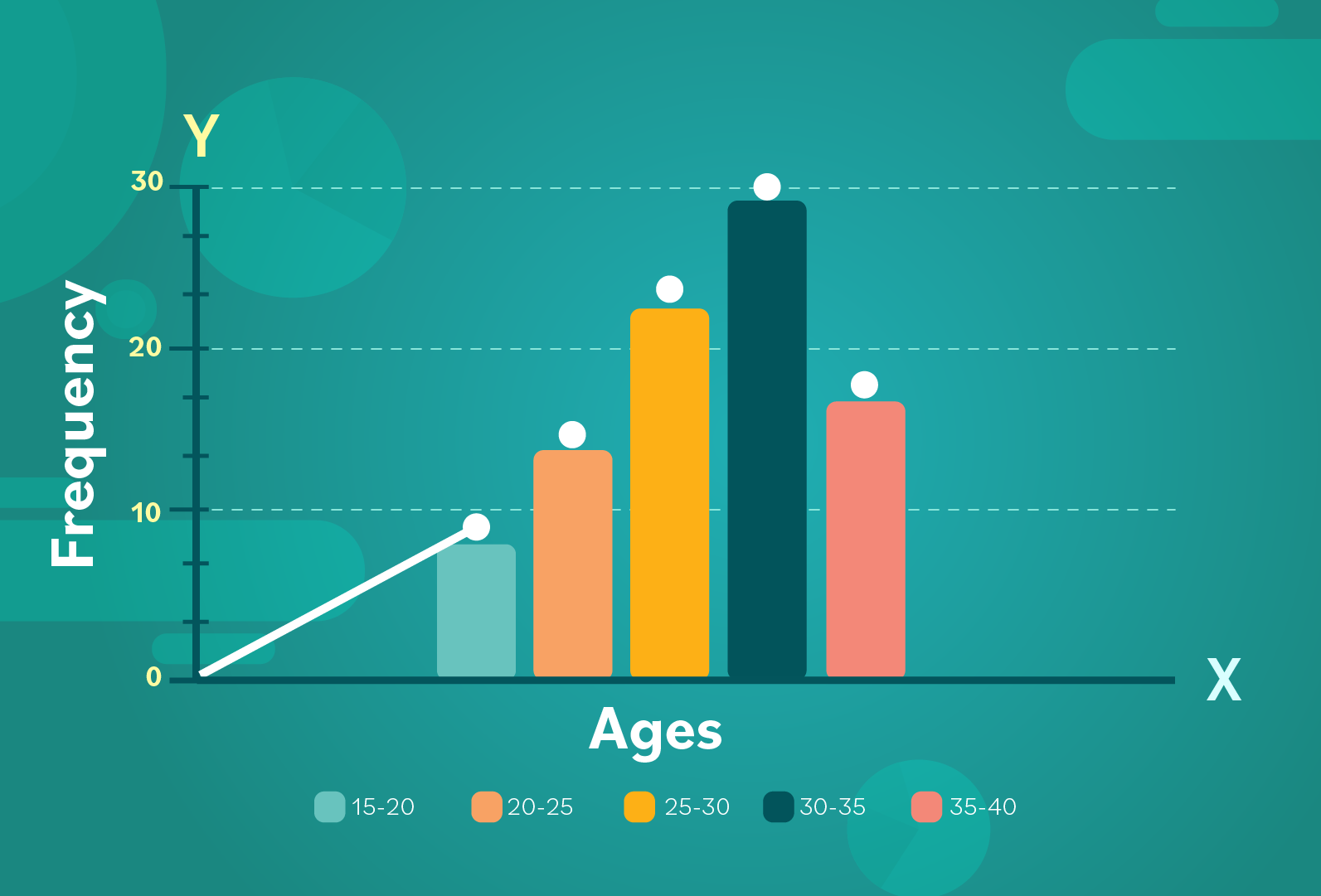
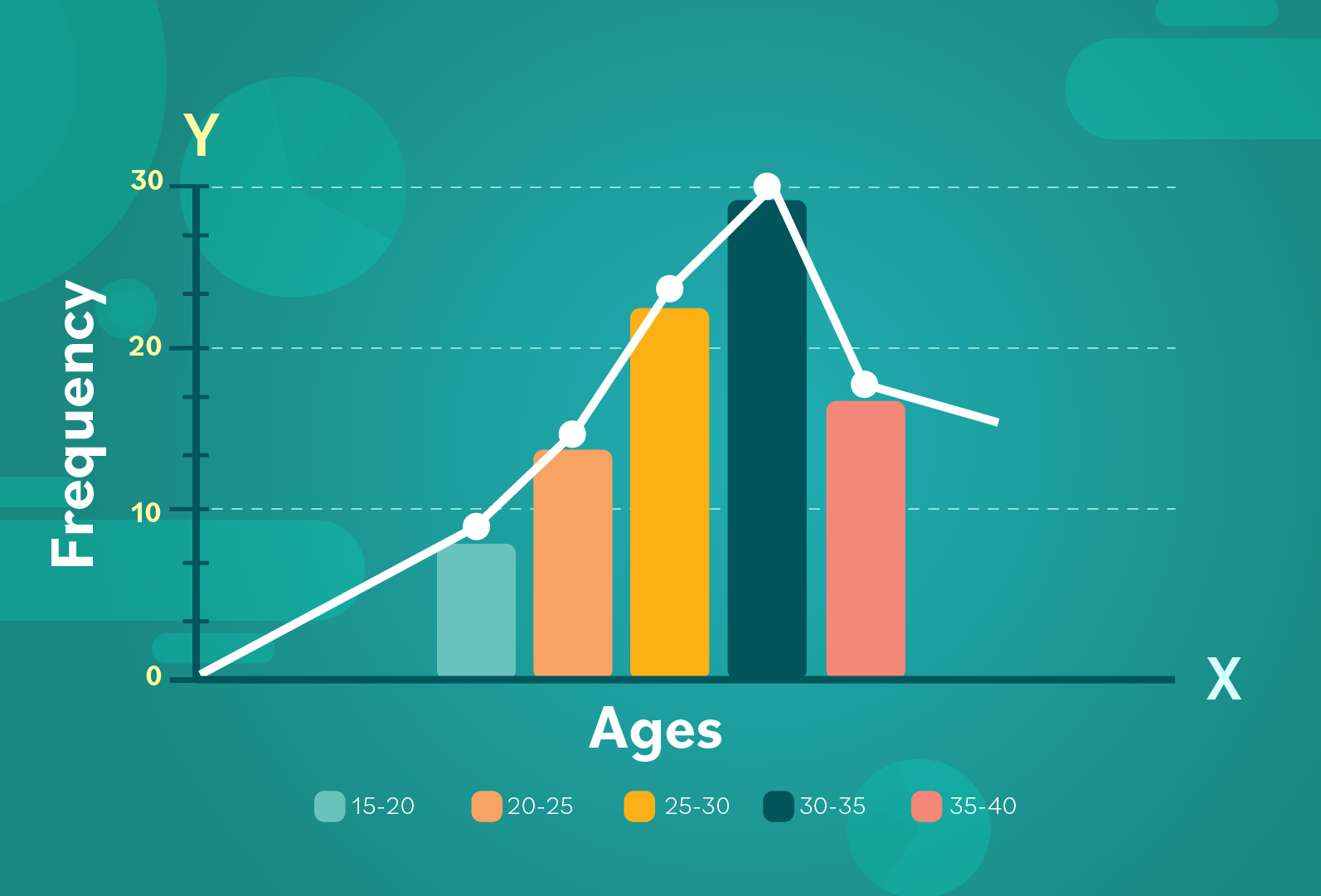
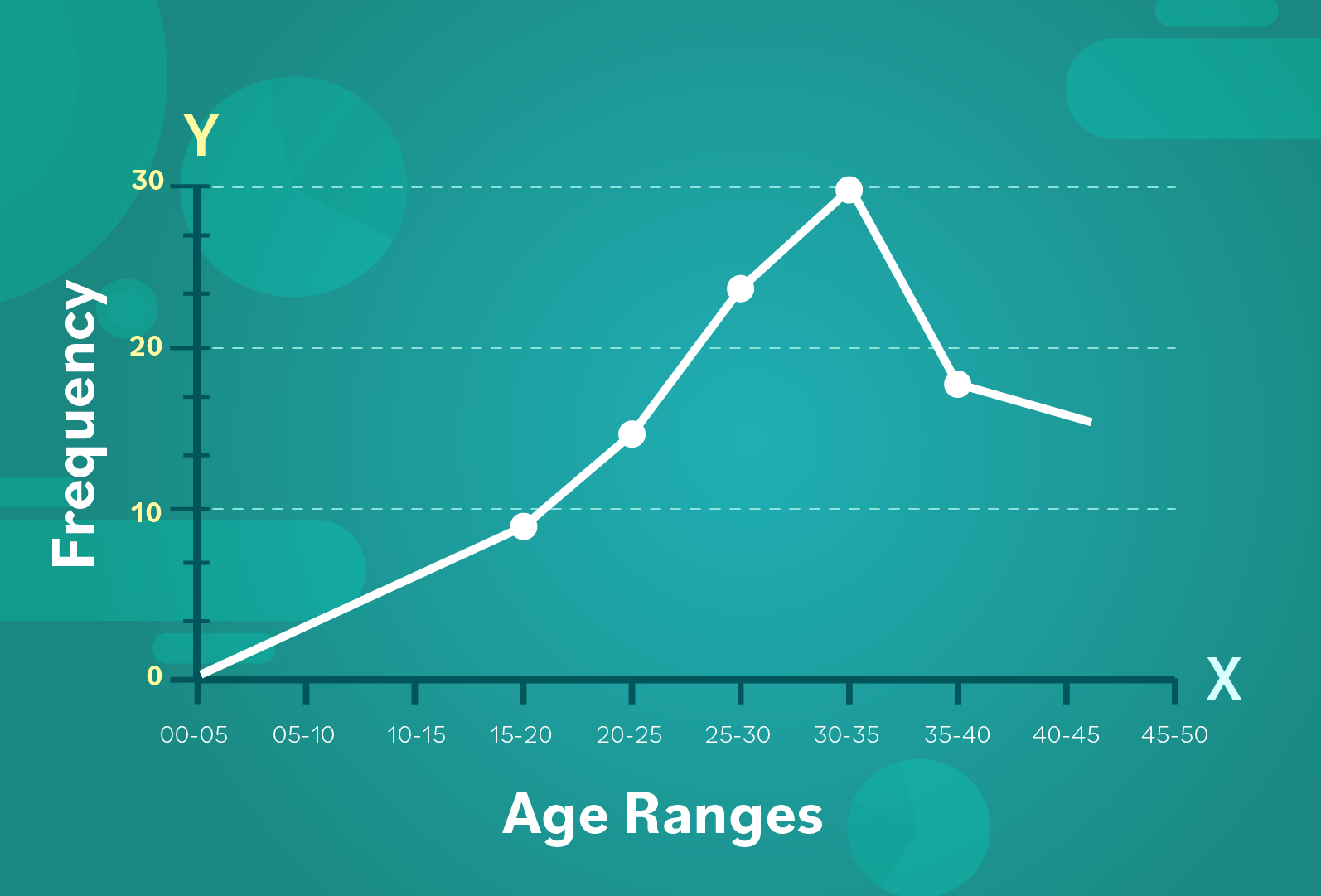
Usually a frequency polygon is compared to a different frequency polygon on the same graph. The second frequency polygon comes from another data set.
For example, if you wanted to compare the age range of the band’s members from 10 years ago with the current band, you could do two things:
You would plot your frequency polygons on the same graph. Let’s use a gray line to represent the data set from 10 years ago, which we can compare with the white line representing the current band’s ages:
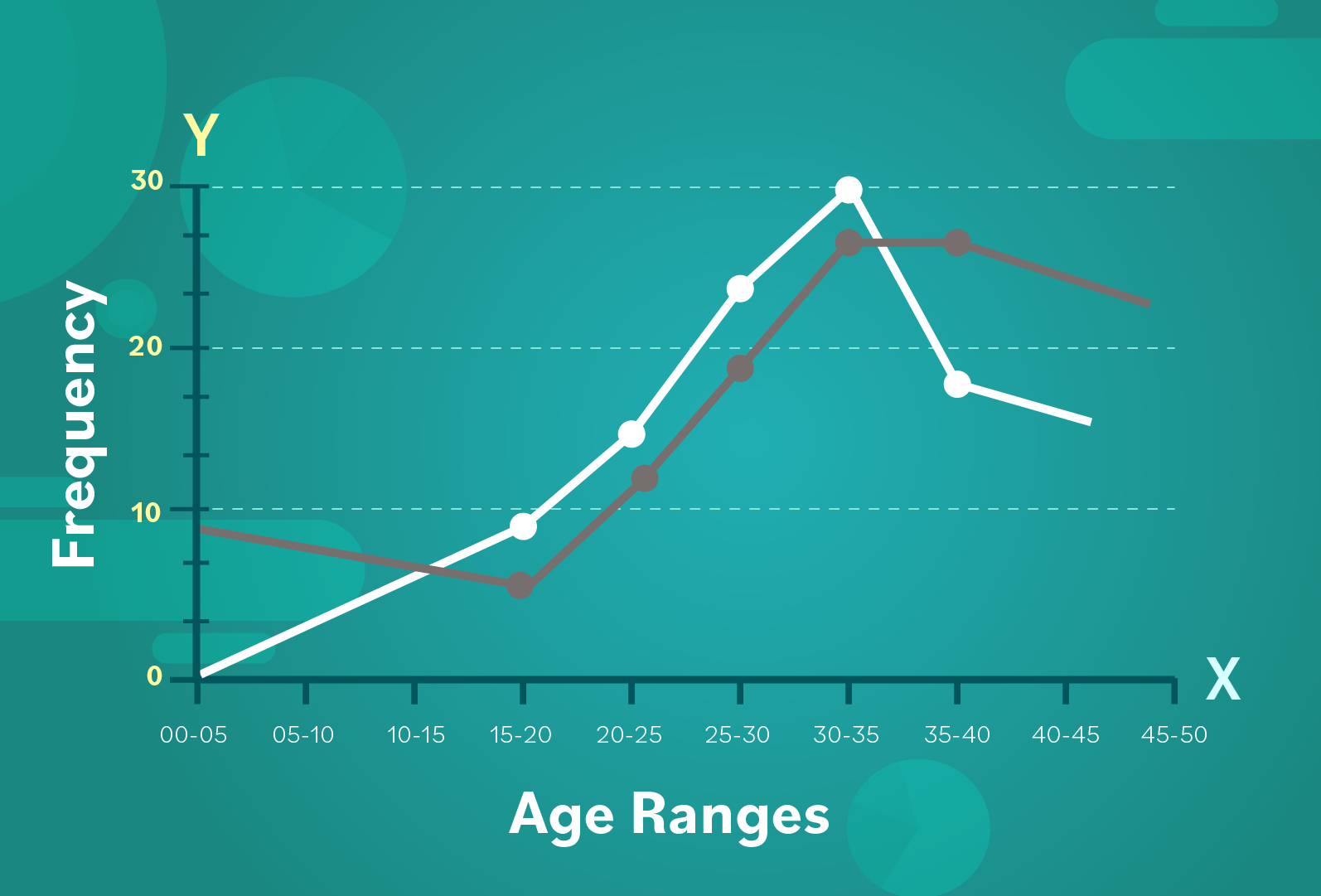
On the whole, the trends in the data appear quite similar. The conductor can see that there’s been a dip (or decline) in the 35-40 year age range.
Here’s a quick recap…
In the next section of the tutorial, we’ll start diving into some other fundamentals that will help you in statistics.
/en/statistics-basic-concepts/mean-median-and-mode/content/