Usando a matemática
Mas e se o sol fosse...


/pt/usando-a-matematica/como-eratostenes-mediu-o-tamanho-da-terra/content/
Se o sol fosse do tamanho de uma bola de basquete, a Terra seria do tamanho de uma pulga, e estaria orbitando em torno desta bola a uma distância de metros. A lua seria do tamanho de um grão de areia e giraria em voltada pulga a uma distância de cm.
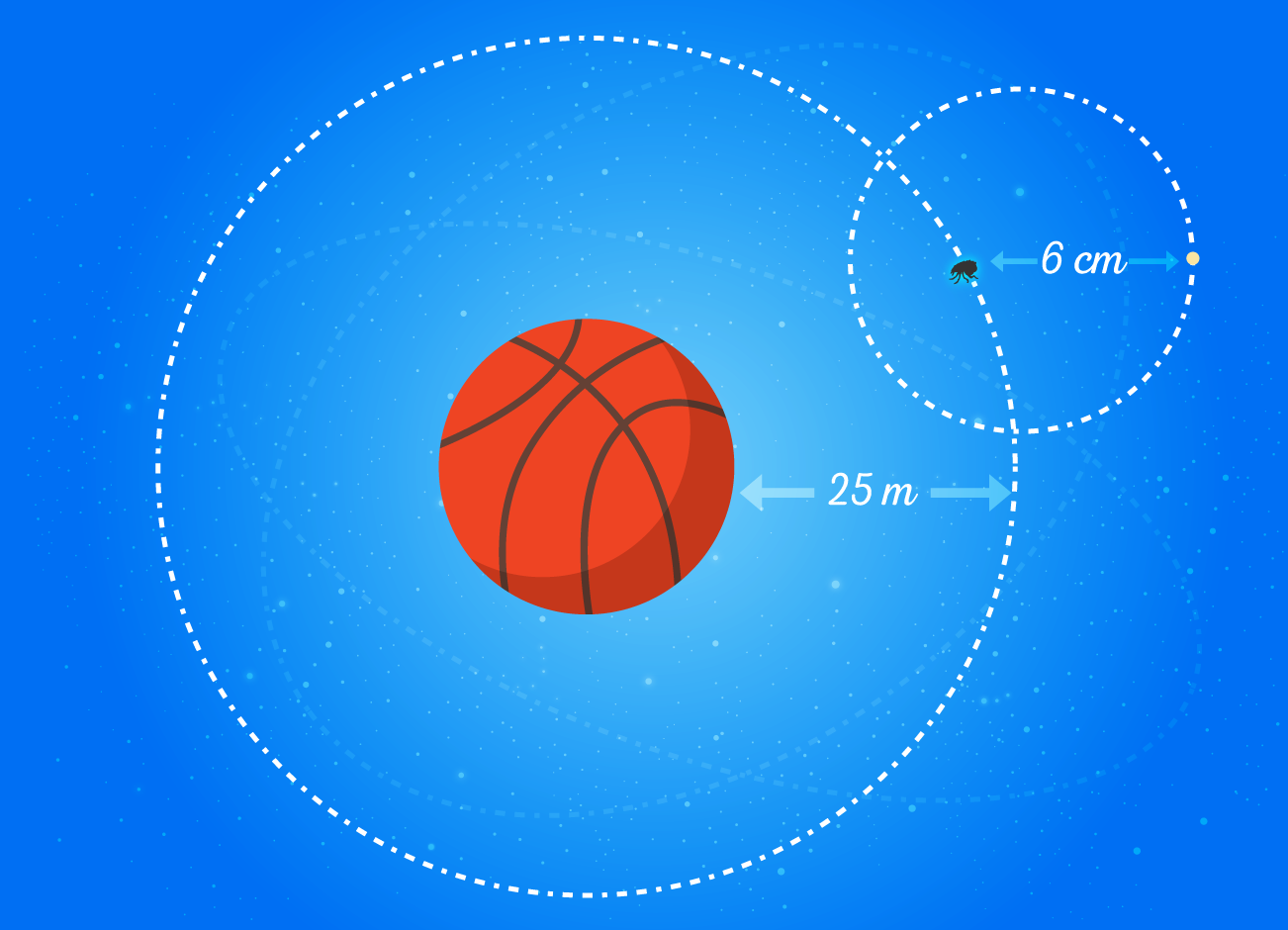
Acabei chegando a estas conclusões através do conceito matemático de proporção, porque com ele podemos fazer comparações para entender o nosso sistema solar. Para continuarmos, devemos primeiro entender o que são proporções.
Na matemática, uma razão é uma relação entre duas quantidades. Para poder calculá-la, devemos fazer a divisão entre elas, por exemplo, para calcular a razão entre os números e , temos que fazer a divisão: :
Como o resultado da divisão é, dizemos que a razão entre e é .
Para poder fazer as associações que fizemos no início, pegamos um objeto para comparar com o tamanho do sol que foi uma bola de basquete que tem centímetros. Em seguida, calculamos a razão entre o tamanho real, , e o tamanho fictício, considerando que são quilômetros:
Esta razão nos permite calcular o tamanho de outros corpos do sistema solar. Se queremos determinar o tamanho de um outro objeto, devemos escolher o mais adequado para que entre o tamanho real e o fictício tenhamos a mesma razão que acabamos de obter entre o sol e a bola. Vejamos por exemplo, qual tamanho deveria ter Júpiter: Sabemos o diâmetro real do planeta é: ; e para encontrar a razão, temos de encontrar um tamanho fictício desta forma:
Chamamos a igualdade entre duas razões de proporção. Para encontrar o número preciso basta dividir o tamanho real na razão:
Com base nesta última expressão, descobrimos que o tamanho fictício de Júpiter deve ser . Isto significa que se o sol fosse uma bola de basquete, Júpiter teria o tamanho aproximado de uma amora e giraria em torno da bola a uma distância de quase metros.

Desta forma, podemos dizer que, se o sol fosse uma bola de basquete, o planeta Mercúrio teria a espessura de uma agulha de seringa (cerca de ) e orbitaria a metros; Marte seria tão grande como a ponta de um lápis e estaria a quase metros da bola; Saturno, sem contar com seus anéis, teria o tamanho da boca de uma garrafa de plástico ( aprox.) e estaria a uns metros da bola; Plutão, seria um pouco menor que um grão de sal , e estaria a mais ou menos um quilômetro de bola. Você consegue imaginar? um grão de sal girando em torno de uma bola de basquete a mais de um quilômetro de distância.
Existe uma região do sistema solar chamada Nuvem de Oort, de onde se acredita que vem os cometas mais distantes. Esta região está localizada um ano-luz do nosso Sol, e se aplicarmos a proporção encontraremos que a Nuvem de Oort estaria a uns da bola.
Não é incrível que um objeto de de diâmetro exerça sua influência através do espaço vazio para percorrer uma distância maior do que a França e a Alemanha juntas? Isto é o que faz o sol, sua grande massa exerce influência sobre os objetos que estão a mais do que um ano-luz de distância.
Para terminar, quanto você acha que a bola de basquete está distante da estrela mais próxima? ... A resposta é , uma distância um pouco menor do que a do nosso Brasil de ponta a ponta que é .
Como você pode ver, as proporções são uma grande ferramenta para termos uma ideia do que é o nosso sistema solar, e esta é apenas uma das formas que podemos usá-las.
/pt/usando-a-matematica/por-que-existe-o-sistema-internacional-de-medidas/content/