/pt/somar-e-subtrair/soma-e-subtracao-de-inteiros-na-reta/content/
Ao fazer adições e subtrações podemos encontrar operações como esta: , que nada mais é que uma soma de dois números inteiros negativos, ou com algo assim: , que é a subtração entre um número natural e um inteiro negativo. Para resolver estas situações devemos considerar os sinais como nesta tabela:
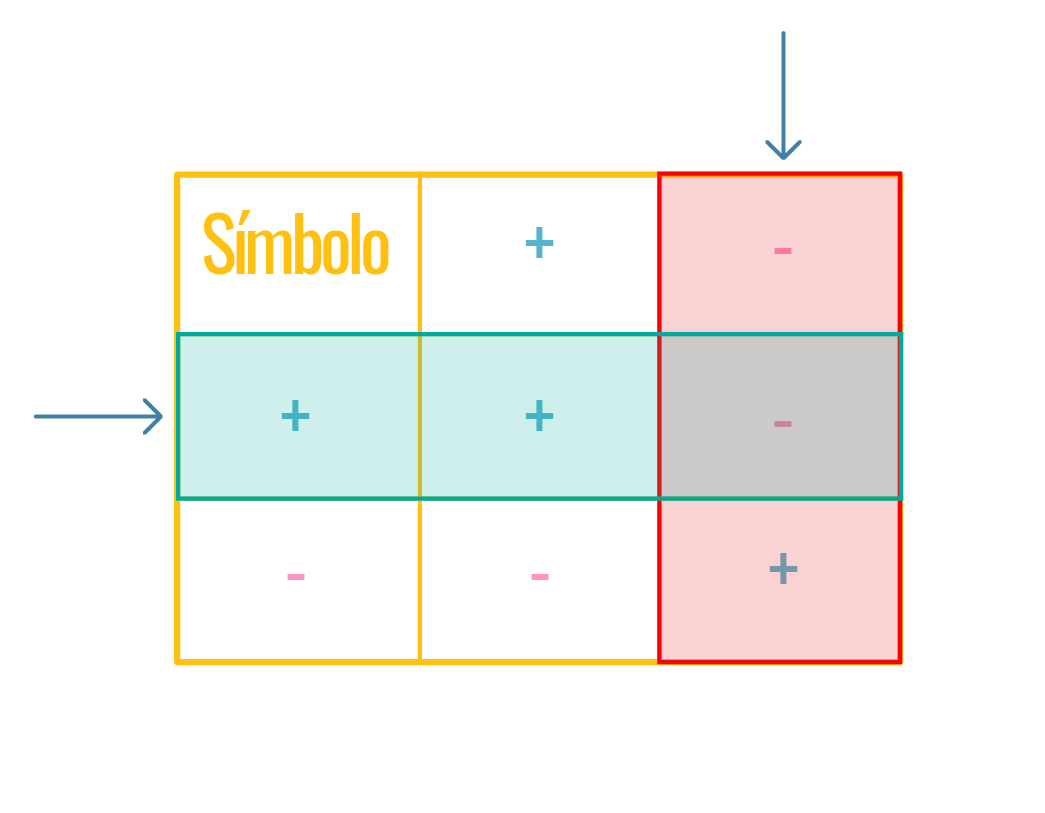
Quando encontramos dois sinais de positivo e/ou negativo consecutivamente, substituímos pelo sinal de que está no cruzamento da linha com a coluna.
Por exemplo, na expressão vemos dois sinais seguidos. Um mais e um menos. Assim localizamos na linha do mais e na coluna do menos, e observamos o sinal que mostra seu encontro. De acordo com a tabela acima e seguidos são equivalentes a menos, portanto, . Observe que é o mesmo que quando temos um parênteses: .
Em muitos países, a regra de sinais é chamada de multiplicação de sinais, no entanto, não podemos entender como uma multiplicação de números, é simplesmente uma maneira de chamar essas relações.
Com base nisso, seguindo as indicações da regras de sinais da tabela, podemos dizer que:
Outra maneira de se lembrar é pensando assim, a multiplicação de sinais iguais dá mais, e de diferentes dá menos.
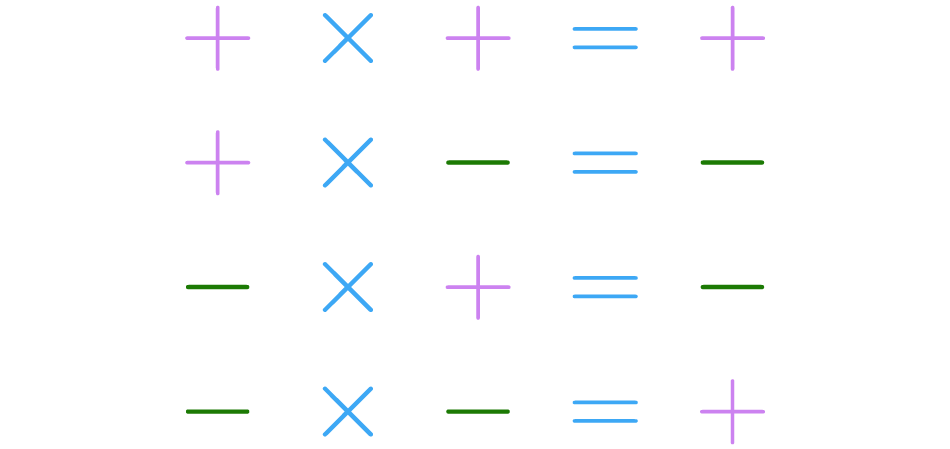
Suponhamos que é um número natural maior que zero: . A representação na reta numérica do deve ser com uma flecha apontando para a direita.
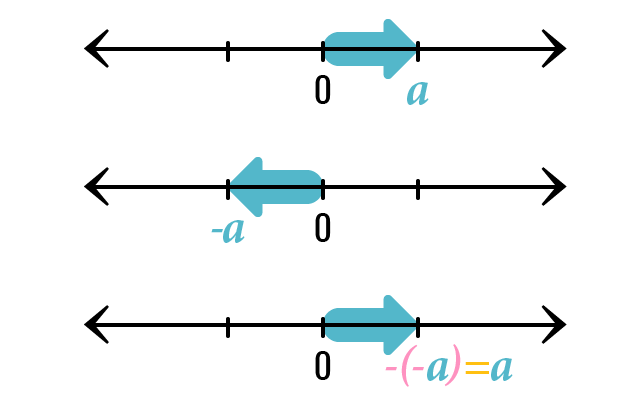
No entanto, se colocarmos um menos no número , obtemos o número , que é representado por uma flecha apontando para a esquerda. Observe que se colocamos um outro sinal de menos ao , graças a regra dos sinais obtemos porque .
Podemos dizer que quando um sinal de menos está antes de outro sinal, a flecha que representa o número em questão muda de sentido, mas quando o sinal de mais vem antes, o sentido da flecha não muda.
/pt/somar-e-subtrair/simplificacao-de-expressoes-com-regras-de-sinais/content/
