/pt/somar-e-subtrair/subtraindo-numeros-grandes/content/
As propriedades das operações nos ajudam a simplificar os cálculos e a entender melhor o que estamos fazendo, mas se aplicamos as propriedades incorretamente podemos cometer erros.
A propriedade associativa da soma nos diz que existem duas maneiras de realizar a operação entre três números e que o resultado será o mesmo. Para mostrar que a subtração não possui esta propriedade vamos usar um exemplo, considere a operação .
Faremos o seguinte cálculo . Em primeiro lugar, conforme está indicando os parênteses, efetuamos a subtração de e em seguida calculamos este resultado com o menos três desta forma: .
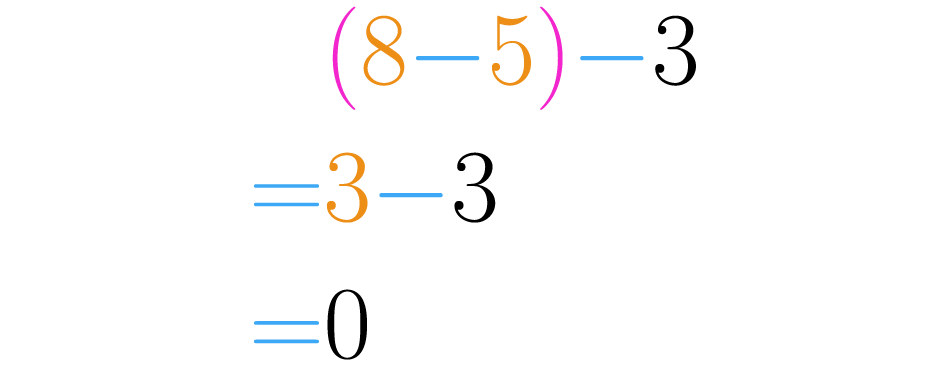
Agora vamos executar a operação iniciando pelos parênteses: , e então operamos este resultado com o oito desta forma: .
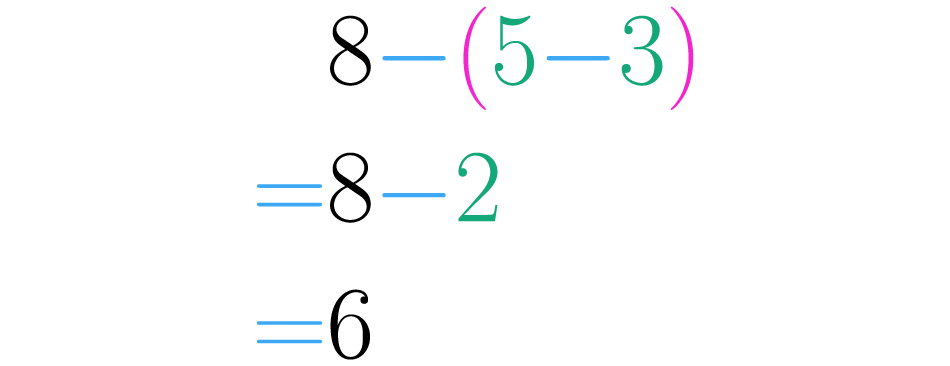
Como você pode ter percebido, calculamos nos dois casos os mesmos três números. No entanto, ao mudar a ordem das operações, o resultado também mudou. Por isso, dizemos que a subtração não possui a propriedade associativa, o que significa que você deve ter muito cuidado quando faz subtrações com vários números, não podemos realizar a subtração usando qualquer ordem.
No caso da soma, a propriedade comutativa diz que . Você acha que o mesmo acontece com a subtração: ? Consideremos os números e para fazer um teste:
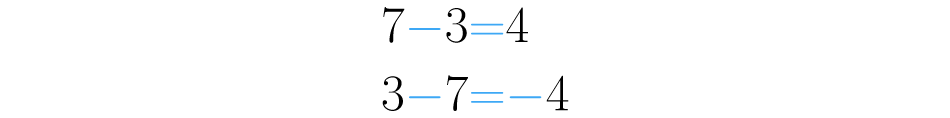
Como os resultados não são iguais, podemos assegurar que a subtração não possui a propriedade comunicativa porque, em geral, os resultados das subtrações e não são iguais.
/pt/somar-e-subtrair/resolvendo-problemas-com-subtracoes/content/
