/pt/somar-e-subtrair/somando-varios-numeros/content/

Propriedades da soma

Conhecer as propriedades da soma/adição lhe ajudará a entender melhor esta operação. Além disso, em alguns casos, também servem para simplificar as operações.

Propriedade associativa

Algumas vezes somamos três ou mais números. Se temos por exemplo, que fazer a soma ,  a propriedade associativa nos garante que podemos fazer esta operação de duas maneiras diferentes obtendo o mesmo resultado, observe:

Uma maneira é a seguinte: . Neste caso, os parênteses indicam que devemos primeiramente somar esses números: , e o resultado desta adição será somado ao terceiro número, .

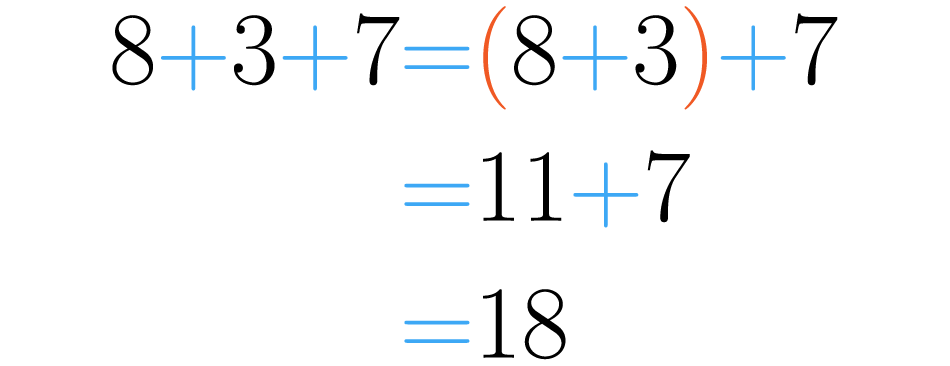
A outra maneira é assim: . Agora, os parênteses nos dizem que devemos primeiro fazer a soma de , e depois podemos somar ao primeiro número obtendo assim: .

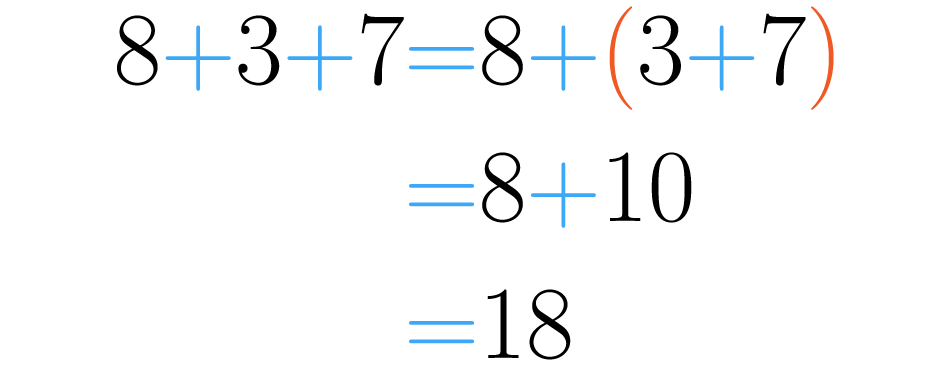
Como você pode perceber, em ambos os casos obtivemos como resultado de soma o . Isto não acontece apenas com os números oito, três e sete, acontece com todos os números! Para fixar esta ideia podemos enunciar a propriedade associativa assim: dado três números qualquer , e :

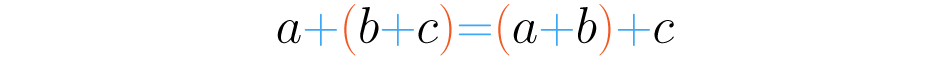
Através dos símbolos , e estamos representando todos os números de um modo geral. A propriedade associativa nos diz que quando somamos vários números, podemos associá-los na ordem que mais nos convém.

Propriedade comutativa

Você acha que o resultado de uma soma muda se trocamos a ordem das parcelas? Por exemplo, se fizermos as somas ou , você acha que os resultados serão diferentes?

A propriedade comutativa nos assegura que não importa a ordem que colocamos as parcelas porque o resultado da soma não vai mudar. Observe que e .

Assim como acontece com a propriedade associativa, esta também é aplicada à todos os números e podemos fixar essa ideia da seguinte forma: dado dois números e :

Propriedade modulativa ou do elemento neutro

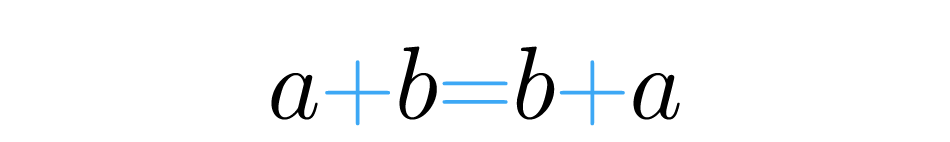
Esta propriedade é especial porque trata da existência de um número em particular, que não afeta os outros quando uma soma é realizada. Você conhece um número que adicionado a um, o resultado seja um? Ou que ao cinquenta e o resultado da soma seja de cinquenta? Bem, este número especial existe sim, se trata do zero, . Observe:

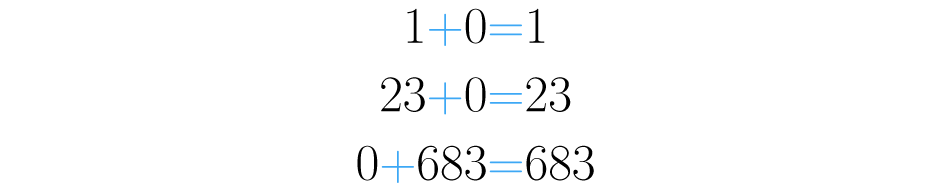
E assim podemos fazer com todos os números.

Poderíamos fazer isso com todos os números. Por isso dizemos que o zero é o elemento neutro da soma. Para fixar esta ideia, podemos escrever: dado qualquer número , temos:

Propriedade clausurativa

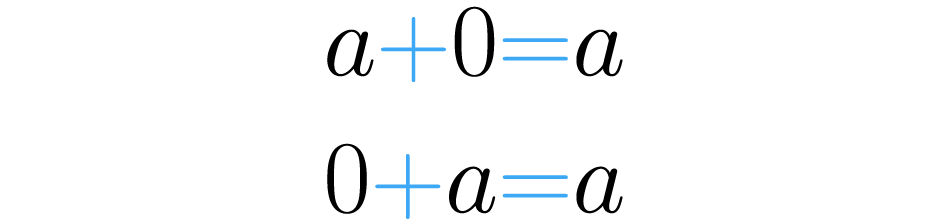
Para entender esta propriedade você precisa ter um conjunto de referência, neste caso aqui vamos usar os números naturais. Quando já tivermos um conjunto de referência, podemos nos perguntar se ao somar dois elementos desse conjunto (dois números naturais), o resultado da soma também pertence ao mesmo conjunto. Vejamos:

Vamos usar dois números qualquer do conjunto dos naturais, por exemplo, o e o . O resultado desta soma é , que também é um número natural.

Enclausurar significa fechar, por isso dizemos que a soma é fechada dentro do conjuntos dos naturais. De um modo geral para esta propriedade, dizemos que se e são dois números naturais, então também é.

A soma também é clausurativa nos conjuntos dos números inteiros, racionais, reais e outros.

/pt/somar-e-subtrair/problemas-que-podem-ser-resolvidos-com-somas/content/