Os conjuntos matemáticos
Tipos de conjuntos


/pt/os-conjuntos-matematicos/descrever-e-definir-conjuntos/content/
Existem vários tipos de conjuntos que se diferenciam conforme suas características. Conhecê-los nos ajuda a entender melhor sua estrutura e o mundo dos conjuntos.
Para evitar confusões, quando definimos um conjunto devemos especificar de onde estamos pegando os elementos que o compõe. Isto significa que deve existir uma base da qual retiramos os elementos, e esta base sobre a qual trabalhamos é chamada de conjunto universal. Usaremos sempre a letra para representar o conjunto Universal.
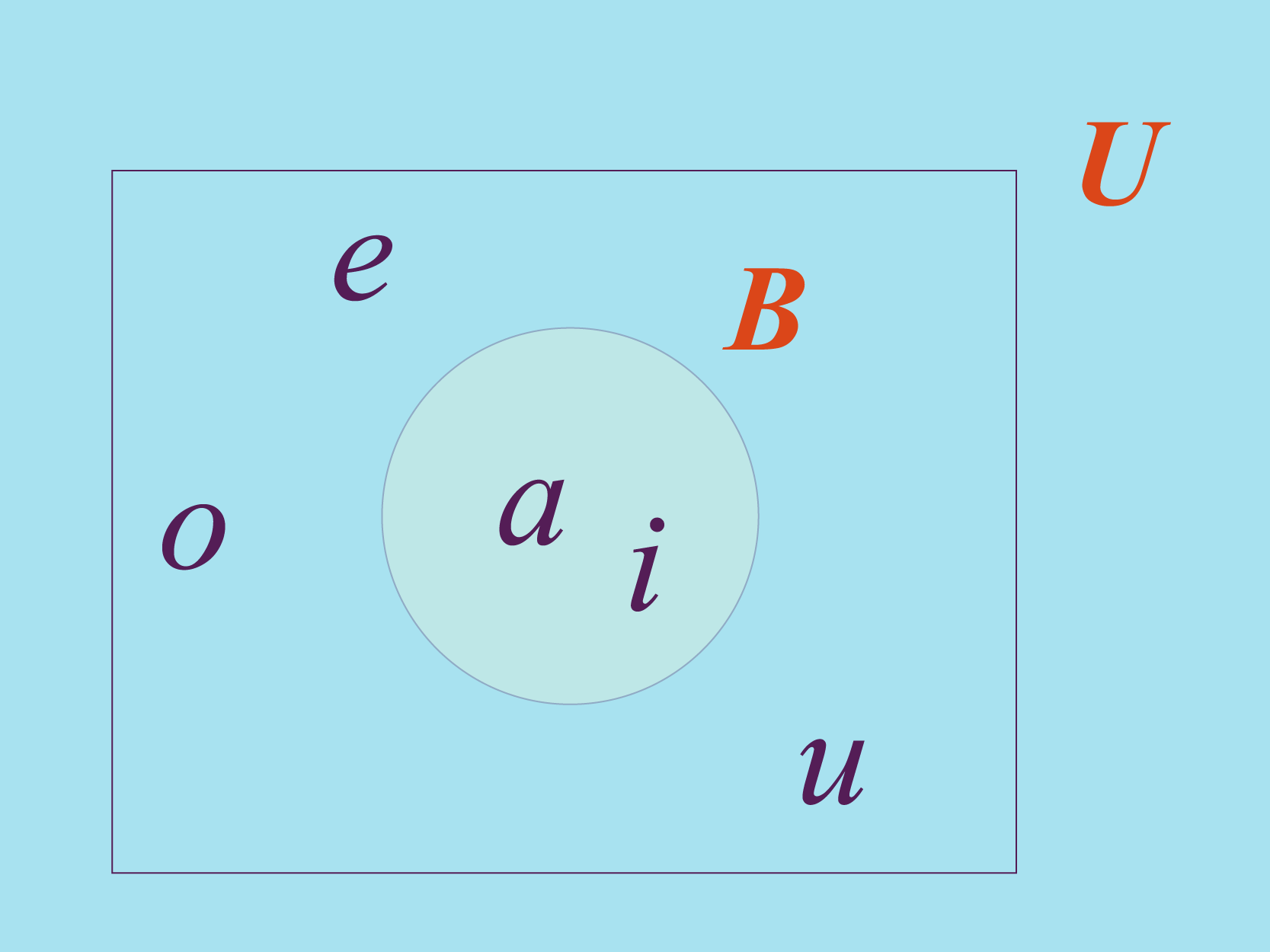
Se por exemplo, queremos definir como o conjunto formado pelas vogais e , o conjunto universal poderia ser o das vogais. Na figura acima mostramos como podemos usar os diagramas de Venn para ver a relação entre o conjunto e seu conjunto universal .
Observe que o conjunto universal pode ter exatamente os mesmos elementos de um determinado conjunto ou mais.
Um conjunto que não possui elementos é chamado de conjunto vazio. Para representar este conjunto usamos o símbolo de vazio, como mostrado na imagem abaixo.

Também, usando a descrição por extensão, representamos o conjunto vazio com as chaves .Como o conjunto vazio não possui elementos, não encontramos nenhum elemento dentro das chaves.
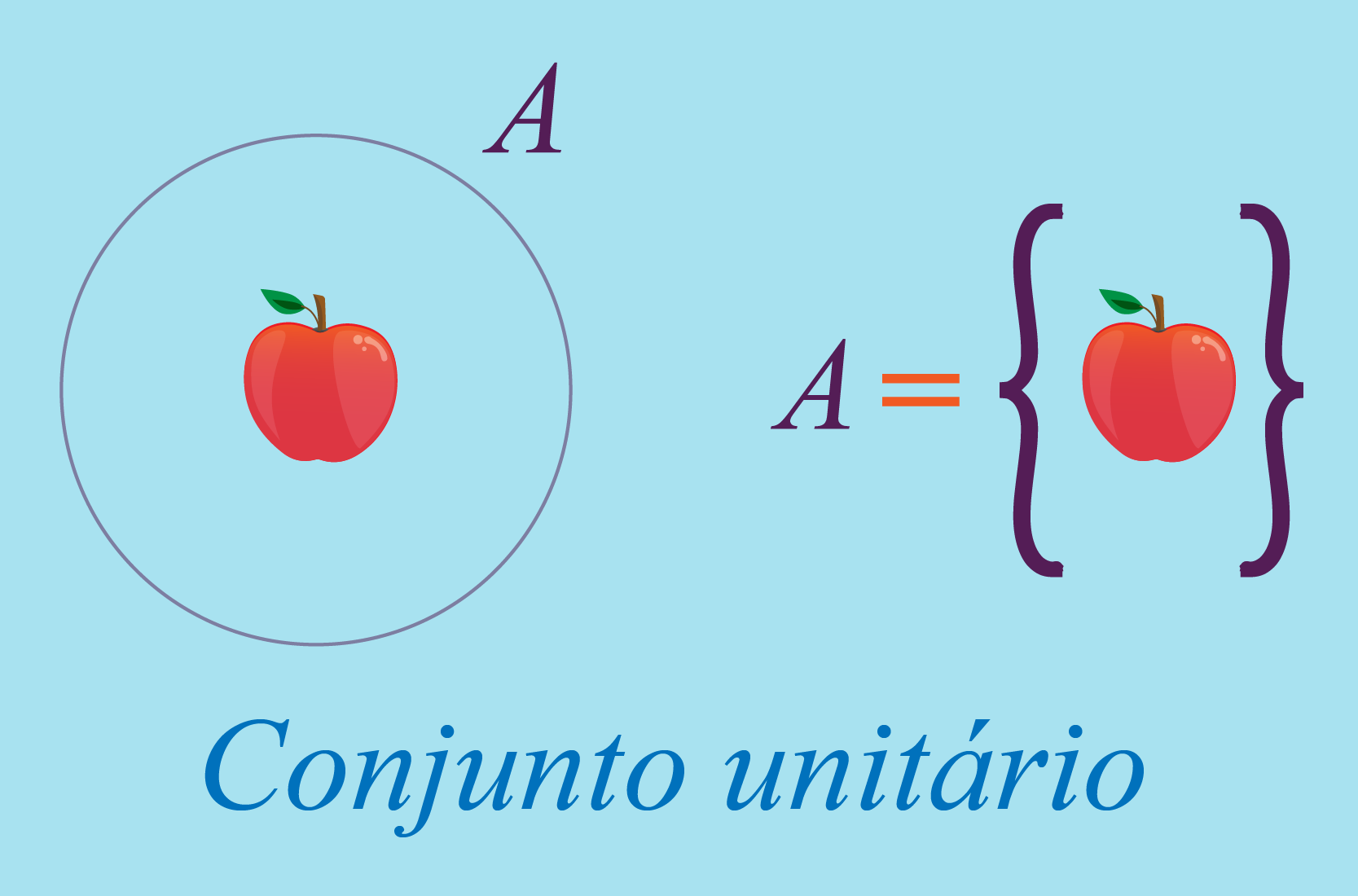
O conjunto unitário se diferencia por ter apenas um elemento. Não importa que tipo de elemento tenha pode ser um gato, um cachorro, um número, uma letra, ou qualquer outra coisa, se ele tiver apenas um elemento, o chamaremos de conjunto unitário.
Este tipo de conjuntos também se diferencia pela quantidade de elementos que possui. Um conjunto é finito se podemos contar todos os elementos que ele possui.
Por exemplo, o conjunto das letras do idioma português é finito porque possui 26 letras. Na imagem abaixo vemos um exemplo de um conjunto finito. Observe que os conjuntos unitários também são finitos.

Não é fácil encontrar na natureza exemplos deste tipo de conjunto. Os conjuntos infinitos são aqueles que não podemos contar a quantidade de elementos que o compõe. O método mais fácil de representar este tipo de conjunto é por compreensão. Basta portanto, mencionar as características que possui seus elementos para determinar todos eles. Consideramos o conjunto dos números que terminam em 3, poderíamos defini-lo assim:
Também existe uma forma de representar alguns conjuntos infinitos por extensão. Basta exibir os primeiros elementos do conjunto e indicar com três pontos que a lista continua indefinidamente. No caso do conjunto , que vimos no parágrafo anterior e que é formado pelos números que terminam em três, temos
Os exemplos mais simples e comuns de conjuntos infinitos são os compostos por números. Quantos números pares existem? Quantos múltiplos o número três possui? Estes conjuntos são infinitos e isso não é porque não temos a capacidade de contar a quantidade de elementos que eles têm, mas porque é impossível contar já que não há um número que representa a quantidade de elementos que o conjunto possui.

Não devemos confundir os conjuntos infinitos com conjuntos finitos que possuem uma grande quantidade de elementos, por exemplo, você acha que o conjunto de grãos de areia da terra é um conjunto infinito? Neste caso, ainda que o conjunto tenha uma enorme quantidade de elementos, deve existir um número que o represente, mesmo que este número seja gigantesco.

/pt/os-conjuntos-matematicos/conjuntos-equipotentes/content/