Os conjuntos matemáticos
Conjuntos Equipotentes


/pt/os-conjuntos-matematicos/tipos-de-conjuntos/content/
Quando falamos de conjuntos Equipotentes, os comparamos e estabelecemos relações entre eles. Veja do que se trata este conceito:
Dizemos que dois conjuntos são equipotentes quando estão formados pela mesma quantidade de elementos. Por exemplo, suponhamos que em uma festa de aniversário exista a mesma quantidade de taças de vinho e de convidados.
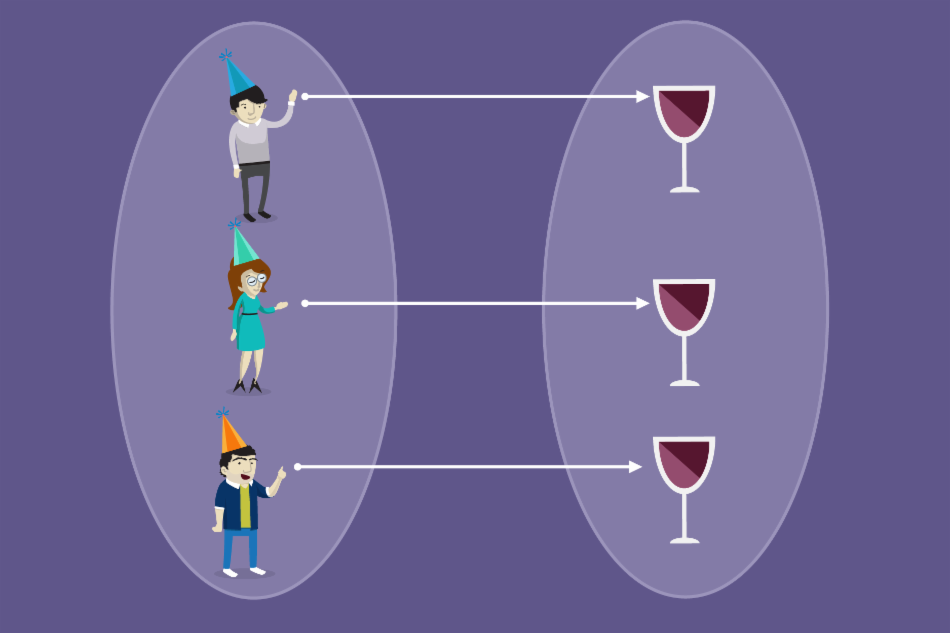
A forma correta de saber se dois conjuntos são equipotentes ou não, é estabelecendo uma relação entre seus elementos. Esta relação deve ter algumas características especiais que vamos explicar a seguir.
Vamos supor que precisamos saber se o conjunto e o conjunto são equipotentes, e para isso, as condições abaixo devem ser cumpridas na relação entre estes dois conjuntos:
Se uma relação entre conjuntos possui estas condições, é chamada de relação um a um. Na imagem anterior por exemplo, cada convidado está relacionado com uma taça, e cada taça está vinculada a um convidado.
Quando é possível estabelecer uma relação um a um entre os conjuntos e , dizemos que é equipotente de . Caso ocorra o contrário, dizemos que não são equipotentes.
Deve ficar claro que a equipotencia não é uma característica de um conjunto, mas uma relação entre dois conjuntos. Por exemplo, não é correto dizer que o conjunto é equipotente. A expressão adequada é: os conjuntos e são equipotentes.
Observe que se os conjuntos não têm a mesma quantidade de elementos eles não são equipotentes: imaginemos que agora chegou na festa uma pessoa que não foi convidada. Podemos estabelecer a seguinte correspondência entre os conjuntos:
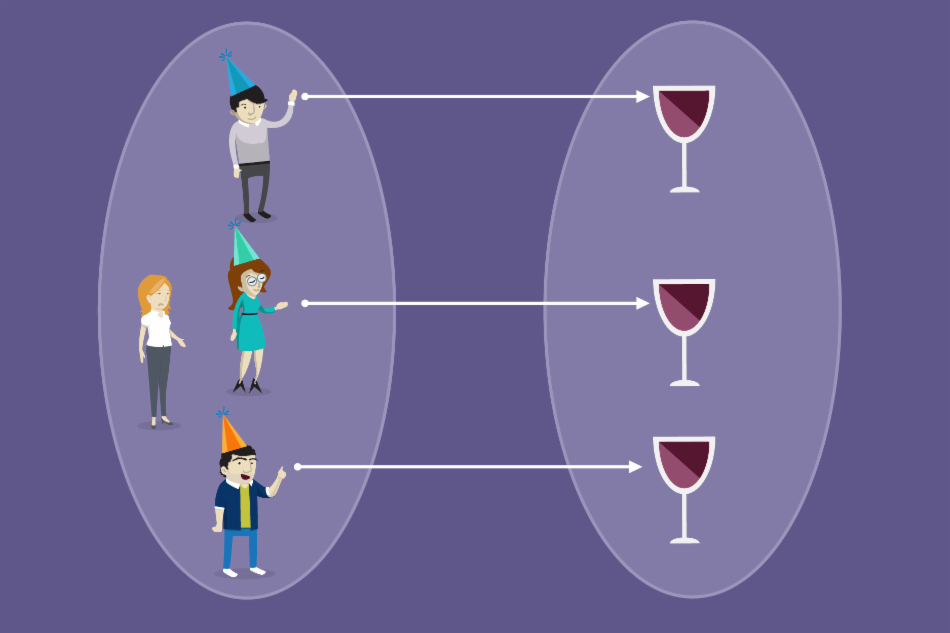
Como você deve ter percebido, a primeira condição não deu certo, porque cada elemento do conjunto de convidados deve estar relacionado com um único elemento do conjunto de taças. No caso exemplificado acima, esta relação não está dando certo, pois existe um convidado que não está se relacionando com uma taça. Agora nossos conjuntos não são equipotentes.
Se tentarmos dar um jeito nesta situação relacionando a pessoa que acabou de chegar com uma das taças que tínhamos disponíveis teremos a seguinte relação:
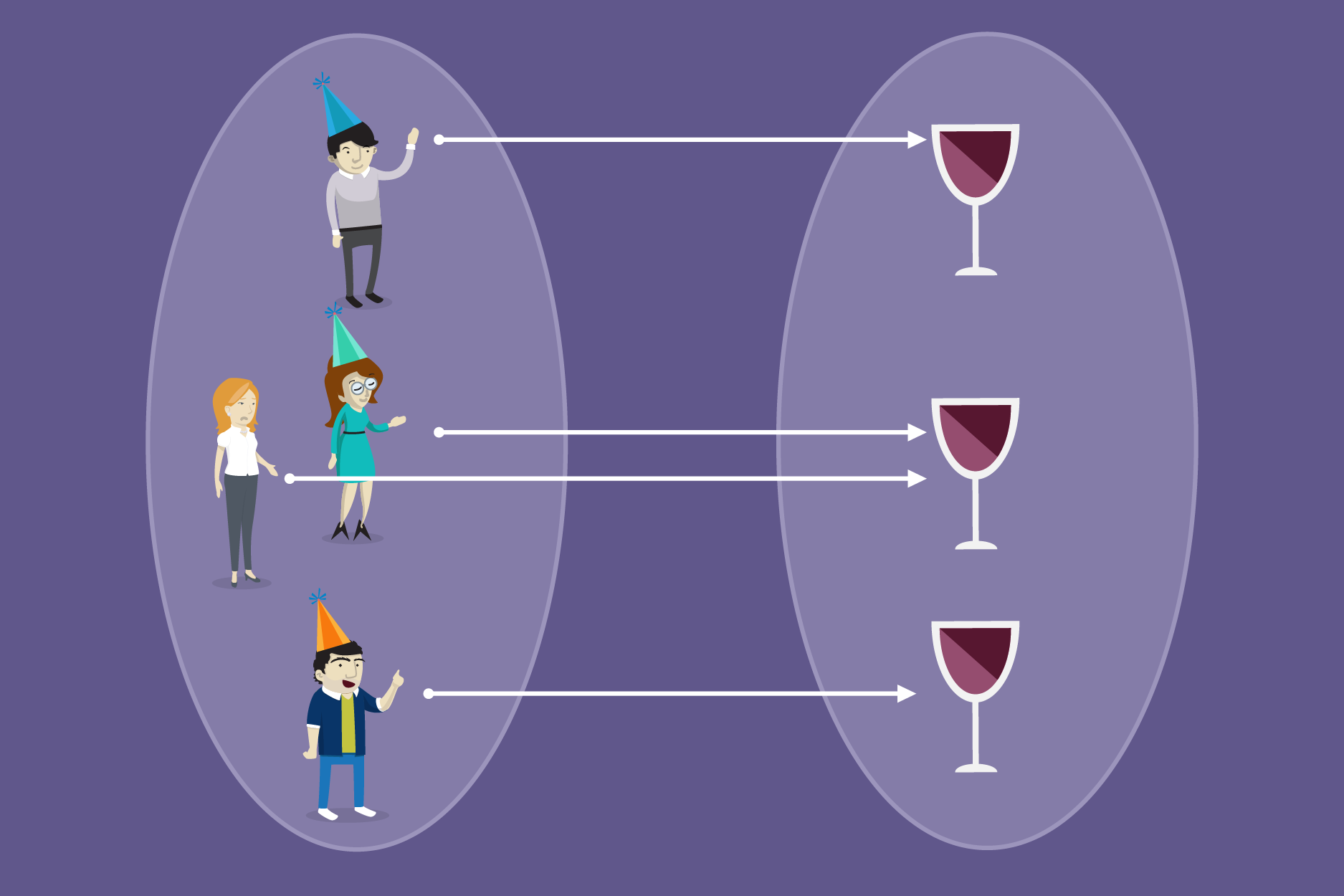
Observe que agora a condição que não dá certo é a segunda, isso porque cada elemento do conjunto de taças deve estar relacionado com uma única pessoa do conjunto de convidados e, neste caso isto não é o que está acontecendo porque tem uma taça que está relacionada com duas pessoas.
/pt/os-conjuntos-matematicos/relacoes-entre-conjuntos-e-elementos/content/