Los números
Algunas propiedades del conjunto de los números racionales


/es/los-numeros/que-son-los-numeros-racionales-o-fraccionarios/content/
El conjunto de los números racionales tiene propiedades distintas a las de los números naturales o a las de los números enteros, aprende cuáles son.
Sabemos que los números racionales son expresiones de la forma en donde y es distinto a cero. Veremos ahora como los naturales y los enteros pueden ser descritos también así:
Observa que es posible escribir cada número natural de la forma antes mencionada. Por ejemplo el uno: . Además , por lo tanto .
De la misma forma encontraremos que todo número natural es también fraccionario. Por ejemplo: , quince unidades distribuidas en tres partes iguales da un total de cinco unidades. Esto quiere decir que , puesto que .
Podemos asegurar por lo tanto que es un subconjunto de : .
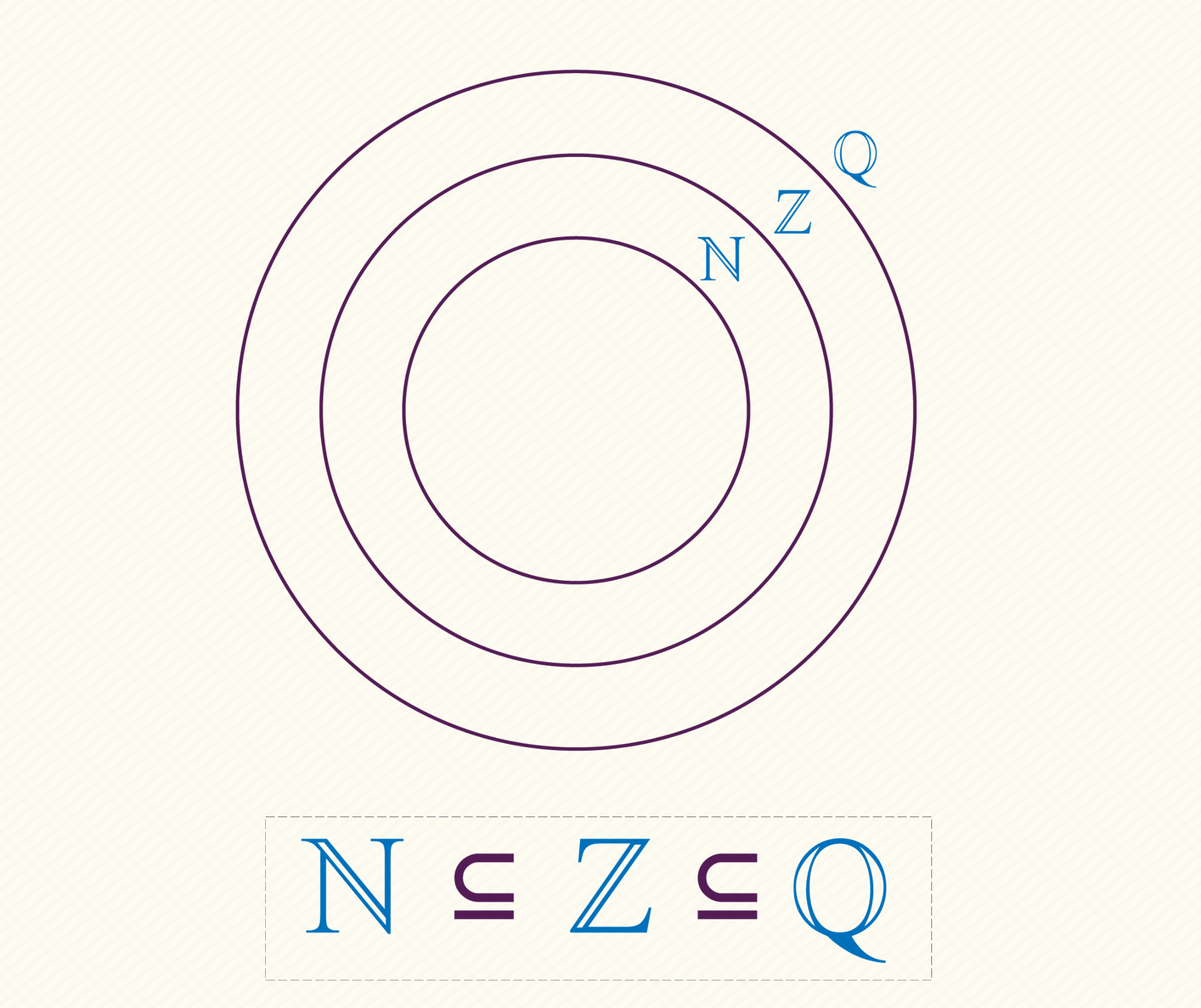
Una vez que hemos obtenido los números naturales como fracciones, es fácil obtener también los enteros. Por ejemplo: por lo tanto . Podemos resumir las relaciones de contenencia entre los conjuntos numéricos que conocemos como se muestra en la imagen de arriba.
Cada vez que definimos nuevos conjuntos ganamos en el número de operaciones que podemos realizar, esto sucedió también con los conjuntos y .

En el conjunto de los números naturales podíamos realizar la suma y la multiplicación; en el conjunto de los números enteros la suma, la multiplicación y la resta; en el conjunto de los racionales o fraccionarios tenemos los símbolos necesarios para poder representar también el resultado de las divisiones.
Cada vez que sumemos, restemos, multipliquemos o dividamos números racionales, obtendremos como resultado otro número racional.
Esto quiere decir que finalmente tenemos un conjunto en el cual todas las operaciones básicas están bien definidas.
¿Crees que dado un número racional es posible encontrar el siguiente? Fijemos las ideas: ubiquémonos en un número racional, por ejemplo el . ¿Cuál número racional es el siguiente al cero? Si estuviéramos restringidos a o , el sucesor sería simplemente , sin embargo, en el conjunto de los números racionales podemos representar fracciones de unidad.
Lo anterior quiere decir que para encontrar el sucesor del cero debemos buscar la expresión del tipo que represente la parte de unidad más cercana a cero, que representa no tener nada.
Representemos las unidades con círculos. Si partimos una unidad en dos partes iguales debemos representar cada una de ellas con la expresión , si la partimos en tres, con la expresión y así sucesivamente.
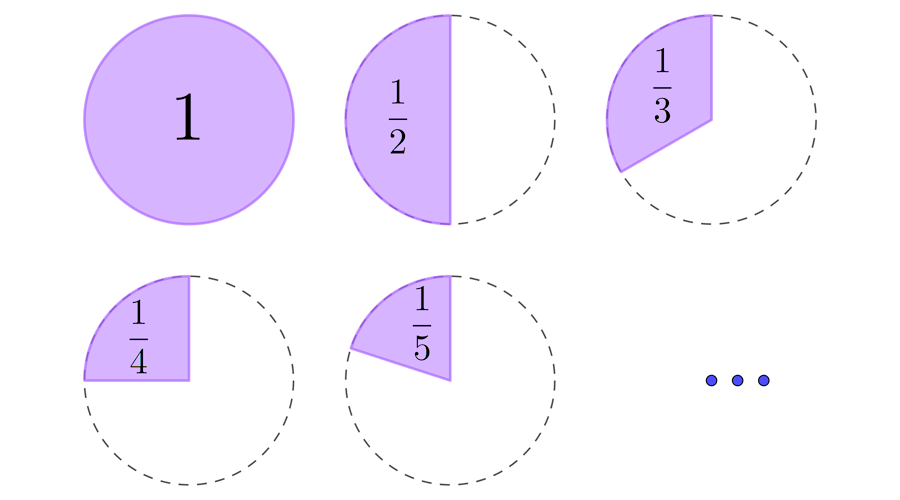
En la figura anterior puedes ver las partes de unidad que representan las fracciones y resaltadas con color. Como te puedes dar cuenta, entre más partes se divide la unidad, más pequeñas resultan cada una de las partes. Las expresiones , , etc. representan partes aún más pequeñas.
Entonces... ¿cuál es el sucesor del cero? ¡No existe! Los números fraccionarios no tienen sucesor; es decir, si nos ubicamos en cualquier racional no existe uno que siga sin que no haya más entre estos. Cada vez que escojas dos números racionales cualesquiera, por más cercanos que sean, encontrarás que entre ellos existen infinitos.
/es/los-numeros/orden-en-el-conjunto-de-los-numeros-racionales/content/