/es/los-decimales/problemas-con-division-de-decimales/content/
Cuando se trabaja con decimales, estos pueden llegar a tener muchas cifras en su cola decimal. Sin embargo, en la vida cotidiana, no tiene sentido trabajar con todas estas cifras, pues de cierto punto en adelante estas representan partes tan pequeñas, que no afectará si se las quitamos.
Existe un método para aproximarlos de la forma más precisa posible, es llamado redondeo. Observa el siguiente ejemplo:
Al realizar ciertos cálculos para la construcción de un edificio, un ingeniero obtiene que necesita kilos de concreto. Sin embargo, será suficiente nivel de precisión que este número tenga solo tres cifras decimales. ¿Cuál debe ser la aproximación?
Para hacer el redondeo nuestro amigo ingeniero debe realizar los siguientes pasos:
Se deben apartar las cifras decimales requeridas. En este caso se pide que sean tres.
Si la siguiente cifra a la derecha de las requeridas es mayor o igual que cinco, el último dígito requerido se aumenta una unidad. Si el número a la derecha de las cifras requeridas es menor que cinco, las última cifra requerida no cambia
En este caso, la siguiente cifra a las requeridas es un seis. Como seis es mayor que cinco, el ocho se transforma en un nueve, y el resto de cifras decimales se elimina.
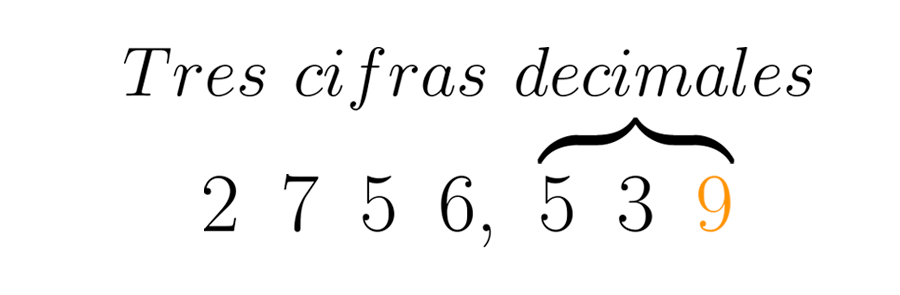
El ingeniero puede ahora trabajar con un número mucho más sencillo que el de antes: .
Es necesario hacer una aclaración: el número no es igual a . Es simplemente un número que se puede considerar lo suficientemente cerca al original. Para representar esta relación se usa el símbolo aproximadamente así:
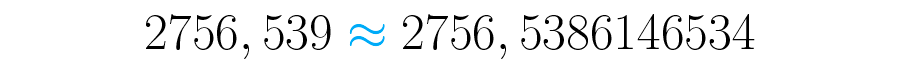
Que se lee: “ es aproximadamente igual a ”.
Observa como se aproxima el número a dos cifras decimales:
Se deben apartar las cifras decimales requeridas, que en este caso son dos:
Recuerda que el número que determina la aproximación es el siguiente a la derecha de las cifras requeridas, esta vez un cuatro.
Como la siguiente cifra a la derecha de las cifras requeridas es menor que cinco: , se dejan las cifras requeridas tal y como están, pero se elimina el resto:
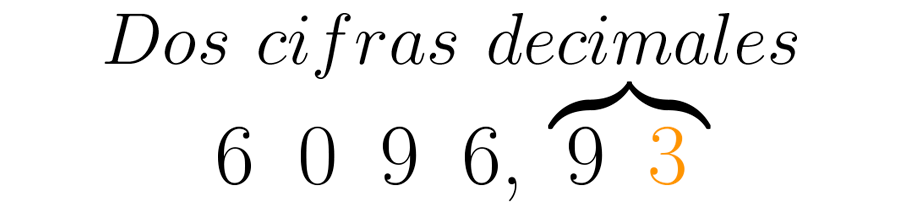
Se puede afirmar entonces que es aproximadamente igual a . De esta forma, cuando necesites trabajar decimales en tu vida cotidiana, podrás hacerlo con el nivel de precisión que cada situación amerita.
/es/los-decimales/decimales-para-medir/content/
