Divisores y múltiplos
Propiedades del máximo común divisor


/es/divisores-y-multiplos/propiedades-de-los-divisores/content/
El máximo común divisor, o , también goza de propiedades útiles. Conócelas aquí:
Para comprender esta afirmación tomemos como ejemplo los números y . El máximo común divisor de y es .
Si se multiplican estos dos números por tres: y también su se multiplica por tres. Así, .
Para comprobarlo hacemos las descomposiciones primas de y .
Los factores comunes son y , así que como lo asegura esta propiedad.

Lo mismo sucede si se dividen los números. Por ejemplo, y : , Si se dividen los números, por ejemplo en su también se divide en : .
y . En la siguiente imagen puedes observar las descomposiciones primas de estos dos números. Recuerda que si no hay factores primos comunes el es igual a .
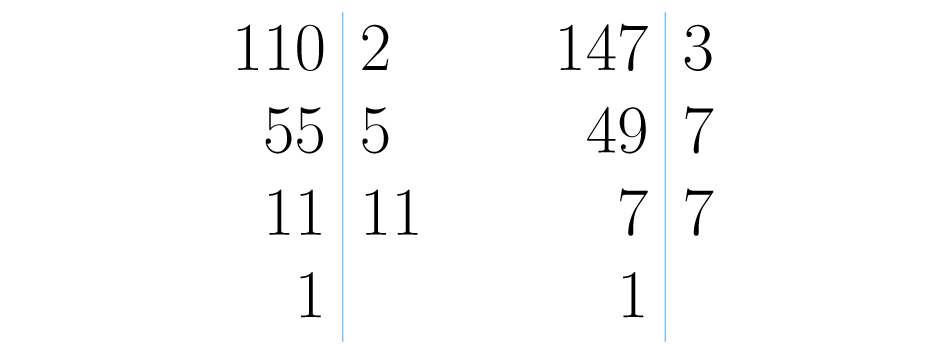
Como se puede concluir que son primos relativos, tal y como lo dice esta propiedad.
Al realizar las descomposiciones primas de los números, obtenemos el resultado mostrado en la siguiente imagen.
El será la multiplicación de los factores primos comunes, en este caso .

/es/divisores-y-multiplos/problemas-que-se-pueden-resolver-con-divisores/content/