Divisores y múltiplos
Descomposición en factores primos


/es/divisores-y-multiplos/los-numeros-primos/content/
Hay quienes dicen que los números primos son los ladrillos de la matemática. Aprende el porqué.
Para que comprendas que significa descomponer un número en factores primos debes recordar el significado de la palabra factor: un término que está multiplicando. Por ejemplo, en la expresión , cuatro es factor de cinco, y cinco es factor de cuatro, ya que cada uno está multiplicando al otro. ¿Nada más sencillo verdad? Ahora podrás comprender más profundamente que significa factorizar un número.
Es posible representar veinte unidades, por ejemplo, de varias formas: , ó son algunas de ellas. Pero ¿se puede escribir en factores? Es decir, ¿se puede escribir veinte representado como una multiplicación de números enteros? Claro: , por lo tanto se dice que es una factorización de . Factorizar un número es encontrar una forma de escribirlo como multiplicación. Observa que los factores son precisamente divisores del número.
Esto tiene sentido solo para números compuestos, pues para los números primos la descomposición es trivial. Por ejemplo, las únicas factorizaciones posibles de son: y .
Como te podrás imaginar, se puede factorizar (o descomponer) un número de muchas formas distintas.
Tomemos como ejemplo el número . En la siguiente imagen puedes observar algunas de las formas en las que es posible descomponerlo.
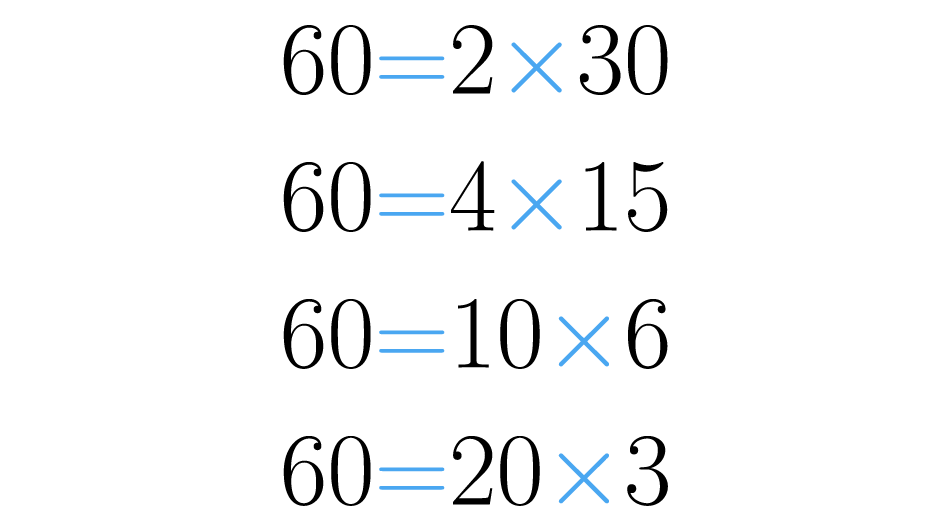
Recuerda que los números primos son aquellos mayores que uno, que tienen solo dos divisores: uno y ellos mismos. Los demás números, los compuestos, tienen varios divisores. Por esta razón siempre podremos descomponer los números hasta que cada uno de sus factores sea primo. Observa:
Tomemos una de las factorizaciones del número , por ejemplo . Observa que seis y diez son números compuestos, pues y .
Lo anterior quiere decir que se pueden descomponer seis y diez en más factores, por ejemplo: y . Por lo tanto la descomposición de se transforma así:
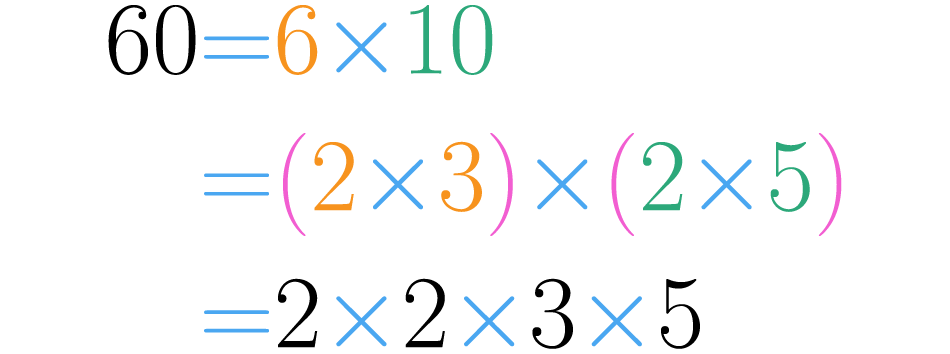
Usando las propiedades conmutativa y asociativa de la multiplicación, podemos escribir la descomposición de menor a mayor y sin paréntesis, como lo indica la última igualdad de la imagen anterior.
Ahora cada uno de los factores en la descomposición de es un número primo, y como estos no tienen más divisores que uno y ellos mismos, no es posible seguir transformándola, salvo por el orden.
Fíjate en que si se hubiera comenzado por otra descomposición de , se llegaría al mismo resultado.
Observa que la única diferencia entre esta descomposición y la obtenida anteriormente, es el orden de los factores primos.
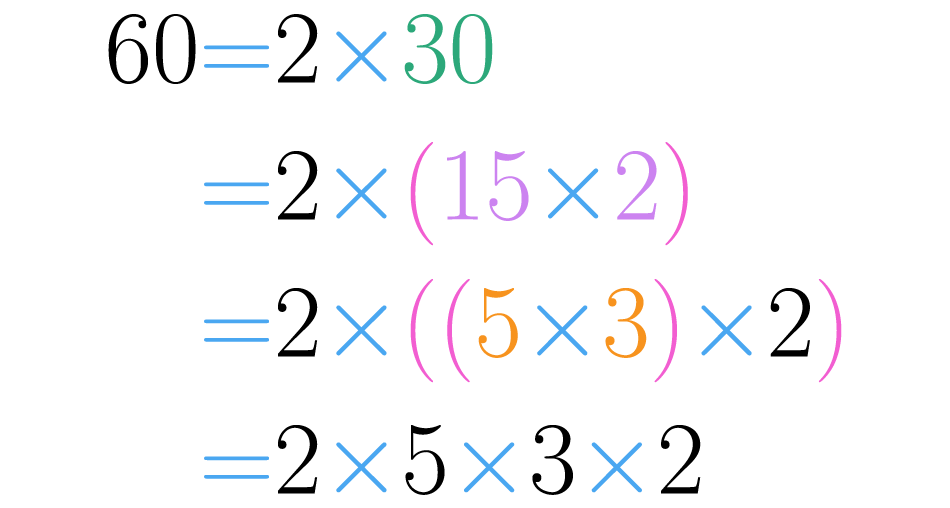
Lo anterior vale para todos los números, y significa que todo número natural mayor que uno, o es primo, o se puede escribir como producto de primos. Esta afirmación es una de las más importantes de la matemática, y como tal recibe un nombre especial: teorema fundamental de la aritmética.
A la hora de descomponer números en factores primos se pueden encontrar algunos con una gran cantidad de factores. Un ejemplo de ello es :
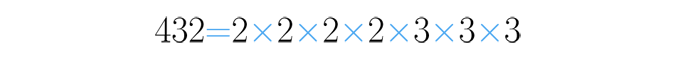
Para simplificar la escritura de estas descomposiciones se hace lo siguiente: solo anotamos una vez cada factor primo, pero escribimos las veces que se repite con un pequeño número arriba al lado derecho.
Así, la descomposición de se expresa: , ya que el factor dos aparece cuatro veces y el factor tres aparece tres. Leemos este tipo de expresiones así: “dos a la cuatro, por tres a la tres”.
En la expresión se conoce a como exponente, mientras que es llamado base. En la expresión , es el exponente y es la base. A esta forma de escribir los productos se le conoce como potenciación.
/es/divisores-y-multiplos/descomposicion-en-numeros-primos/content/