Aplicaciones de la matemática
Tamaño del sistema solar


/es/aplicaciones-de-la-matematica/la-marea/content/
Si el sol fuera del tamaño de una pelota de básquetbol, la tierra sería del tamaño de una pulga, y estaría orbitando alrededor de la pelota a una distancia de metros. La luna sería del tamaño de un grano de arena y daría vueltas a la pulga a una distancia de cm.
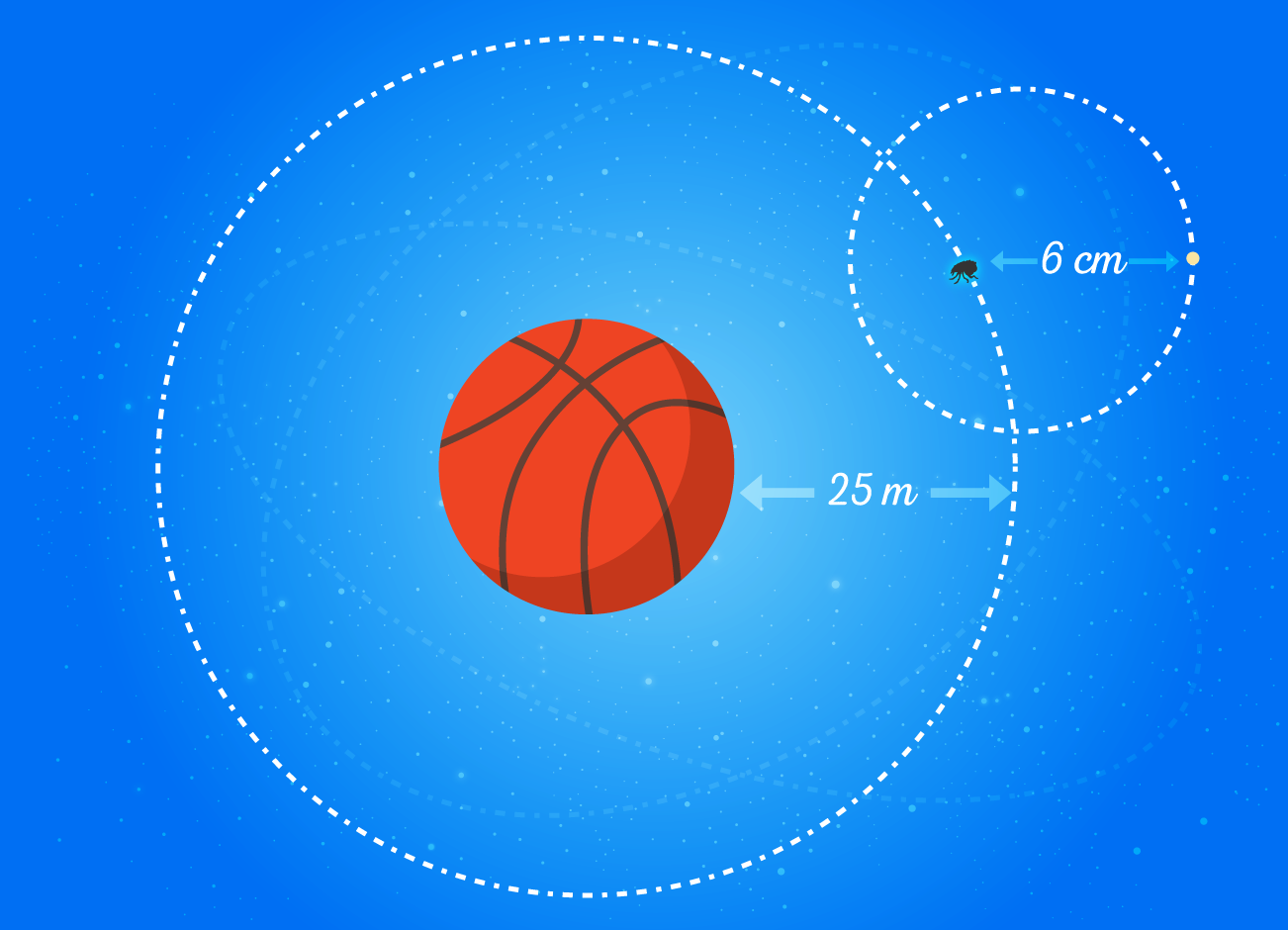
He llegado a estas conclusiones gracias al concepto de proporción, con él podemos hacer más comparaciones curiosas para entender nuestro hermoso sistema solar. Para seguir, primero entendamos qué son las proporciones.
En matemáticas, una razón es una relación entre dos cantidades. Para calcularla, debemos realizar la división entre las mismas. Por ejemplo, para calcular la razón entre los números y , debemos realizar la división :
Como el resultado de la división es , decimos que la razón entre y es .
Para hacer las analogías descritas al principio, se eligió un objeto para comparar con el tamaño del sol, en este caso, una pelota de básquetbol que mide centímetros. Luego se calculó la razón entre el tamaño real, , y el tamaño ficticio, eso sí, teniendo en cuenta que son kilómetros:
Esta razón nos permitirá calcular el tamaño de los demás cuerpos del sistema solar. Si queremos determinar el tamaño de otro objeto, tendremos que elegir el adecuado para que entre el tamaño real y el ficticio se tenga la misma razón que acabamos de obtener entre sol y la pelota. Veamos por ejemplo qué tamaño que debería tener Júpiter: sabemos el diámetro real de ese planeta: para conservar la razón, debemos encontrar un tamaño ficticio tal que:
Llamamos a la igualdad entre dos razones proporción. Para encontrar el número preciso solo debemos dividir el tamaño real en la razón:
De la última expresión encontramos que el tamaño ficticio de Júpiter debería ser . Esto quiere decir que si el sol fuera una pelota de básquetbol, Júpiter tendría el tamaño aproximado de una mora y giraría en torno a la pelota a una distancia de casi metros.

Siguiendo con las analogías, podemos decir que si el sol fuera una pelota de básquetbol, Mercurio tendría el grosor de una aguja de jeringa (casi ) y orbitaría a metros; Marte sería tan grande como la punta de un lápiz y estaría a casi metros de la pelota; Saturno, sin contar sus anillos, entraría justo por la boca de una botella de plástico ( aprox.) y estaría a unos metros del balón; Plutón, un poco más pequeño que un grano de sal , estaría a más de un kilómetro de la pelota. ¿Te imaginas? un granito de sal girando alrededor de una pelota de básquet, a más de un kilómetro de distancia.
Existe una región del sistema solar llamada Nube de Oort, de la que se cree provienen los cometas más lejanos. En la vida real esta región está ubicada a un año luz de nuestro sol, si aplicamos la proporción obtendremos que la Nube de Oort estaría a unos de la pelota. ¿No te parece increíble que un objeto de de diámetro, ejerza su influencia a través del espacio vacío hasta una distancia mayor que atravesar Francia y Alemania juntas? Esto es lo que hace el sol, su gran masa ejerce influencia sobre objetos que están a más de un año luz de distancia.
Y para terminar: ¿qué tan lejos de la pelota de básquetbol crees que estaría la estrella más cercana?... A , una distancia aproximada a la que hay entre el norte de Colombia y el sur de Argentina.
Como podrás ver, las proporciones han sido una gran herramienta para poder hacernos a una idea de lo que es nuestro sistema solar, y esta es solo una de sus aplicaciones. ¡Hasta la próxima!
/es/aplicaciones-de-la-matematica/los-numeros-binarios/content/