Aplicaciones de la matemática
La marea


/es/aplicaciones-de-la-matematica/fases-y-eclipses-de-la-luna/content/
En el anterior artículo dedicado a la luna, estudiamos el porqué de sus fases y de los eclipses. En esta ocasión estudiaremos cómo la luna provoca las mareas y porqué, desde la tierra, vemos solo una de sus caras.
Para entender las mareas, debes saber que la fuerza de gravedad es más fuerte en cuanto más cerca estén los cuerpos que se atraen; a mayor distancia, menor fuerza de gravedad.
Ahora imagina a la luna girando en torno a la tierra. De la misma forma que la tierra ejerce atracción sobre cada punto de la luna, la luna ejerce atracción sobre cada punto de la tierra. Sin embargo, hay unos puntos de la tierra más cerca de la luna, estos puntos son atraídos con mucha más fuerza que los que están más lejos.
En la siguiente figura se representan con flechas las fuerzas hechas por la luna en diferentes puntos de la tierra. Entre más grande es la fuerza, la flecha que la representa es más larga y gruesa.
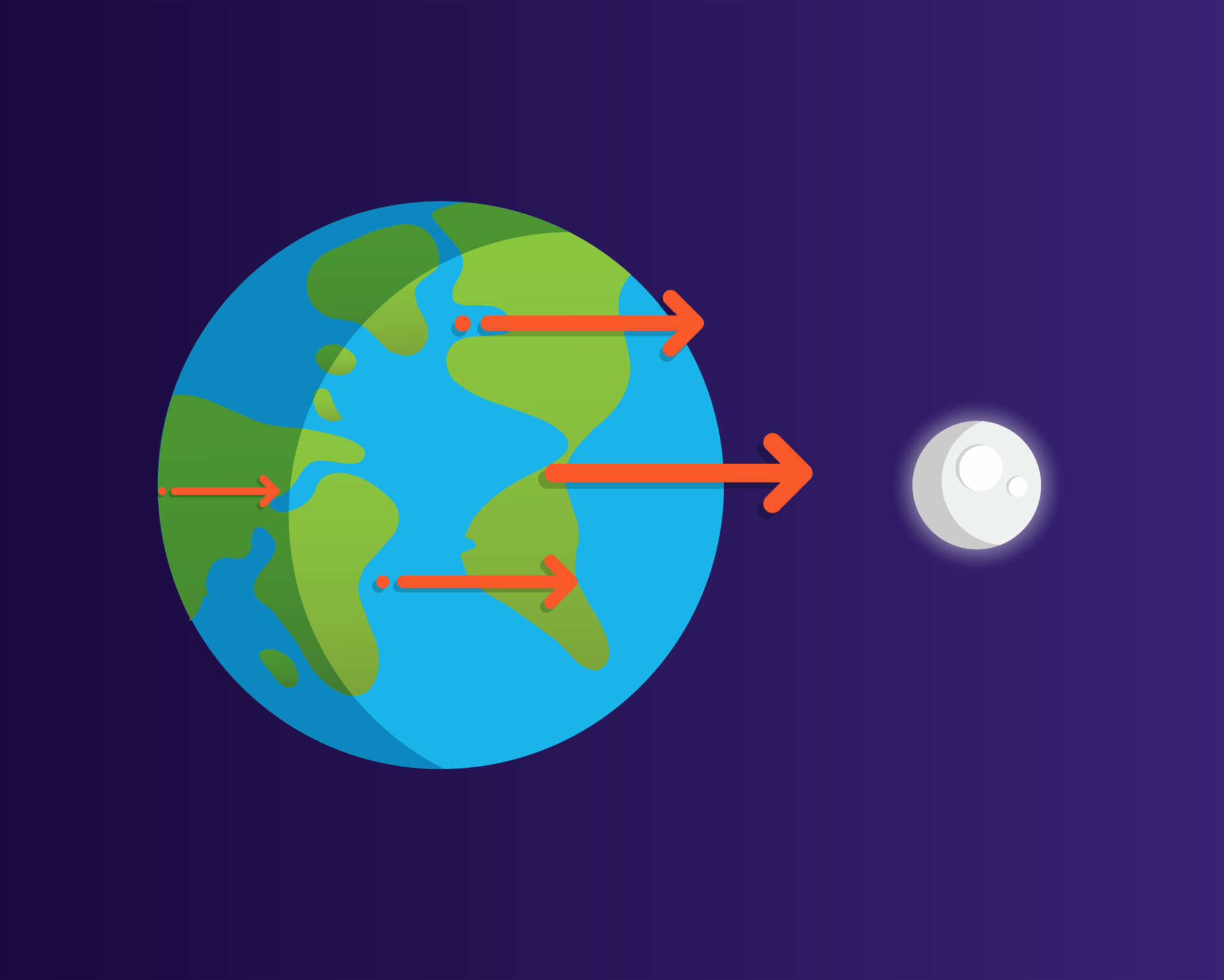
Observa que en los puntos más lejanos a la luna, su influencia es menor; mientras que en los más cercanos, la fuerza que se siente es mayor. Esta diferencia en la fuerza de atracción entre unos puntos y otros provoca una deformación, este fenómeno se conoce como efecto de marea.
Aunque te sea difícil de creer, la parte sólida de la tierra sufre una deformación que es conocida como marea terrestre. En algunos casos, como los equinoccios, la amplitud de esta deformación puede llegar hasta los 50 cm.
Gracias a la naturaleza misma del aire y el agua, la atmósfera y los mares son más susceptibles a estas deformaciones. En el caso de las mareas atmosféricas, la amplitud de la deformación puede llegar a kilómetros; mientras que la diferencia entre el nivel del mar, según sea la posición de la luna, puede llegar a ser de varios metros.
Como podrás imaginar, el sol también produce sobre la tierra un efecto de marea, pero debido a que está más lejos, su efecto es la mitad del ejercido por la luna. Sin embargo, cuando el sol y la luna están alineados sus efectos se suman, produciendo mareas mucho más grandes, estas son conocidas como mareas vivas. En cambio, cuando forman un ángulo de 90º con respecto a la tierra, sus efectos se neutralizan parcialmente produciendo mareas más pequeñas, estas son conocidas como mareas muertas. En el siguiente gráfico podrás apreciar estas situaciones:
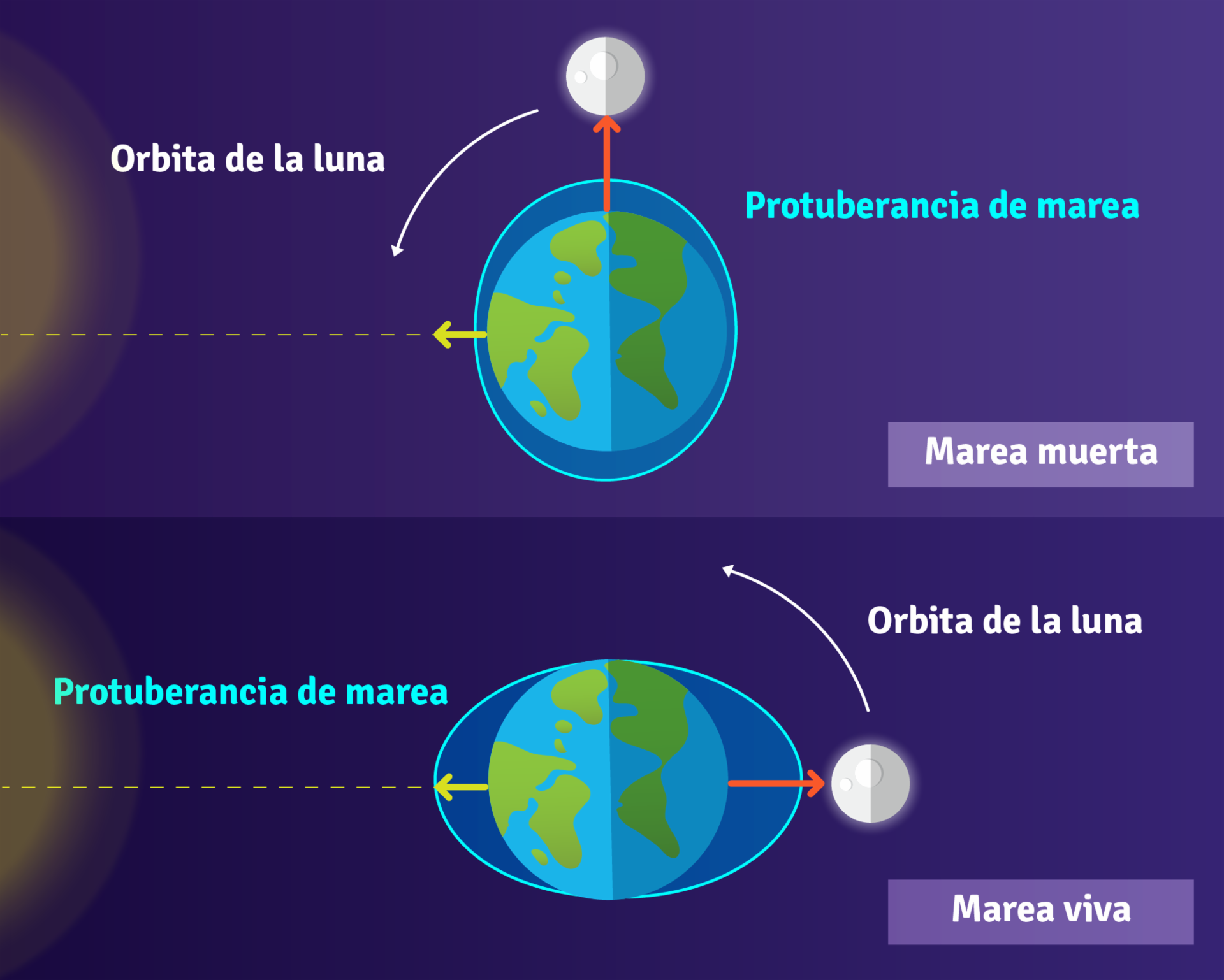
Las flechas amarilla y roja muestran la fuerza que actúa sobre el mar por efecto del sol y la luna respectivamente. La zona ovalada azul representa la suma de estos dos efectos sobre el mar.
La tierra también produce un efecto de marea sobre la luna. Debido a esto, al tener la luna mucha menos masa que la tierra, y a que la distancia entre las dos es relativamente poca, se produce un fenómeno conocido como acoplamiento de marea.
Como resultado, el tiempo de traslación de la luna alrededor de la tierra, y su rotación, se han vuelto iguales. Por esta razón podemos ver sólo uno de sus lados, observa lo que sucede al girar la luna, una vez entorno a sí misma, por cada vuelta que da a la tierra:
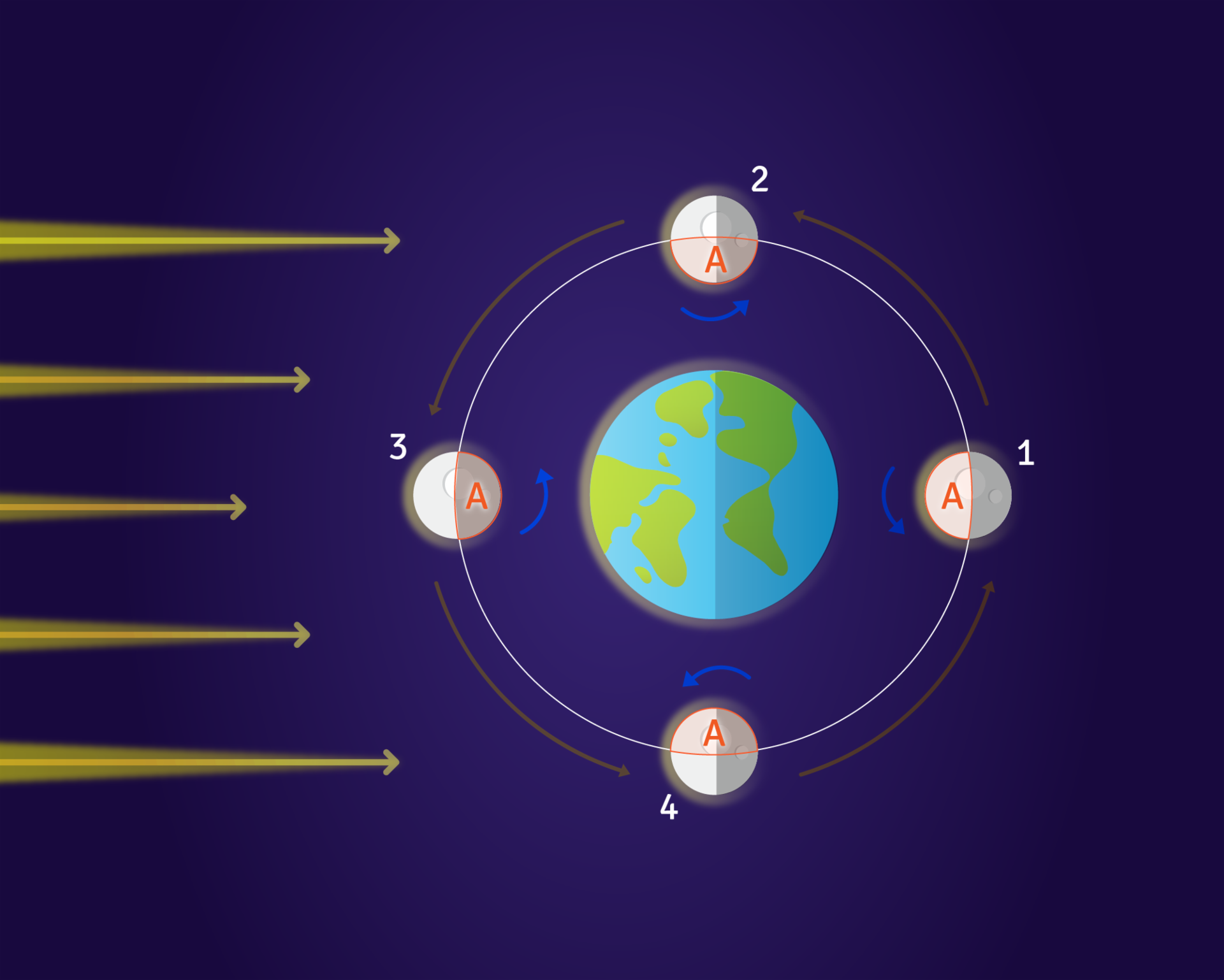
En la imagen anterior, se ha marcado una mitad de la luna con la letra A. Fíjate que en la posición 1, la letra A está orientada hacia la izquierda, en la posición 2 hacia abajo, en la posición 3 hacia la derecha, en la posición 4 hacia arriba y, de vuelta en la posición 1, otra vez hacia a la izquierda. En total ha dado una vuelta sobre sí misma, y una vuelta alrededor de la tierra. Sin embargo, desde la tierra, parece que no se moviera, ya que sólo podemos ver la mitad de la luna marcada con la letra A.
/es/aplicaciones-de-la-matematica/tamano-del-sistema-solar/content/