Percents -
Introduction to Percentages

Percents
Introduction to Percentages


A percentage is another way of writing a decimal. Just like decimals, a percentage is a part of a whole. Basically, it's less than 1 whole thing, but more than 0.
We use percentages all the time in real life. For example, have you ever left a fifteen percent tip at a restaurant? Or bought something on sale for twenty percent off? Those are both percentages—15 percent and 20 percent.
Click through the slideshow to learn how percentages work.
As you saw in the slideshow, every percentage has two parts: a number and the percent sign (%). When you write a percentage, you'll write the number first, then the percent sign. Let's try it! How would you write this percentage?
nine percent
First, we'll write the number, nine, and then the percent sign (%). So our percentage will look like this:
9%
Try writing the correct percentage in the box.






When you read a percentage out loud, you'll need to read two parts: the number and the percent sign (%). Let's look at an example:
25%
25% is twenty five out of one hundred. We'd read 25% like this:
twenty-five percent
Sometimes percentages might have a decimal. For example:
7.5%
Here, 7.5% means we have seven-and-a-half out of one hundred. We'd read it like this:
seven point five percent
OR
seven and a half percent
You can read any percentage with a decimal point like this. How about 10.25%? That's ten and one quarter out of one hundred, so we'd read it as ten point two five percent, or ten and a quarter percent.
Try reading each of the percentages below aloud.

Let's imagine you're shopping for apple juice. You find two different kinds—one contains 20% real juice, while the other contains 50% real juice.

Do you know which bottle has more real juice? Since both bottles are the same size, we can simply compare the numbers to see which percentage is larger.

50 is larger than 20, so 50% is a larger percentage than 20%. The larger the number next to the percent sign, the larger the percentage.
What about these percentages?
7% and 17%
Which is larger? Again, we'll look to see which number is larger. 17 is larger than 7, so 17% is a larger percentage than 7%.
What if you had to compare two percentages like this?
5.4% and 5.5%
At first glance, it might be difficult to tell which percentage is larger. Remember, this is just another way of asking, "Which is larger, five and four-tenths of a percent or five and five-tenths of a percent?" Since the first number is the same for both fractions, we'll compare the numbers to the right of the decimal place.
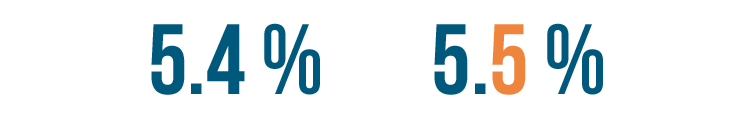
5 is larger than 4, so 5.5% is larger than 5.4%.
What about these percentages?
5.55% and 5.56%
Again, since the first number is the same, we'll compare the numbers to the right of the decimal place.

56 is larger than 55, so 5.56% is larger than 5.55%.
/en/percents/calculating-percentages/content/