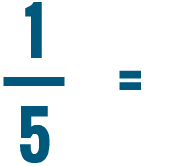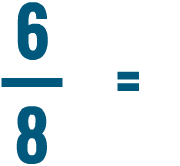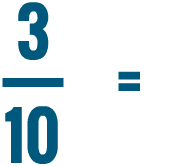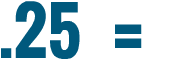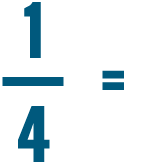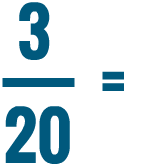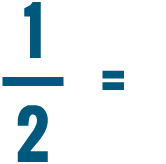/en/fractions/multiplying-and-dividing-fractions/content/
When we talk, we often use different words to express the same thing. For example, we could describe the same car as tiny or little or small. All of these words mean the car is not big. Fractions, decimals, and percents are like the words tiny, little, and small. They're all just different ways of expressing parts of a whole.
In this image, each measuring cup has the same amount of juice in it. But we've expressed this amount in three ways: as a fraction, as a percent, and as a decimal. Since they're expressing the same amount, we know that 1/2, 50%, and 0.5 are equal to each other. Any time we see 1/2, we'll know it can also mean 50% or 0.5.
Sometimes it's useful to convert one kind of number into another. For example, it's much easier to add 1/4 and 0.5 if you turn 0.5 into a fraction. Learning how to convert fractions, decimals, and percents will also help you as you learn more advanced math.
Every fraction can also be written as a decimal, and vice versa. You may not do this very often, but converting decimals and fractions can help you in math. For example, it's easier to subtract 1/6 from 0.52 if you turn 1/6 into a decimal first.
Let's convert a fraction into a decimal. We'll be using a math skill you've already learned: long division. To refresh your memory on this skill, you can review our Long Division lesson.
Click through the slideshow to learn how to convert a fraction into a decimal.
Let's see how we can convert 1/4 into a decimal.
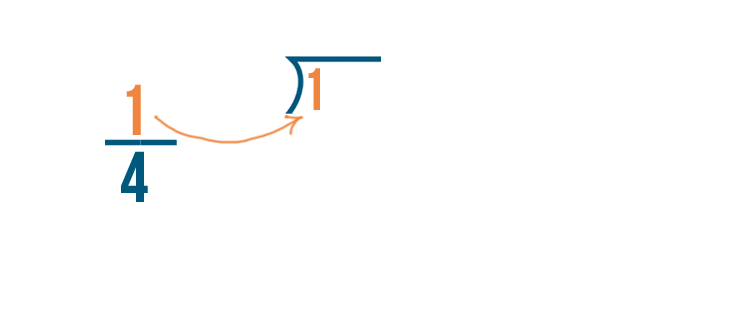
To convert a fraction into a decimal, we'll just divide the numerator...
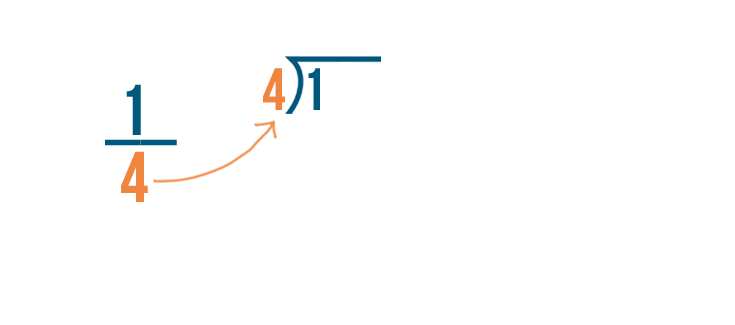
To convert a fraction to a decimal, we'll just divide the numerator...by the denominator.
In our example, we'll divide 1 by 4.
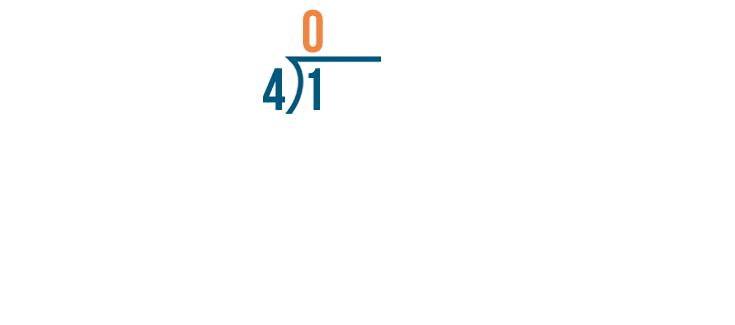
1 divided by 4 equals 0.
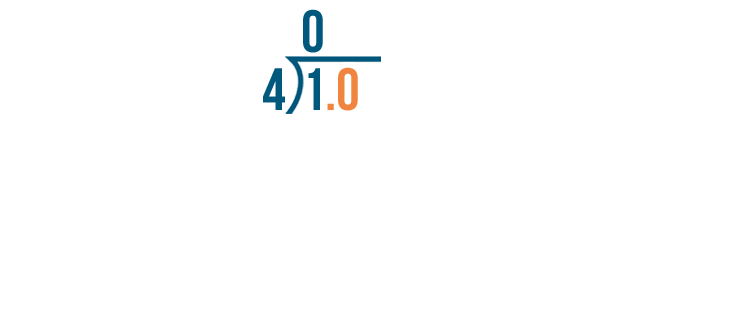
To keep dividing, we'll add a decimal point and a zero after the 1.
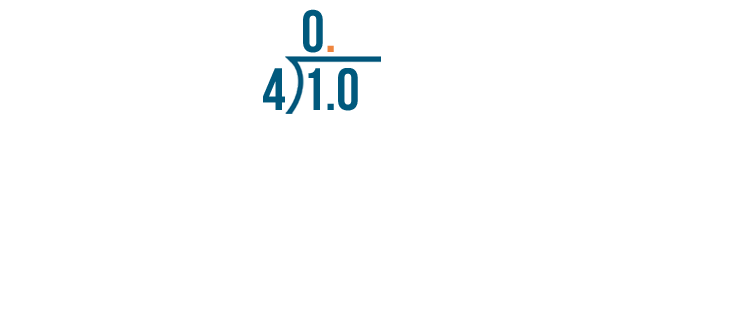
We'll also add a decimal point after the 0 on top.
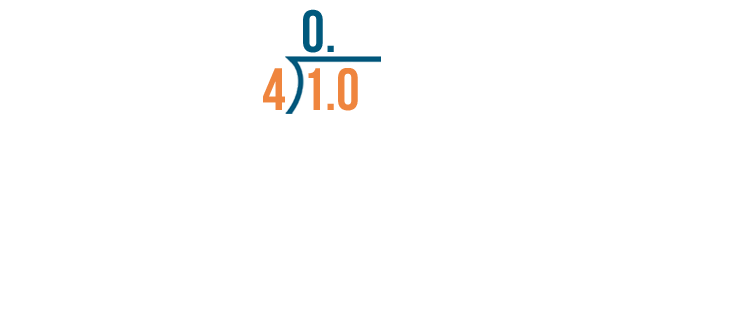
Now we can divide 10 by 4.
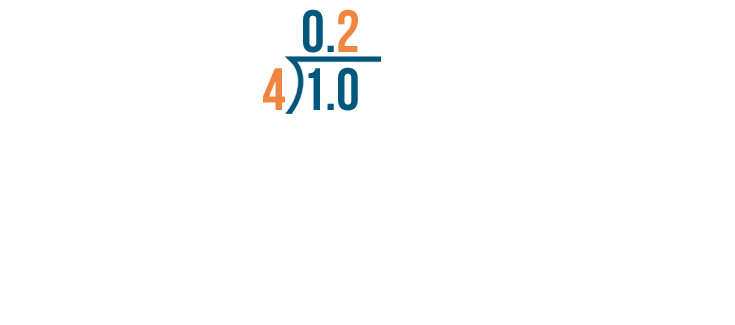
10 divided by 4 equals 2.
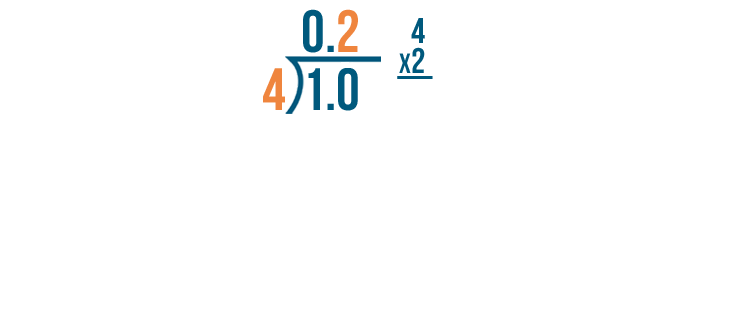
Now we'll multiply 4 by 2.
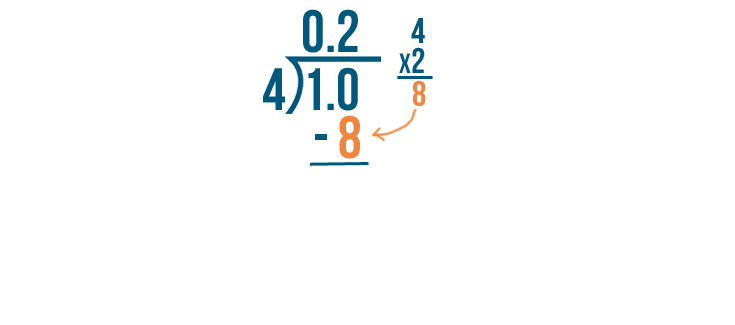
4 times 2 equals 8. So we'll subtract 8 from 10.
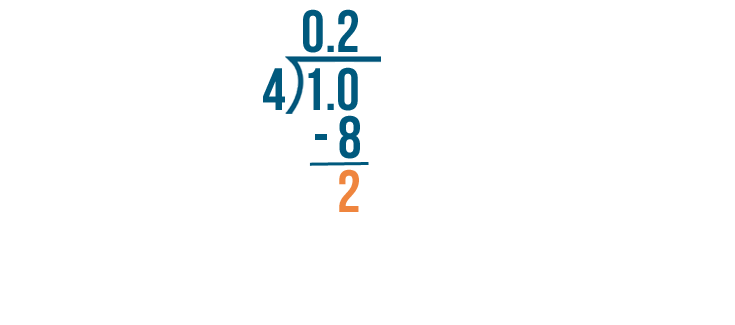
10 minus 8 equals 2.
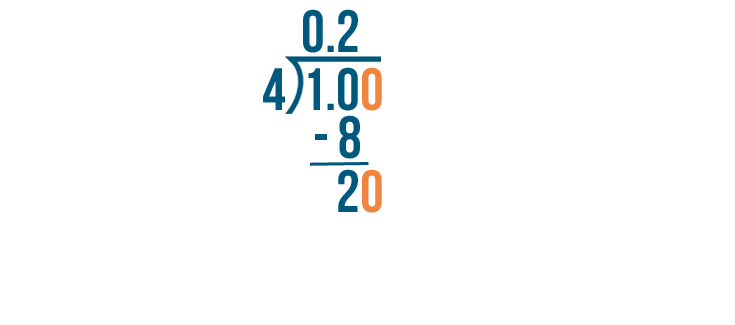
Since 2 is greater than 0, we're not finished dividing yet. We'll add another 0 after the decimal point and bring it down.
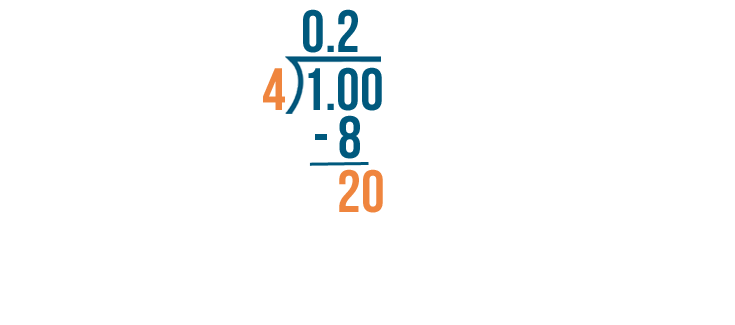
Now we'll divide 20 by 4.
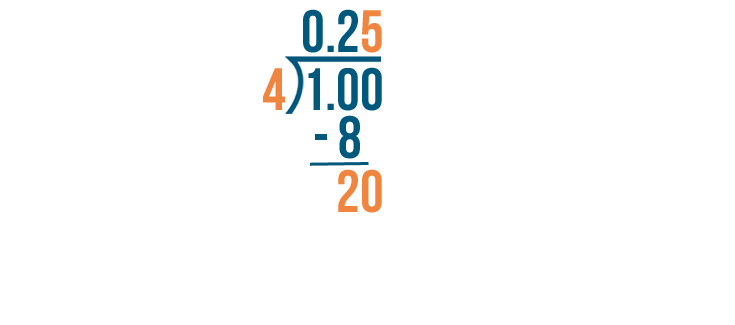
20 divided by 4 equals 5.
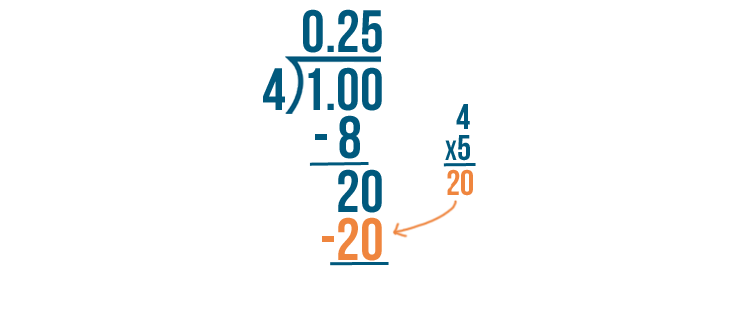
Now we'll multiply. 4 times 5 equals 20.
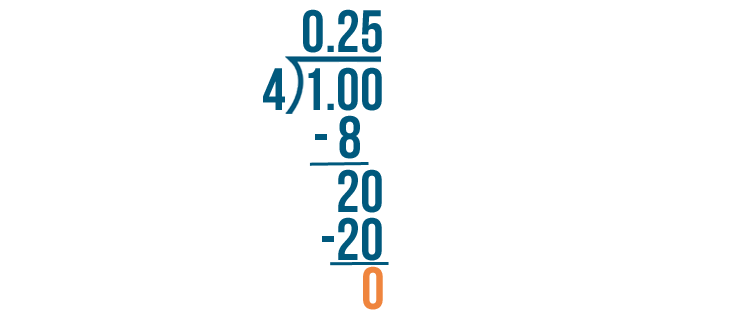
When we subtract 20 from 20, we get 0. The 0 means we're done dividing.
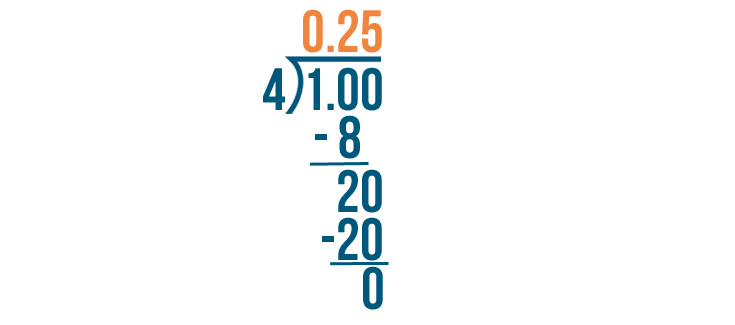
1 divided by 4 equals 0.25.
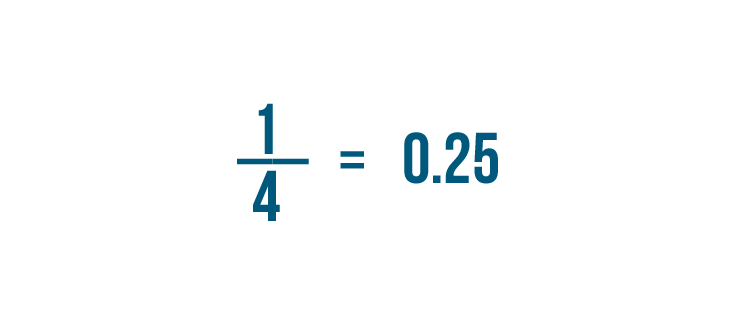
So 1/4 is equal to 0.25.
Convert each of these fractions into a decimal.
Now we'll do it in reverse. Let's convert a decimal into a fraction.
Click through the slideshow to see how to convert a decimal into a fraction.
We're going to rewrite 0.85 as a fraction. To convert a decimal into a fraction, we'll use place values.
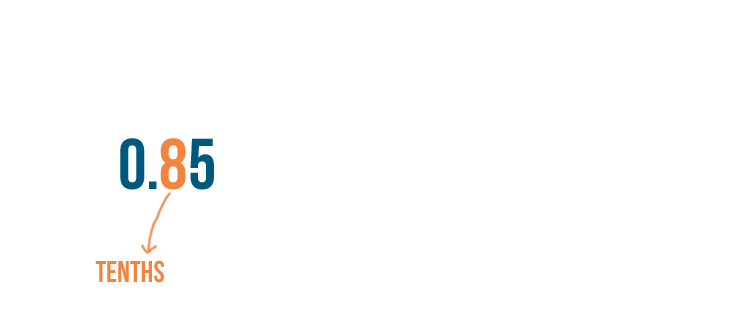
In decimals, the number immediately to the right of the decimal point is in the tenths place.
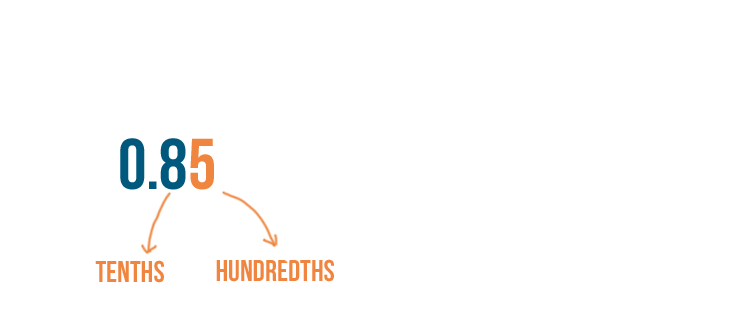
The place to the right of the tenths place is the hundredths place.
To convert a decimal, first we'll check the place value of the last number to the right.
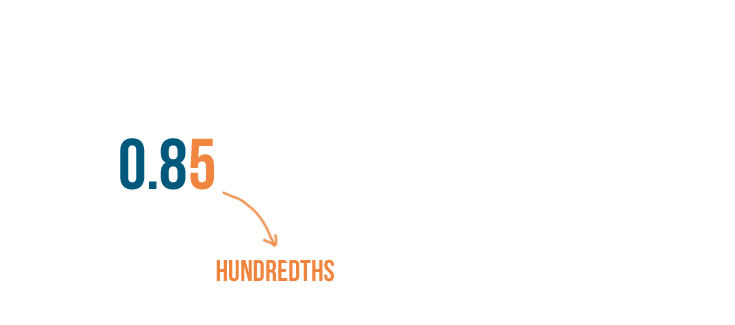
In 0.85, 5 is in the hundredths place.
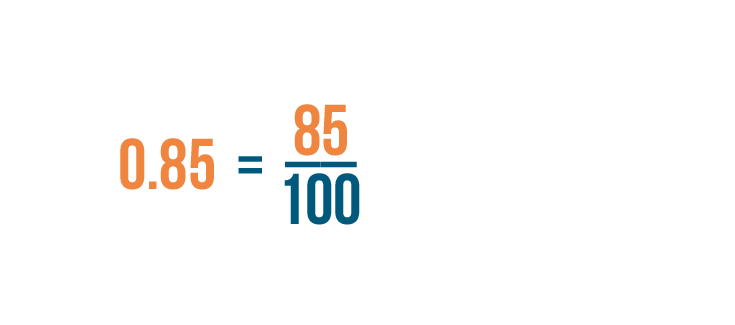
This means our decimal is equal to 85 hundredths. 85 hundredths can also be written as 85/100.
Now we have our fraction. But it's always a good idea to reduce fractions when we can—it makes them easier to read.
To reduce, we need to find the largest number that will go evenly into both 85 and 100.
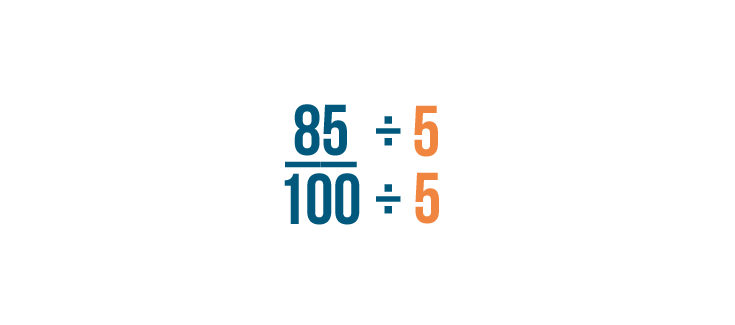
5 is the largest number that goes evenly into 85 and 100. So we'll divide both parts of our fraction by 5.
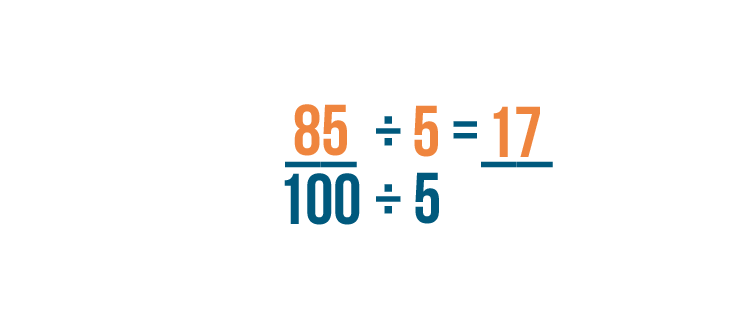
First we'll divide the numerator. 85 divided by 5 equals 17.
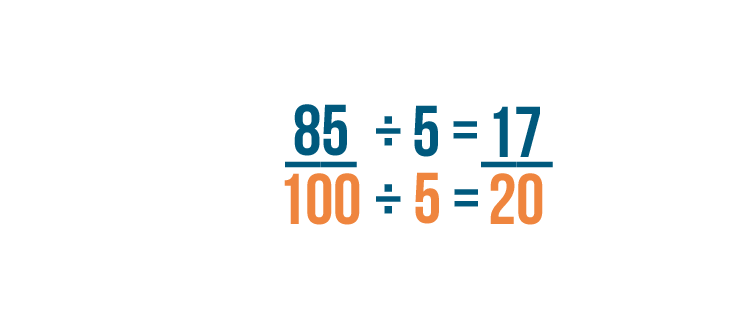
Now we'll divide the denominator. 100 divided by 5 equals 20. This means 85/100 can be reduced to 17/20.
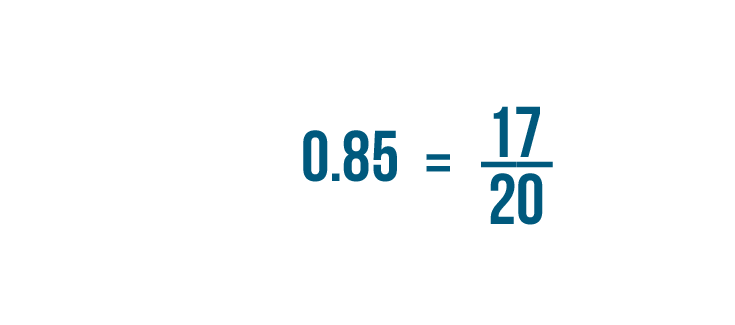
So 0.85 is equal to 17/20.
Reducing a fraction may seem unnecessary when you're converting a decimal. But it's important if you're going to use the fraction in a math problem. If you're adding two fractions, you may even need to reduce or change both fractions so they have a common denominator.
Convert these decimals into fractions. Be sure to reduce each fraction to its simplest form!
Knowing how to convert percents and decimals will help you calculate things like sales tax and discounts. To learn how, check out our Percentages in Real Life lesson.
Converting a percent into a decimal is surprisingly easy. It only takes a few simple steps.
Click through the slideshow to learn how to convert a percent into a decimal.
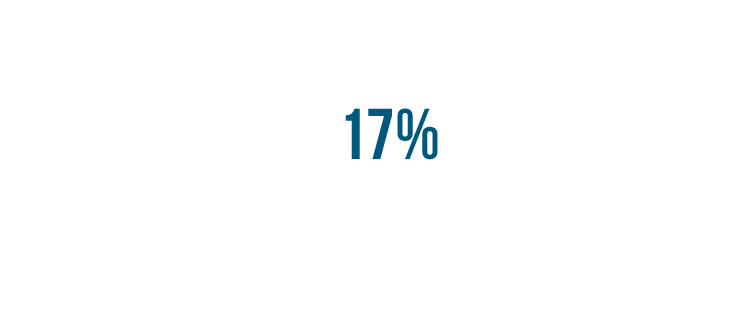
We're going to convert 17% into a decimal.
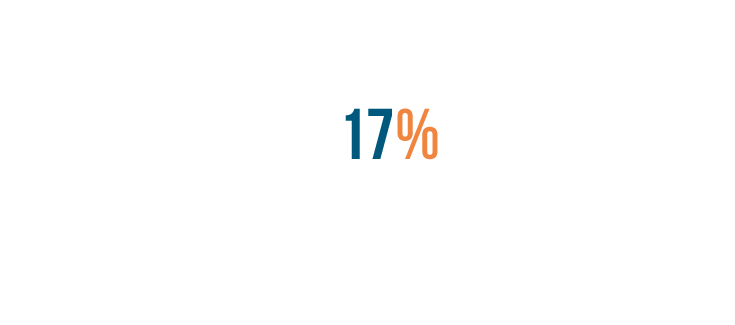
First, we'll take the percent sign...
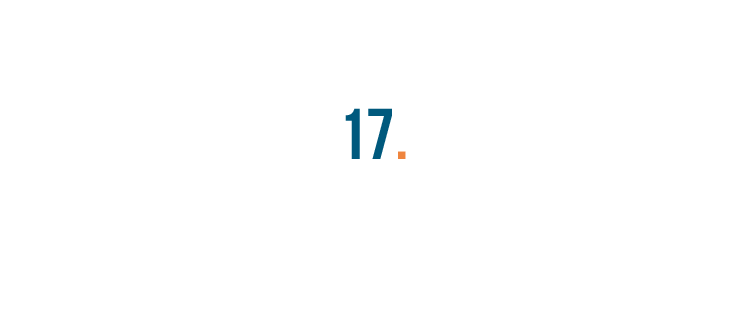
First, we'll take the percent sign...and turn it into a decimal point.
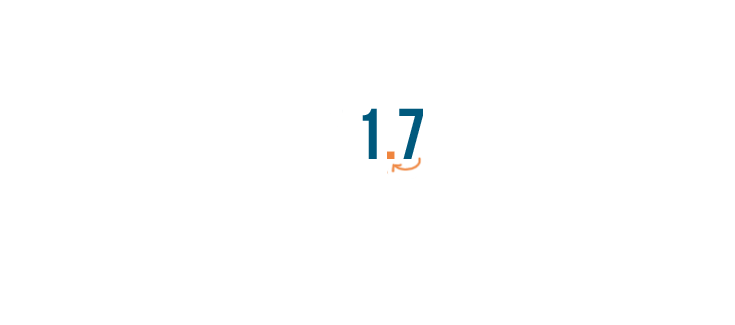
Next, we'll move the decimal point two spaces to the left.
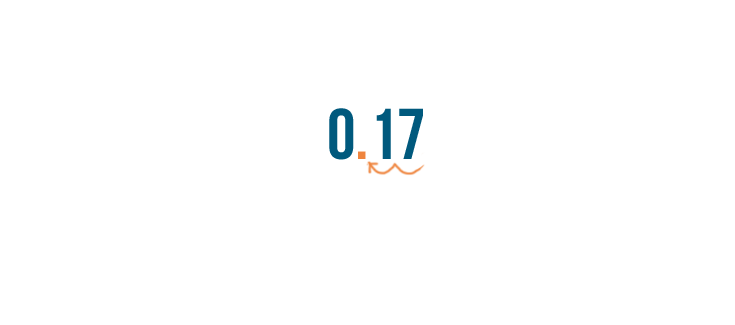
Now we'll move the decimal point two spaces to the left.
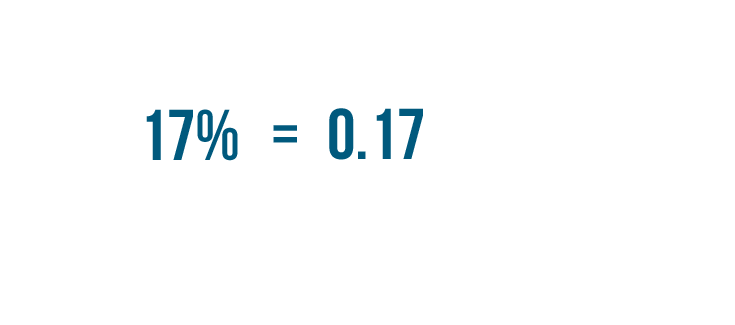
We've converted our percent to a decimal. 17% is equal to 0.17.
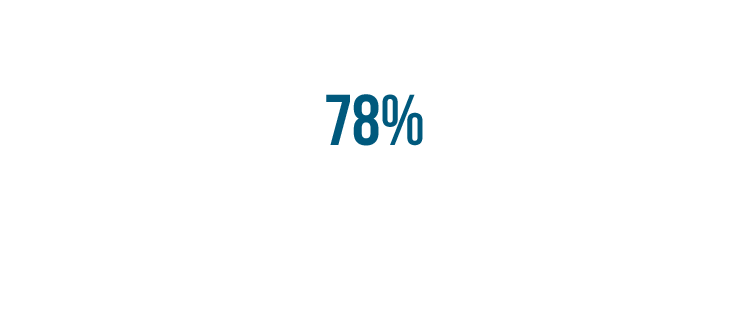
Let's look at another example. This time we'll turn 78% into a decimal.
First, we'll replace the percent sign with a decimal point.
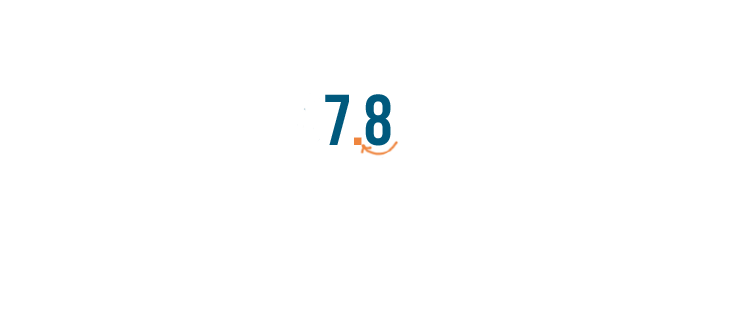
Then we'll move the decimal point two spaces to the left.
Then we'll move the decimal point two spaces to the left.
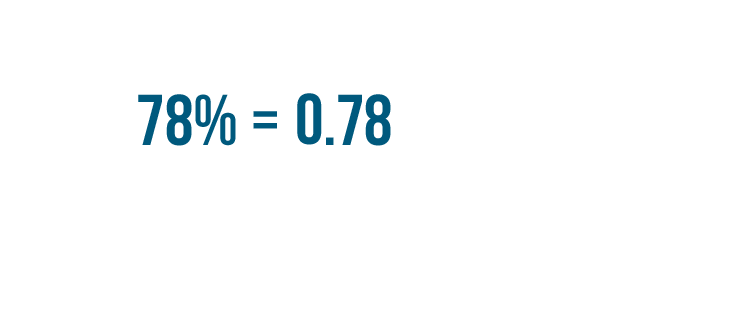
78% is equal to 0.78.
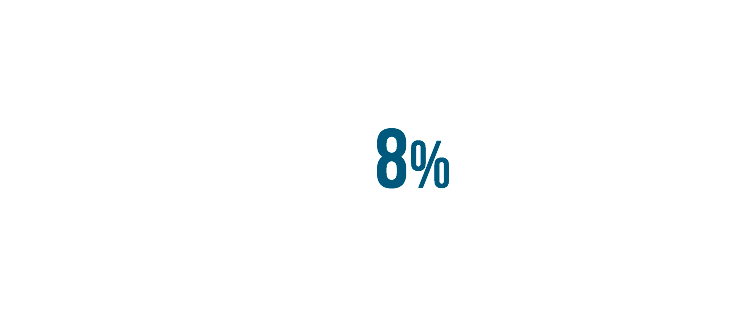
Let's look at another example. This time we'll turn 8% into a decimal.
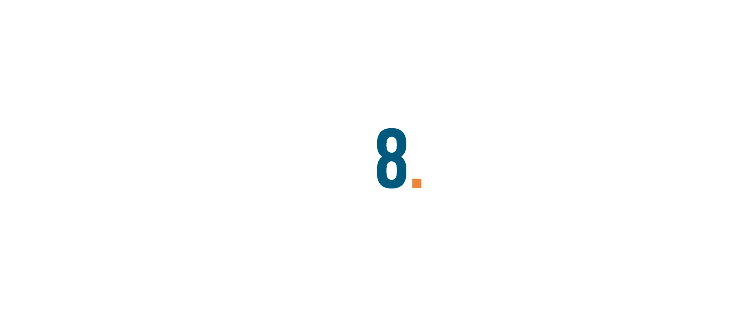
First, we'll replace the percent sign with a decimal point.
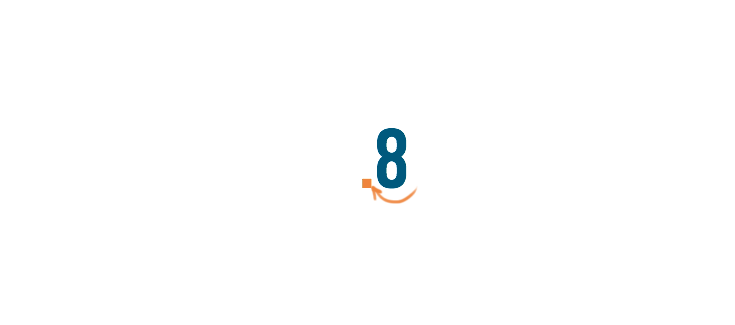
Then, we'll move the decimal point two spaces to the left.
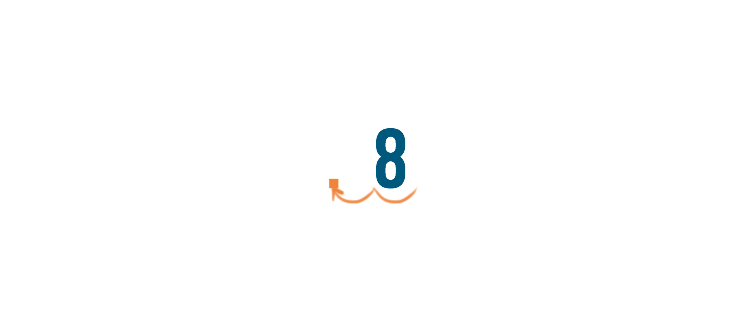
Then, we'll move the decimal point two spaces to the left.
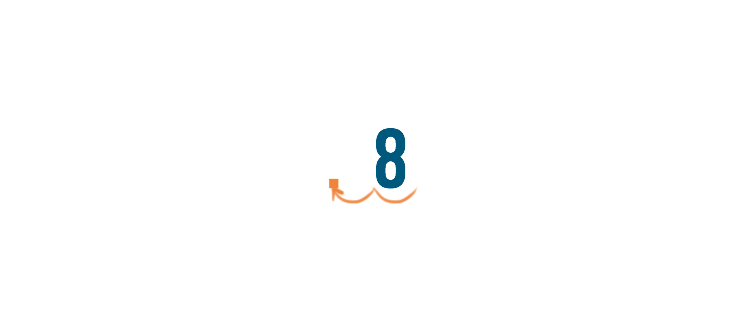
Notice there is an extra space next to the 8. We can't just leave an open space with nothing in it. Since zero equals nothing, we'll replace the space with zero.
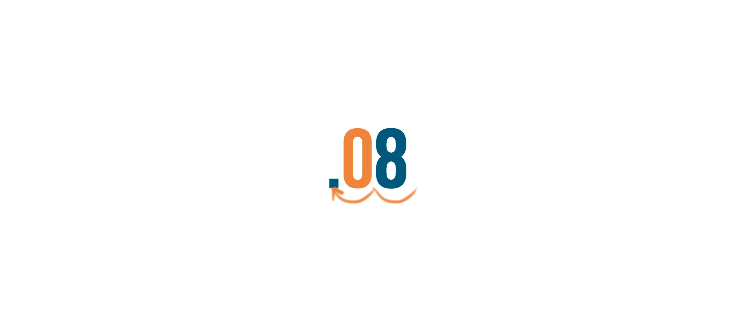
Notice there is an extra space next to the 8. We can't just leave an open space with nothing in it. Since zero equals nothing, we'll replace the space with zero.
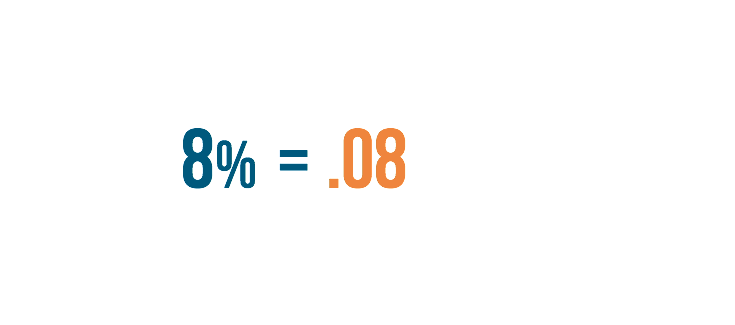
8% is equal to .08
Converting percents into decimals is so easy that you may feel like you've missed something. But don't worry—it really is that simple! Here's why the method we showed you works.
When we turn a percent into a decimal, we're actually doing two steps. First, we convert our percent into a fraction. Since all percents are out of 100, we just put the percent over 100, like this:
78% = 78/100
In the second step, we convert 78/100 into a decimal. You already know this means we'll divide the numerator by the denominator, like this:
78 ÷ 100 = 0.78
So why didn't we show you these steps in the slideshow? Because you can get the answer without them. You know that all percents are out of 100, so you can skip making the percent into a fraction. You have to divide the percent by 100 to get a decimal, but there's a quick way to do that. Just move the decimal point two spaces to the left! This way, you can get the same answer with just one easy step.
Convert these percents into decimals.
Now we'll reverse what you just learned. Let's convert a decimal into a percent.
Click through the slideshow to see how to convert a decimal into a percent.
We're going to convert 0.45 into a percent.
We'll reverse what we did in the last section. This time, we'll move the decimal point two places to the right.
We'll reverse what we did in the last section. This time, we'll move the decimal point two places to the right.
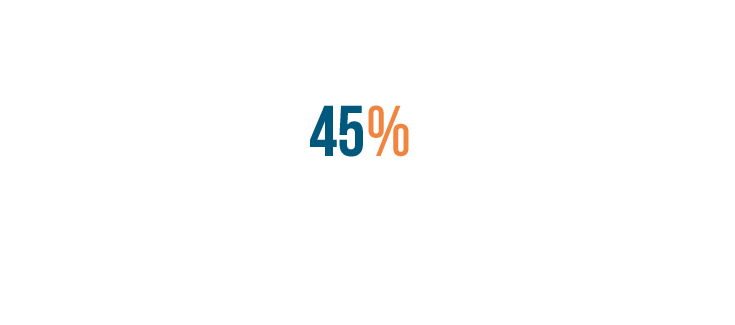
Now we'll replace the decimal point with a percent sign.
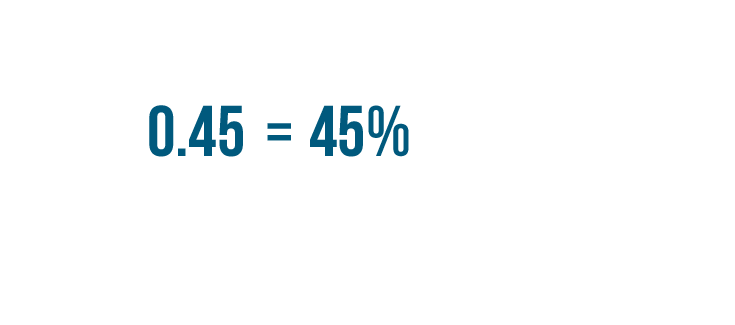
We've finished converting our decimal into a percent. 0.45 is equal to 45%.
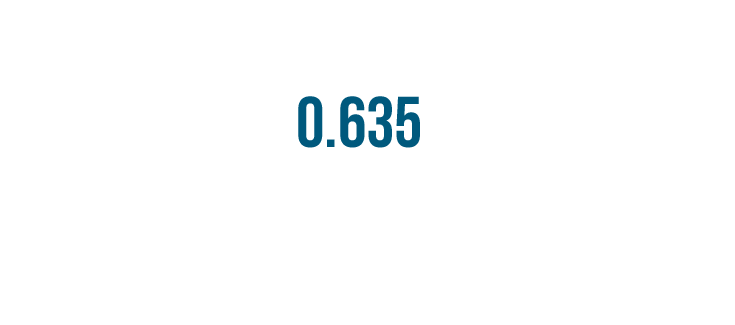
Let's try another example. This time our decimal has three numbers to the right of the decimal point.
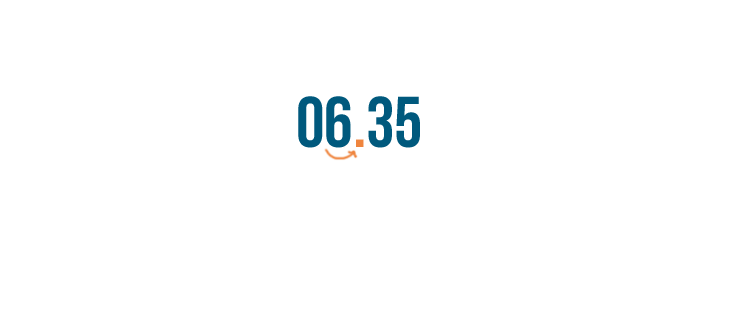
But we're still going to move the decimal point two spaces to the right.
But we're still going to move the decimal point two spaces to the right.
We still have a number to the right of the decimal point. The number isn't a 0, so we can't drop it.
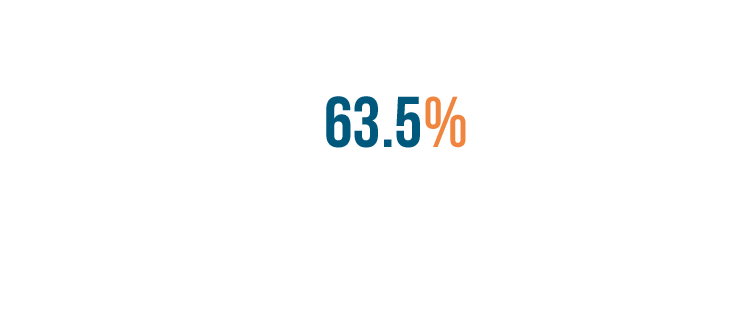
Instead, we'll keep the decimal point and add a percent sign at the end of the number.
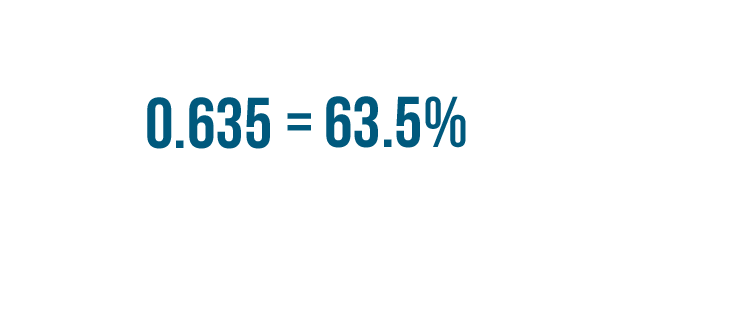
So 0.635 is equal to 63.5%.
Calculate these decimals as percents.
Knowing how to write percents as fractions and vice versa can help you in your everyday life. For example, let's say you earned a grade of 80% on a test. You can convert 80% into a fraction to find out how many of your answers were correct. When your teacher grades the test, she may do the opposite. If a student got 8 out of 10 questions right, the teacher can convert 8/10 to a percent to give the student a grade.
When you're converting a percent into a fraction, it helps to remember that percents are always out of 100. You can practice with percents in our Introduction to Percentages lesson.
Click through the slideshow to learn how to convert a percent into a fraction.
We're going to convert 30% into a fraction.
In Introduction to Percents, you learned that all percents are out of 100. In fact, that's what the word percent means.
So any percent is equal to itself over 100. In our example, 30% is equal to 30/100.
Now we've converted 30% into a fraction, but we still need to reduce it.
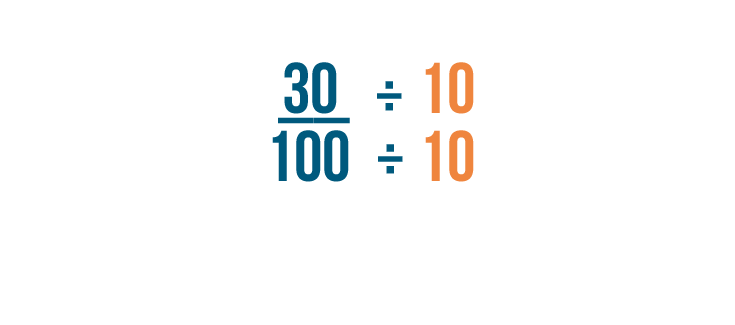
10 is the largest number that goes evenly into 30 and 100. So we can divide both parts of the fraction by 10.
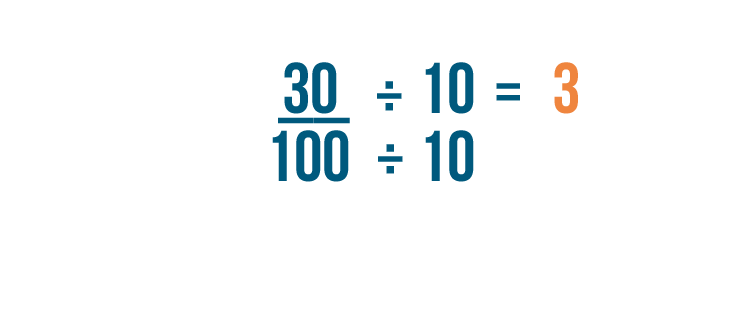
We'll divide the numerator of the fraction first. 30 divided by 10 equals 3.
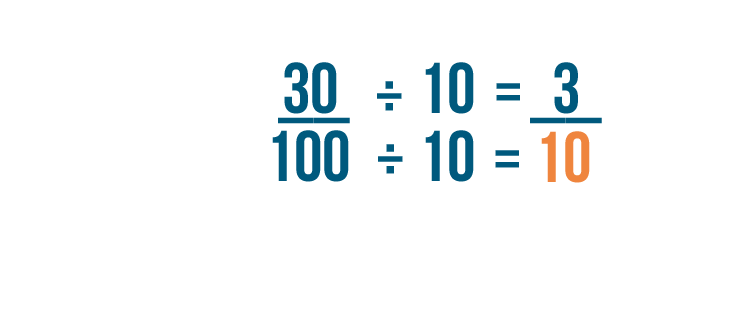
Now we'll divide the denominator. 100 divided by 10 equals 10.
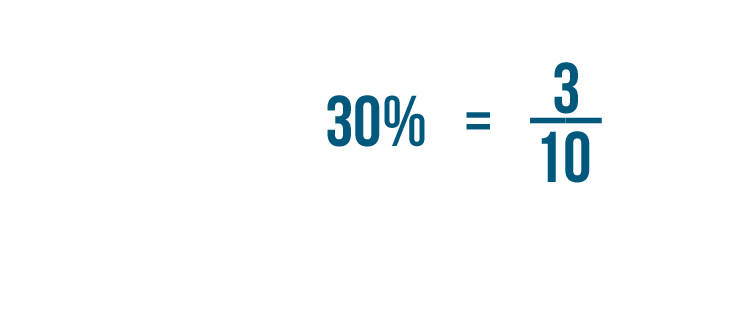
So 30% is equal to 3/10.
Write these percentages as fractions. Make sure to reduce each fraction to its simplest form.
Converting a fraction uses two of the skills you just learned: writing a fraction as a decimal, and writing a decimal as a percent. Let's see how we can use these skills to convert a fraction into a percent.
Click through the slideshow to learn how to convert a fraction into a percent.
Let's convert 3/6 into a percent.
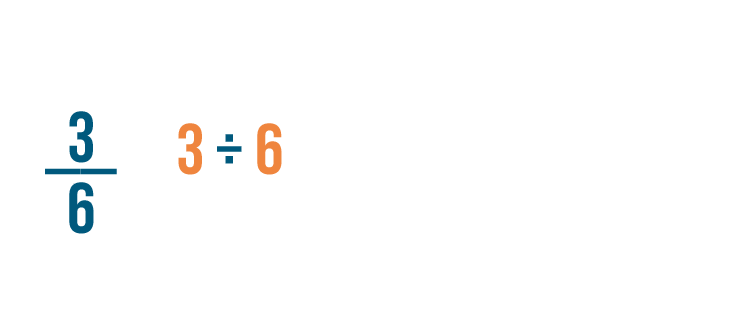
Just like when we converted a fraction into a decimal, we'll divide the numerator by the denominator.
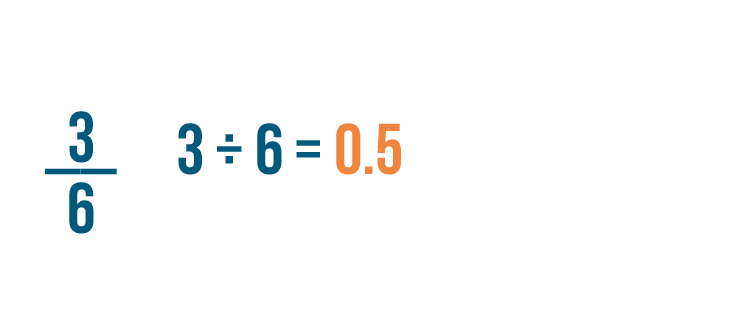
3 divided by 6 equals 0.5.
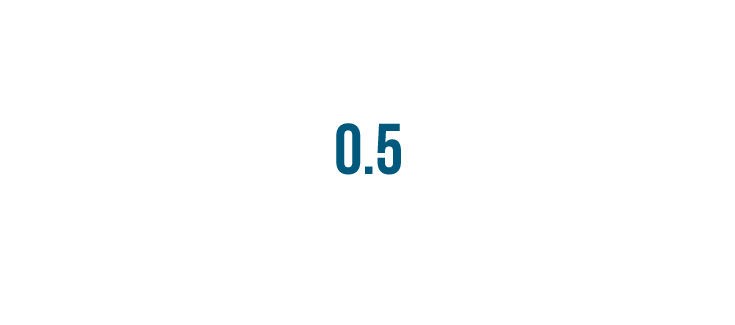
We've turned our fraction into a decimal.
Now we'll turn the decimal into a percent by moving the decimal point two spaces to the right.
Now we'll turn the decimal into a percent by moving the decimal point two spaces to the right.
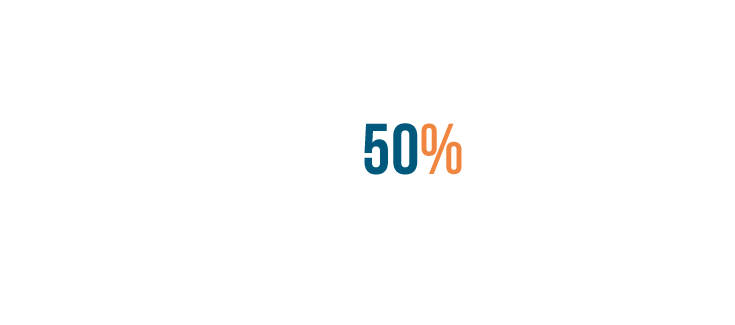
We'll also change the decimal point into a percent sign. 0.50 is equal to 50%.
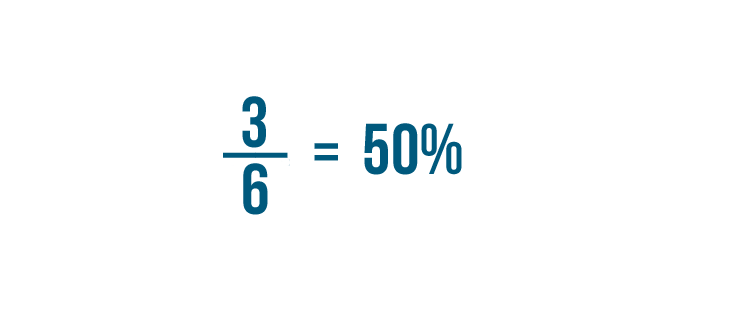
So 3/6 is equal to 50%.
Convert these fractions into percents.
