Lesson 3: Multiplying and Dividing Decimals
/en/decimals/adding-and-subtracting-decimals/content/
Multiplying with decimals
In Adding and Subtracting Decimals, you learned how to add decimal numbers. You may be able to think of times when you'd add decimals in real life. For example, let's say you go to the store and find a shirt you really like. The price tag says it costs $15.60. You like the shirt so much that you decide to buy five of them.
To figure out the total cost, you could add the prices.
Adding this many numbers could take a long time. In the lesson on multiplication, we learned that when you multiply, you are increasing a number many times. Because all of the shirt prices are the same, multiplication could help you solve this problem a little faster.
When you multiply decimal numbers, it's helpful to set up the problem in a way that makes it easier for you to solve it one step at a time.
Click through the slideshow below to learn how to set up a multiplication problem with decimals.

Instead of adding $15.60 + $15.60 + $15.60 + $15.60 + $15.60...
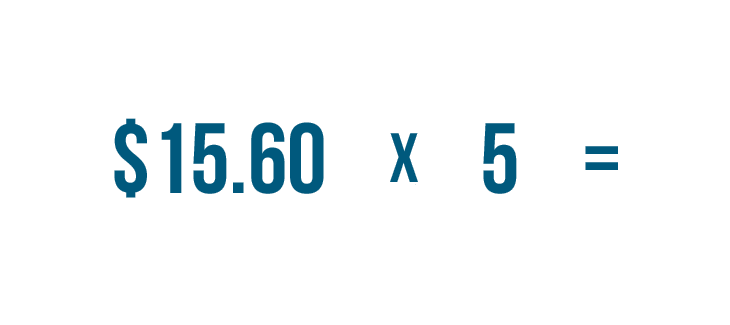
Instead of adding $15.60 + $15.60 + $15.60 + $15.60 + $15.60...we'll multiply $15.60 by 5.
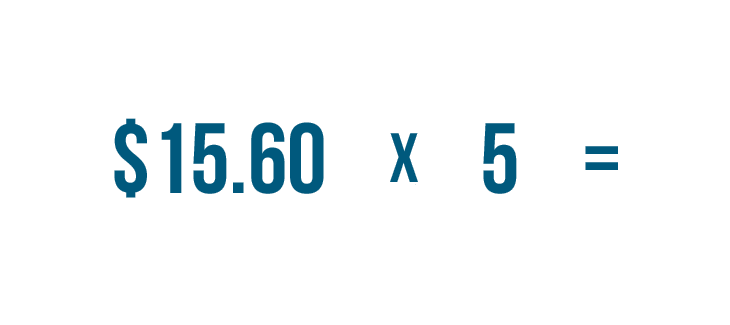
Let's set up our multiplication expression: $15.60 x 5. We'll stack the numbers one on top of the other.
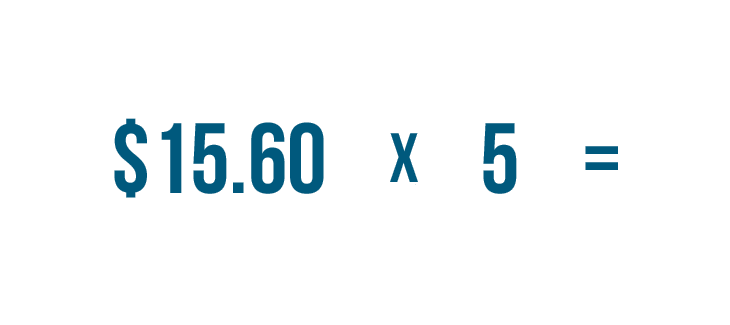
It's a good habit to place the number that has the most digits on top. This makes the problem easier to solve.
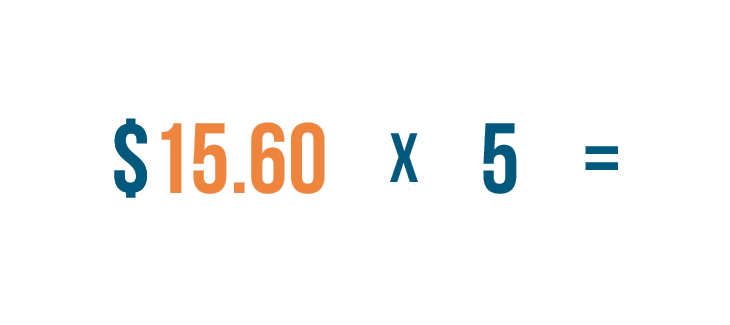
Let's look at the number of digits in each number. 15.60 has four digits...
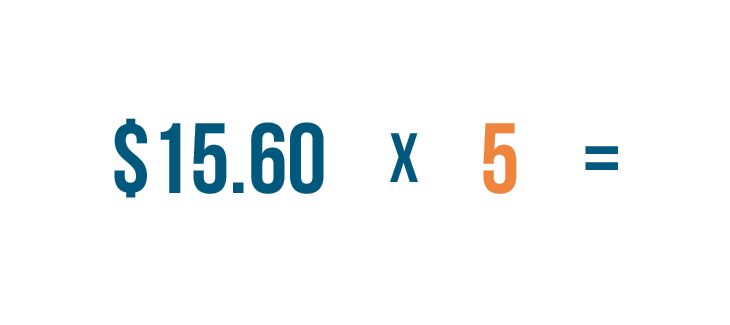
Let's look at the number of digits in each number. 15.60 has four digits...and 5 is one digit.
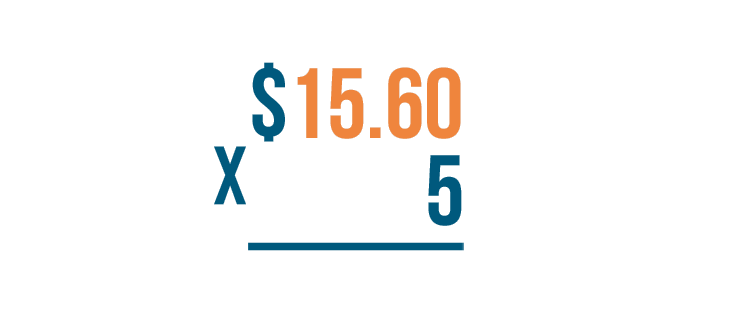
15.60 has more digits. This means we'll write 15.60 above the 5.
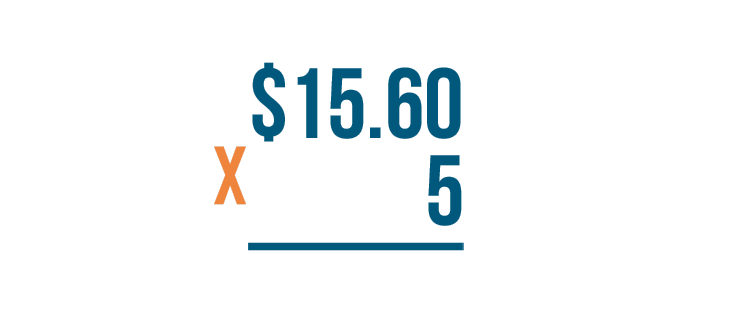
Since we're multiplying this number, we'll write the times sign (X) to the left of the numbers.
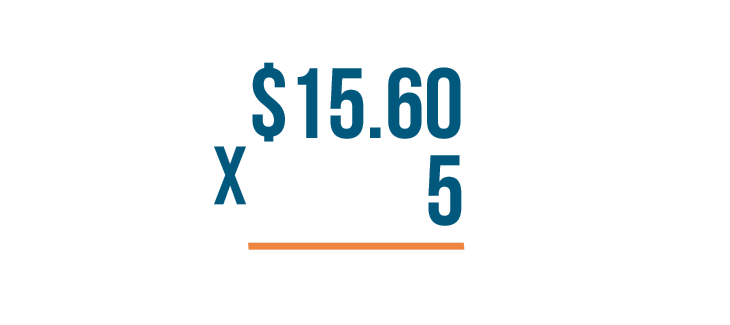
Instead of an equals sign (=), we'll put a line underneath the number on bottom.
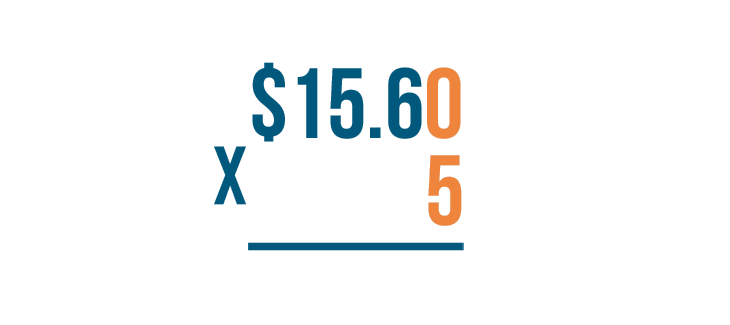
When writing a stacked multiplication expression with decimal numbers, the numbers should be lined up on the right.
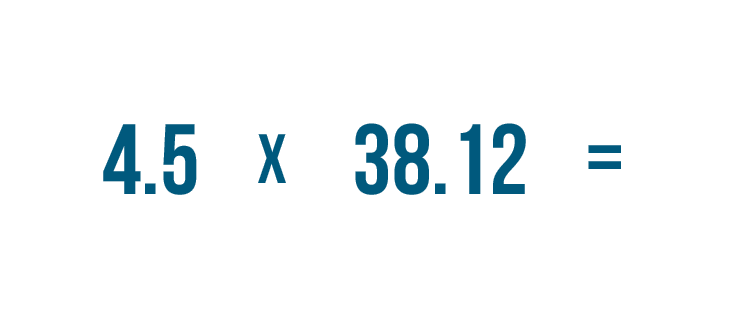
Let's look at another example. We'll stack this expression: 4.5 x 38.12.
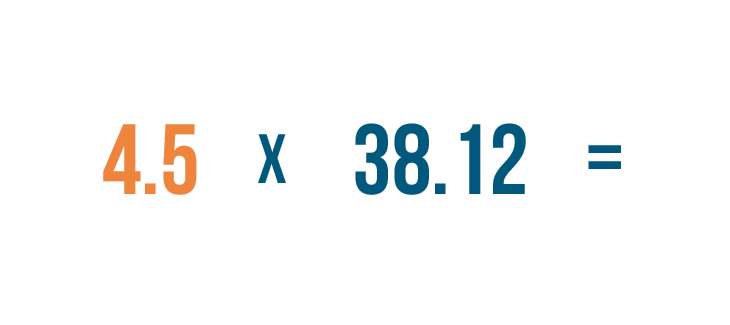
First, let's look to see how many digits are in each number. 4.5 has two digits...
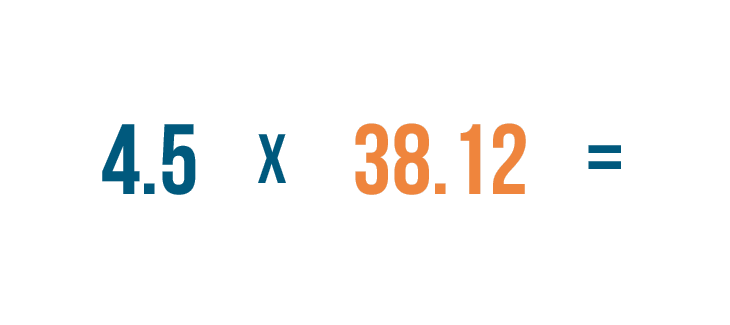
First, look to see how many digits are in each number. 4.5 has two digits...and 38.12 has four digits.
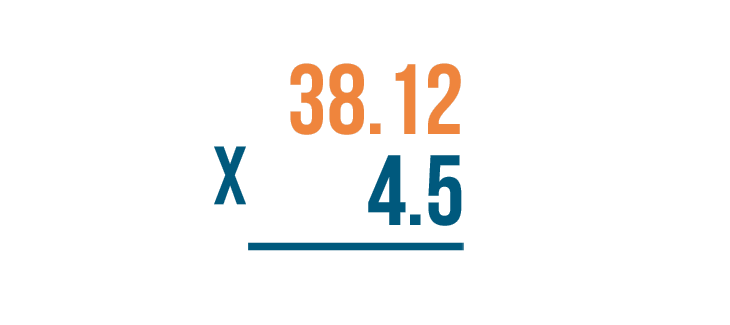
38.12 has more digits. This means we'll place 38.12 above 4.5.
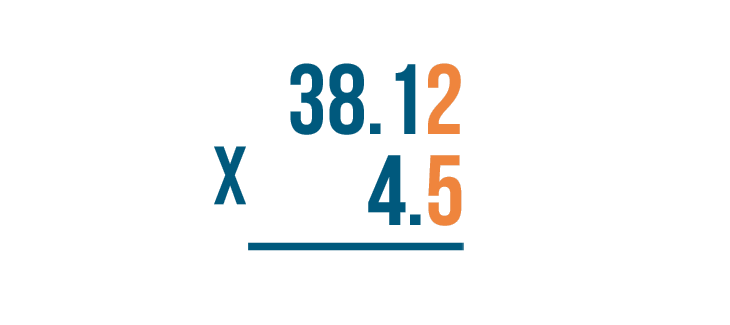
Then we'll make sure the digits to the right are lined up. The 2 is right above the 5.

Solving multiplication problems with decimals
Multiplying decimal numbers is a lot like multiplying larger numbers. If you divide the large problem into a few smaller ones, it will be easier to solve. Let's see how this works by solving this problem: 2.3 x 4.
Click through the slideshow to learn how to multiply decimals.
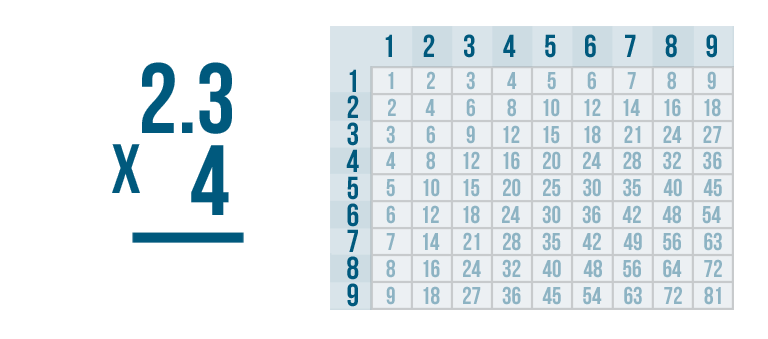
To solve our problem, we'll use a familiar tool: the times table.
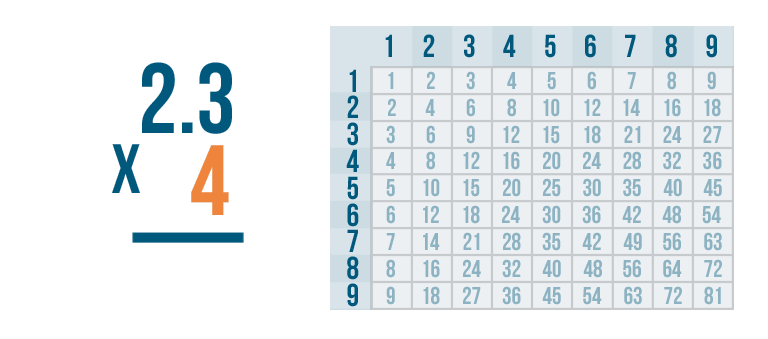
When multiplying stacked numbers, start with the right digit on the bottom. The bottom number only has one digit: 4.

We'll multiply 4 by the top number, 2.3. Since there's no 2.3 in the times table, we'll have to multiply one digit at a time.
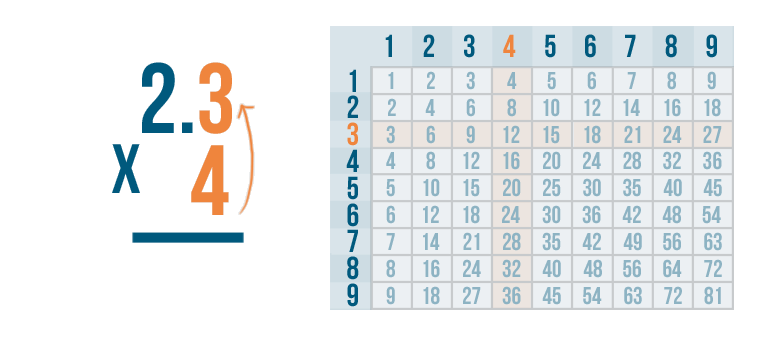
As usual, we'll solve the problem from right to left. So, we'll multiply 4 by the digit on the top right. Here, that's 3.

Now it's time to solve 4 x 3. We can use the times table.
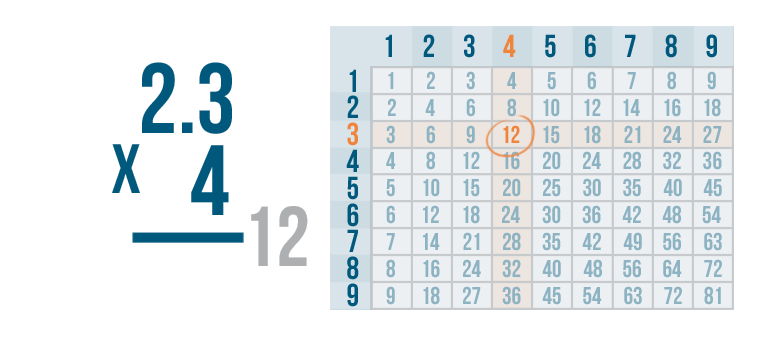
4 x 3 is 12, but there's no room to write both digits underneath the 4 and 3.

Remember, this means we'll have to carry. We learned about carrying numbers in the lesson on multiplying larger numbers.
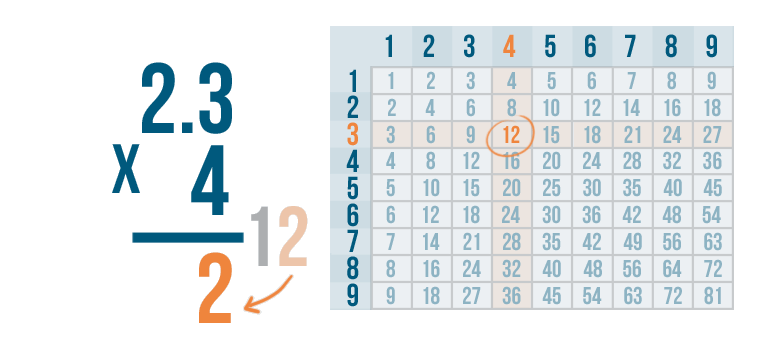
We'll write the right digit, 2, under the line...
We'll write the right digit, 2, under the line...then we'll carry the left digit, 1, up to the next set of digits in the problem.
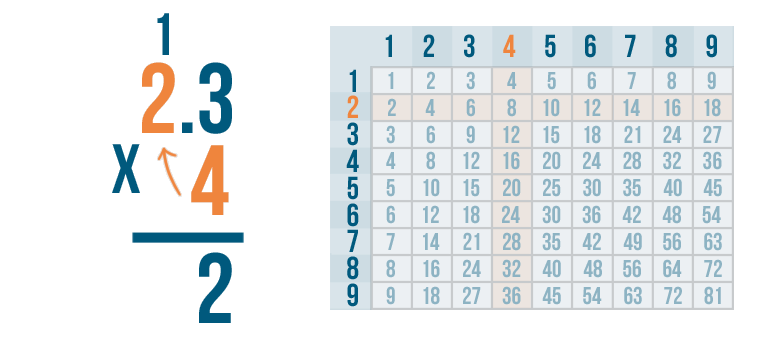
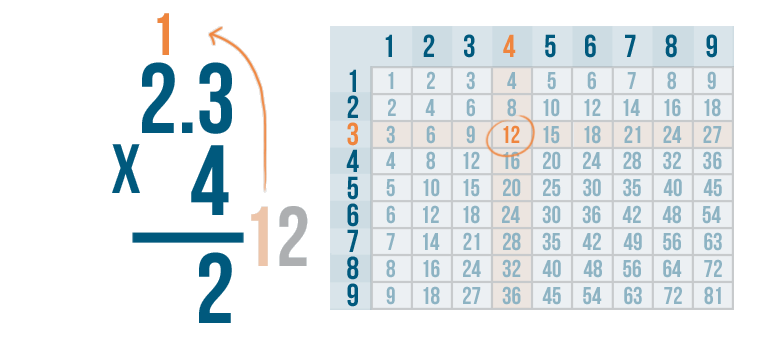
Now it's time for the next step. We'll multiply 4 x 2.
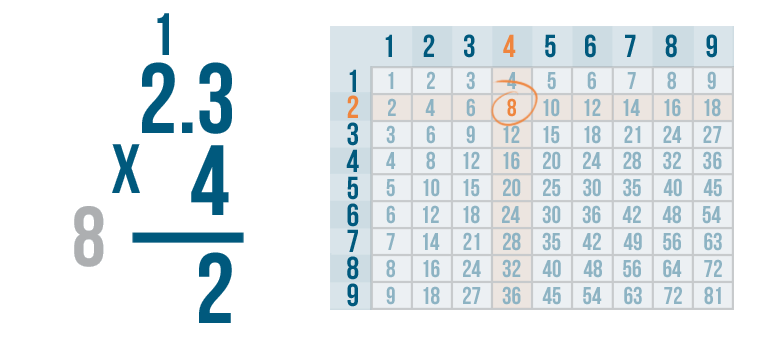
4 x 2 = 8. But we won't write 8 under the line yet. Remember, there's one more step.
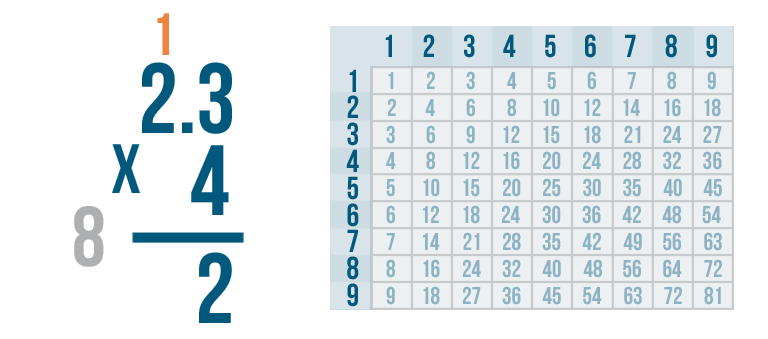
We need to make sure we add the number we carried: 1.
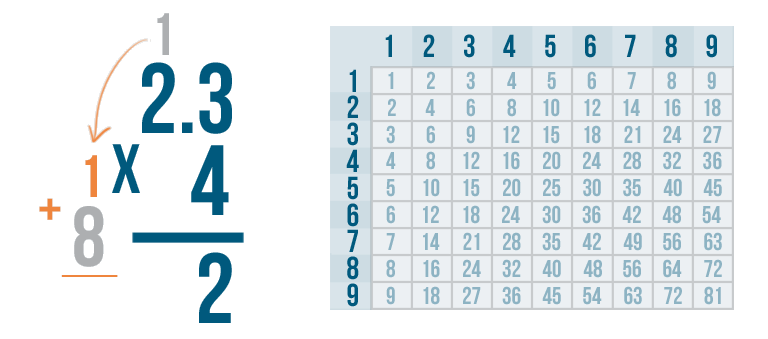
We'll set up our addition problem.
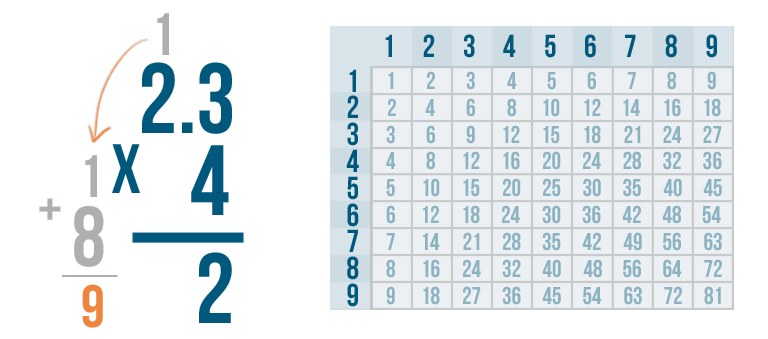
1 + 8 = 9.
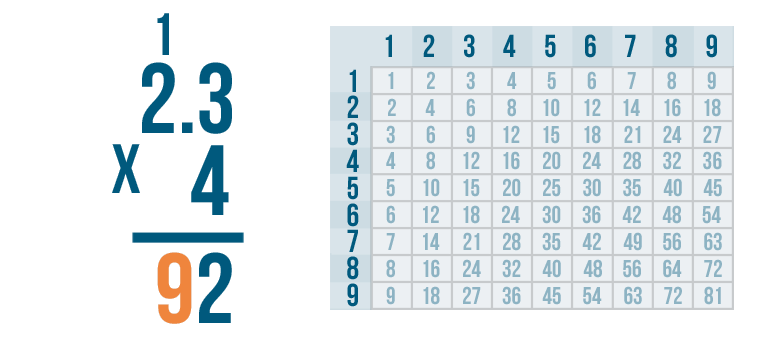
We'll write 9 beneath the line.

In our problem, we multiplied a decimal number: 2.3. This means our answer will also need to be a decimal number.

Let's figure out where to put the decimal point (.).
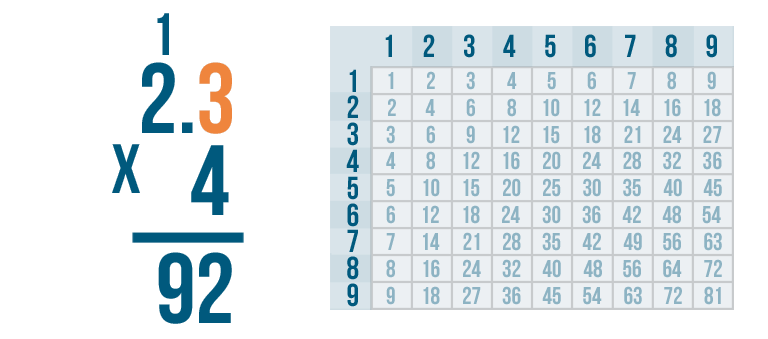
In the problem, 2.3 has one digit to the right of the decimal point.

This means our answer will also have one digit to the right of the decimal point.
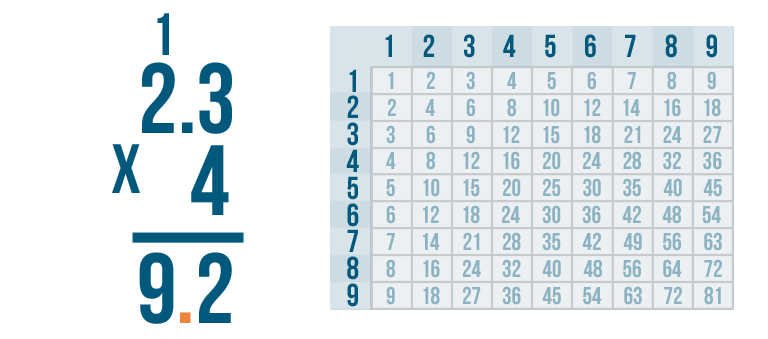
We'll place the decimal point so that only one digit is to the right: the 2.

Our problem is solved. The total is 9.2. We know that 2.3 x 4 = 9.2. We can read this answer as nine and two-tenths.
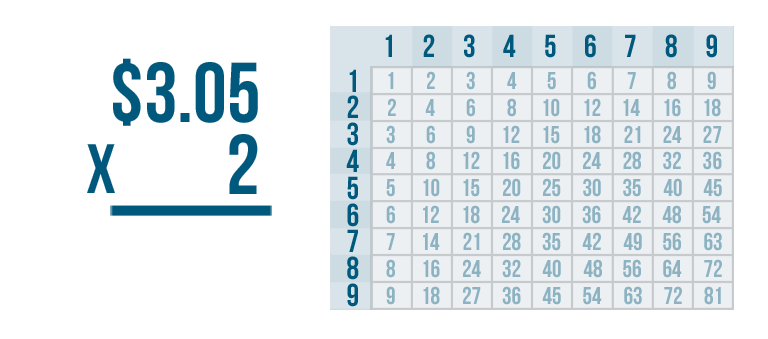
Let's try another problem. This time we'll multiply money: $3.05 x 2.
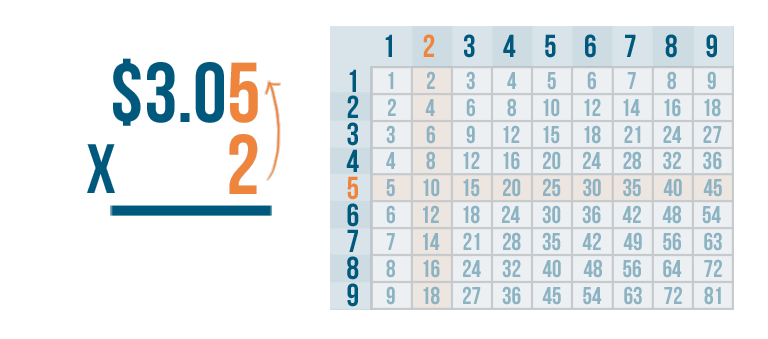
First, we'll multiply the bottom number, 2, by the digit on the top right. That's 5.
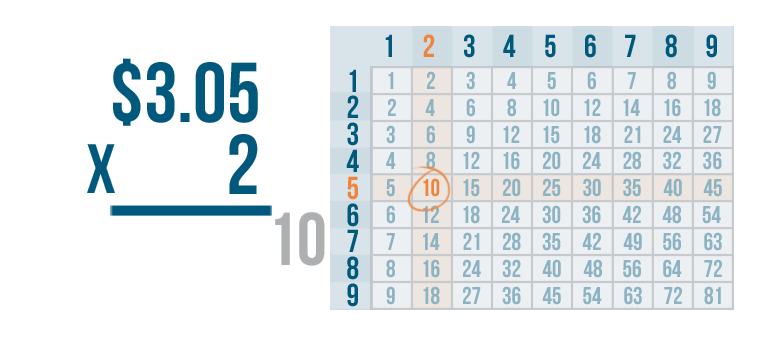
2 x 5 = 10.

We'll write the 0 under the line...
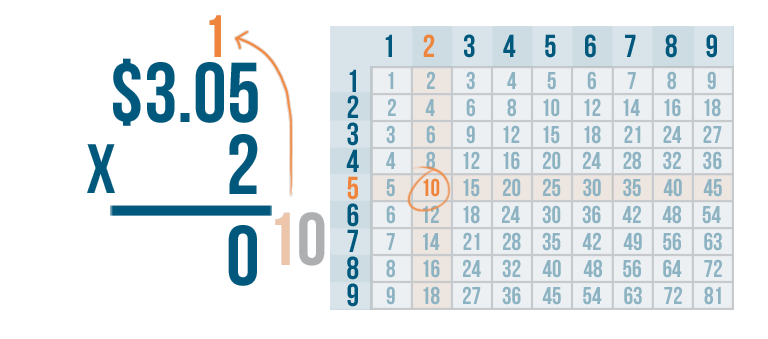
We'll write the 0 under the line...and carry the 1. We'll place it above the next digit.
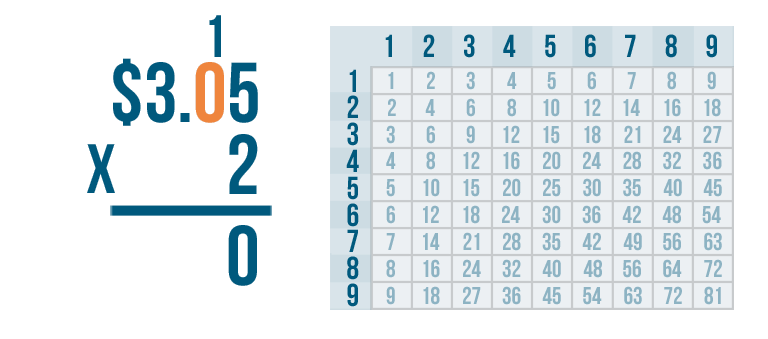
The next digit is 0.
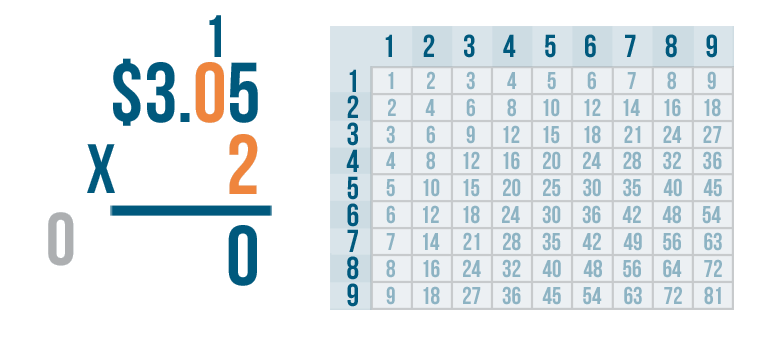
Anything times zero is zero, so we know that 2 x 0 = 0.
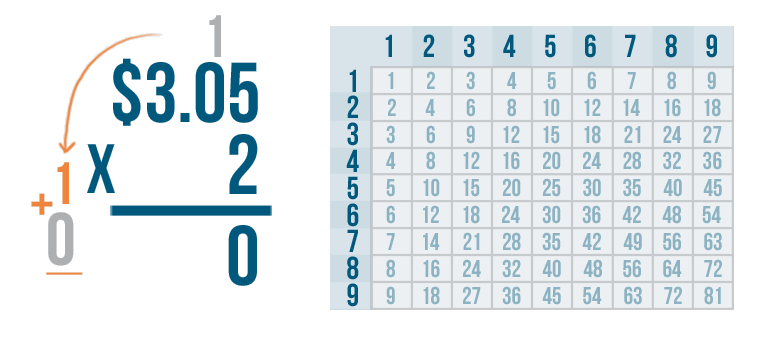
Remember, we need to make sure we add the 1 that we carried.
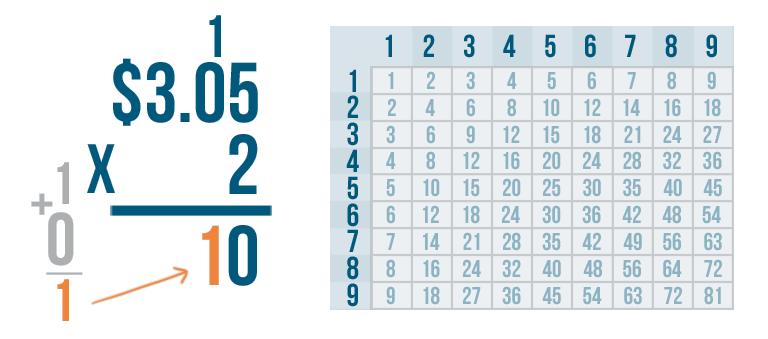
0 + 1 = 1. We'll write 1 beneath the line.
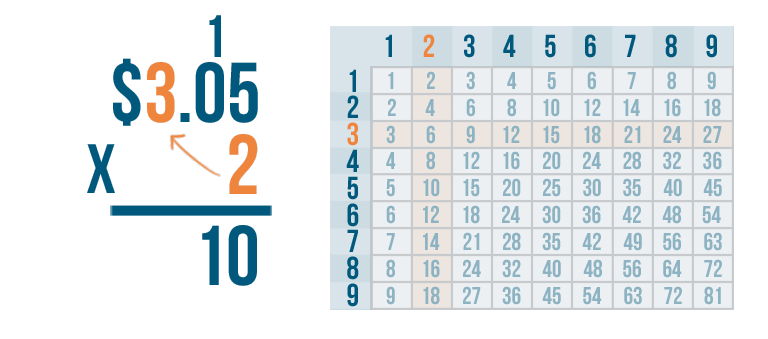
Finally, we'll multiply 2 and 3.
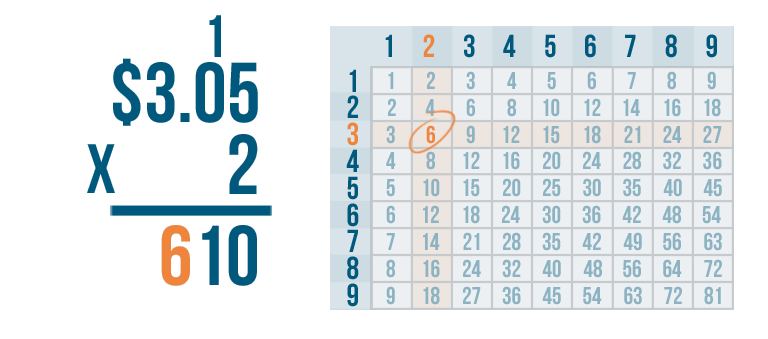
2 x 3 = 6, so we'll write 6 beneath the line.
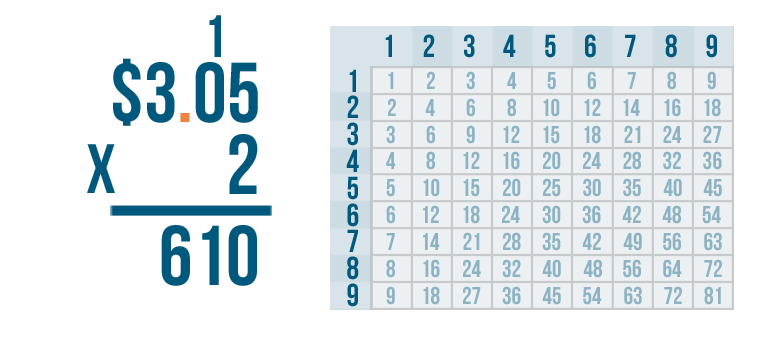
It's time to place our decimal point. We need to count the digits to the right of the decimal point in our problem.
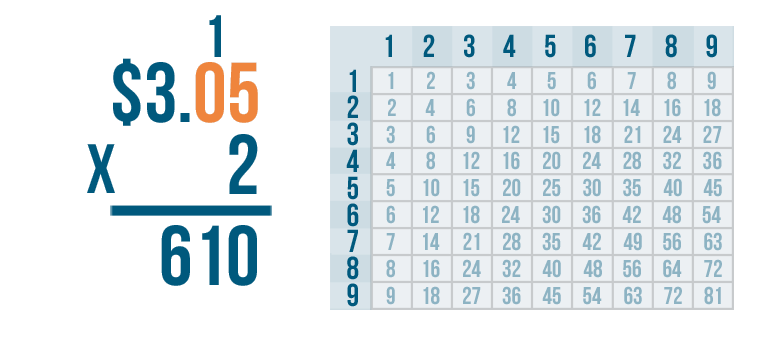
3.05 has two digits to the right of the decimal point. They're 0 and 5.

This means our answer will need to have two digits to the right of the decimal point.
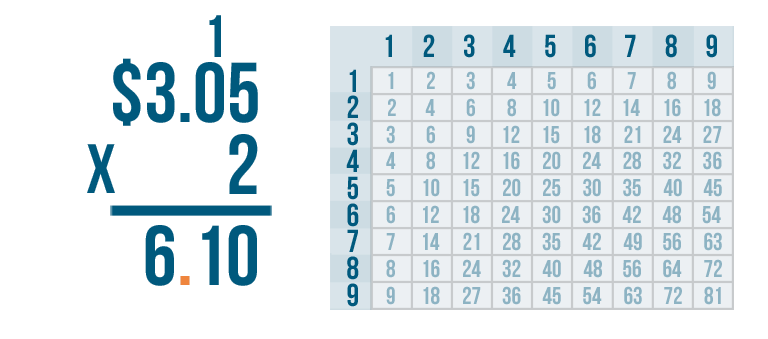
We'll place the decimal point so that two digits are to the right: the 1 and the 0.
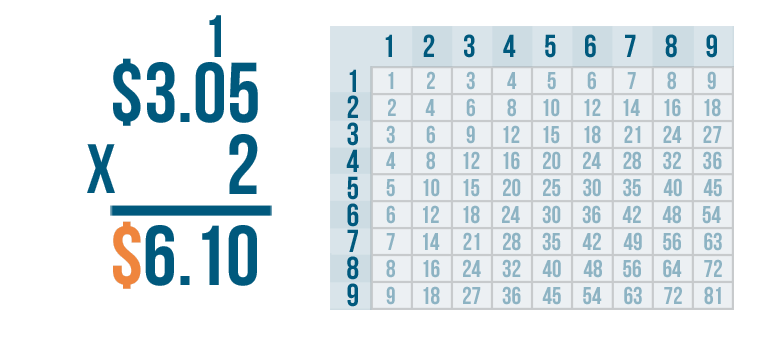
Finally, we'll write a dollar sign ($) to the left of the number.
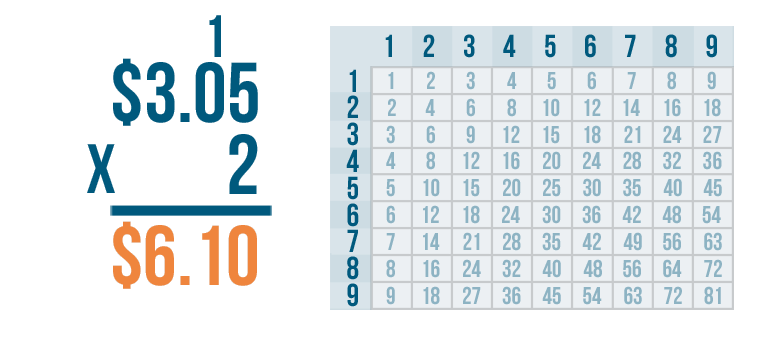
We've solved the problem. $3.05 x 2 = $6.10. We can read this as six dollars and ten cents.

Note: When determining where to place your decimal point in your answer, count the total number of digits to the right of each decimal point in your problem. For example, if you are simplifying 3.25 x 2.3, you would count the two digits in 3.25 plus the one digit in 2.3. Therefore, we should place the decimal point in our answer so that three digits are to the right (3.25 x 2.3 = 7.475).
Try This!
Try solving these multiplication problems. Then, check your answer by typing it in the box.
Dividing decimals
Let's look at a different situation. Let's imagine you have a fence, and you want to plant 5 bushes in front of it. Your fence is 20 feet long. You'd like to space the bushes out equally, so you know you'll need to divide your fence into 5 equal sections. This means you'll need to divide 20 by 5.
In the lesson on division, we learned how to set up division expressions. For the situation above, the expression would look like this:

In our expression, 20 is a whole number. But what if the length of the fence is a decimal number? For instance, let's say it's 20.75 feet long. Believe it or not, dividing a decimal isn't that different.
When you set up an expression to divide a decimal number, it's important to make sure you're always dividing by a whole number. In our example above, 20.75 is being divided by the whole number 5. Dividing by a whole number makes long division easier to manage.
Click through the slideshow below to learn how to set up division problems with decimals.

Let's set up this expression: 20.75 / 5.

We learned in the lesson on division that dividing numbers is easier when the expression is written a little differently.
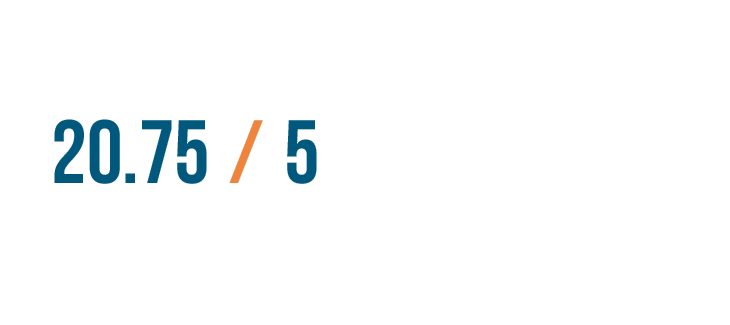
As usual, instead of writing the numbers side by side with a division symbol...

As usual, instead of writing the numbers side by side with a division symbol...we'll use the division bracket.
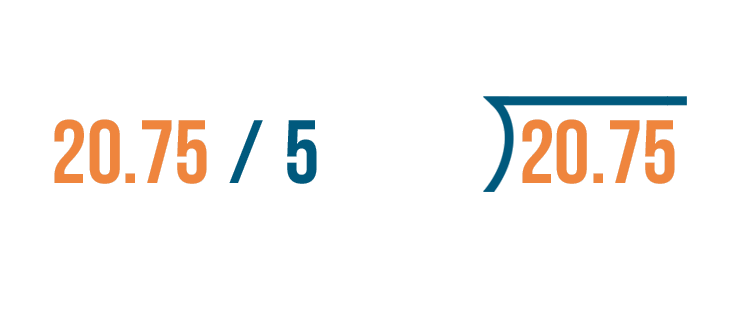
The number we're dividing goes under the division bracket. That's 20.75.
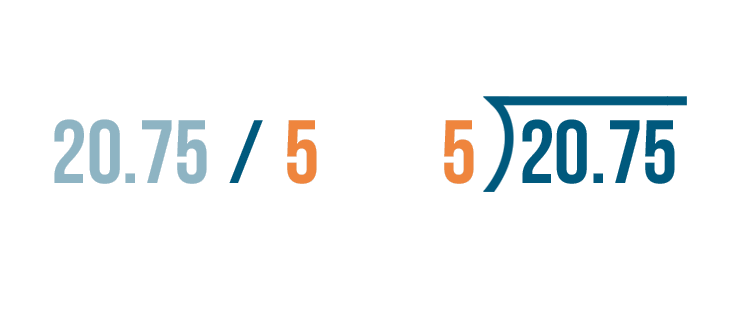
To the left of the division bracket, we'll write the number we're dividing by. In our problem, it's 5.
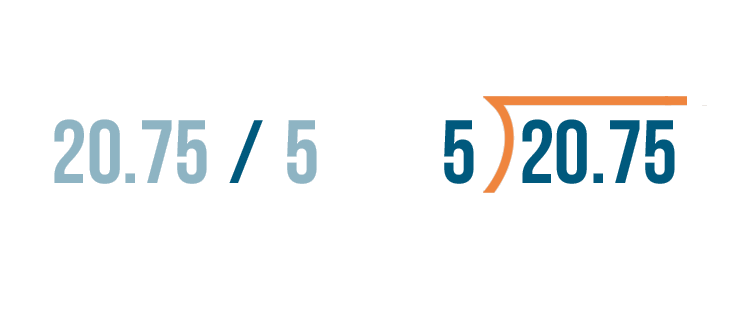
Remember, the division bracket is also an equals sign.
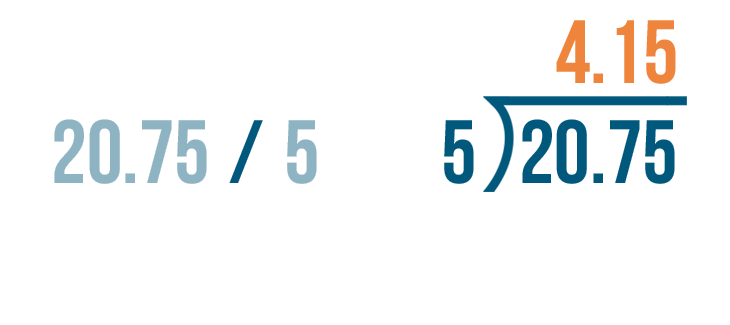
The quotient, or answer, is written above it.

Let's set up another expression. This time, both numbers are decimal numbers: 80.1 / 4.2.

First, we'll write the division bracket.

Next, we'll write the number being divided: 80.1.

Finally, we'll write the number we're dividing by: 4.2.

Since we're dividing a decimal number by a decimal number, there's one more step we need to do.

To make division easier, we'll change the the number we're dividing by into a whole number. This means we'll change 4.2.

To make 4.2 a whole number, we'll need to move the decimal point so it comes after the last digit in the number.

This means we'll move it so it comes after the 2.

Now all of the digits are to the left of the decimal point. We've created a whole number. 4.2 becomes 42.

A whole number is usually written without a decimal point after it...

A whole number is usually written without a decimal point after it...so we'll drop the decimal point.

See how we did that? We moved the decimal point to the right and then dropped the decimal point.

Since we moved the decimal point in one number...

Since we moved the decimal point in one number...we'll also need to move the decimal point in the other number: 80.1.

So we'll move this decimal point the same number of times.

80.1 becomes 801.

801 is a whole number, so we'll drop the decimal point.

Now the division expression is 801 / 42.

Moving decimals can be tricky, so it's important to change the number you're dividing by into a whole number first.

Let's try it one more time with a different expression: 0.4 / 0.02.

First, we'll change 0.02 into a whole number.

We'll move the decimal point one time to the right.
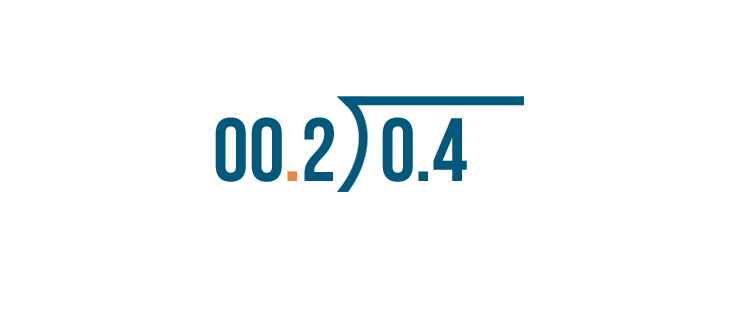
0.02 becomes 0.2.

We still have a digit to the right of the decimal point: 2. This means our decimal isn't a whole number yet.

So we'll move the decimal point to the right a second time.

0.2 becomes 2. All of the digits are now to the left of the decimal point.

The zeroes and the decimal point are no longer needed. We'll drop them.

Since we moved the first decimal point two times to the right...

Since we moved the first decimal point two times to the right...we'll do the same to the second decimal point.

We'll move it one time...

We'll move it one time...then we'll add a zero...

We'll move it one time...then we'll add a zero...and then we'll move it a second time.
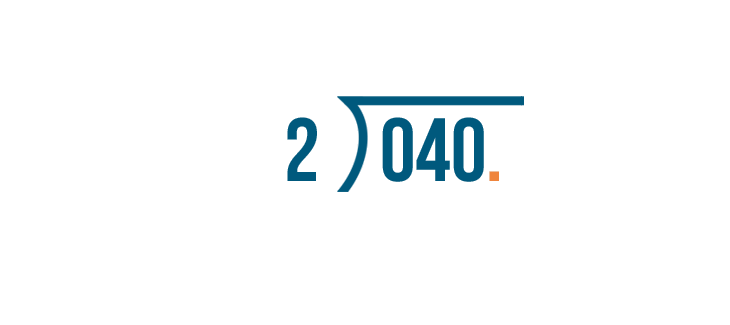
0.4 becomes 40.

Since 40 is a whole number, we'll drop the zero and the decimal point.
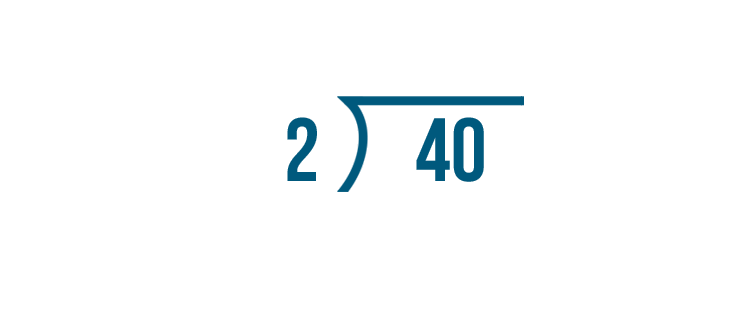
The division expression is now 40 / 2. Our problem is ready to be solved.

Dividing decimal numbers
In the previous slideshow, you practiced setting up division expressions with decimal numbers. Let's take a closer look at how to divide a decimal. Dividing a decimal number is a lot like dividing a whole number. There's just one extra step at the end.
Click through the slideshow to learn how to divide decimals.
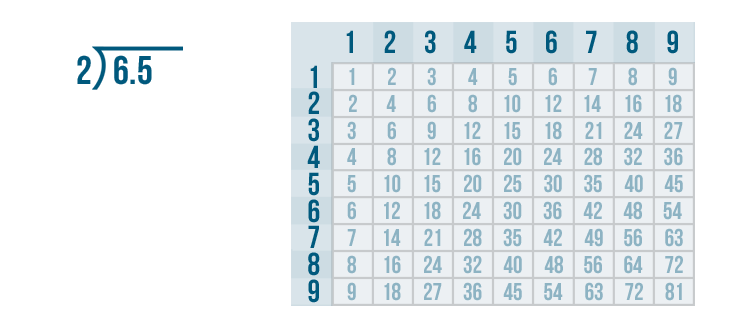
We'll use long division to solve this problem: 6.5 / 2.

We learned in the lesson on long division that when solving a long division problem, we'll follow a pattern until the problem is complete.
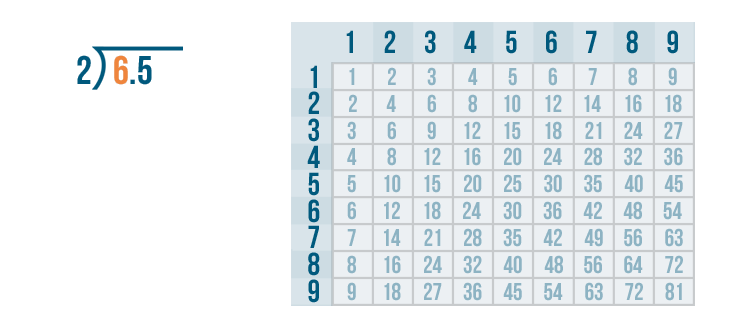
We'll begin with the left digit under the division bracket. This means we'll start with the 6...
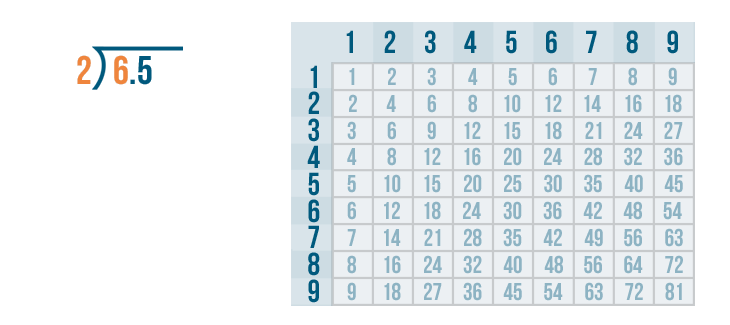
We'll begin with the left digit under the division bracket. That means we'll start with the 6...and we'll figure out how many times it can be divided by 2.
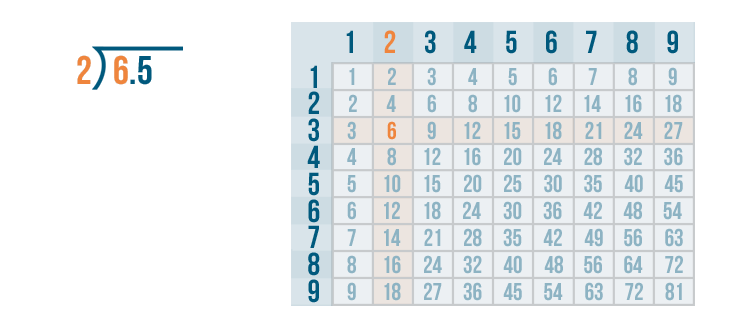
We'll use the times table to help us. Remember, if you need to review how to use the times table, you can revisit the lesson on multiplication. Now it's time to solve 6 / 2.
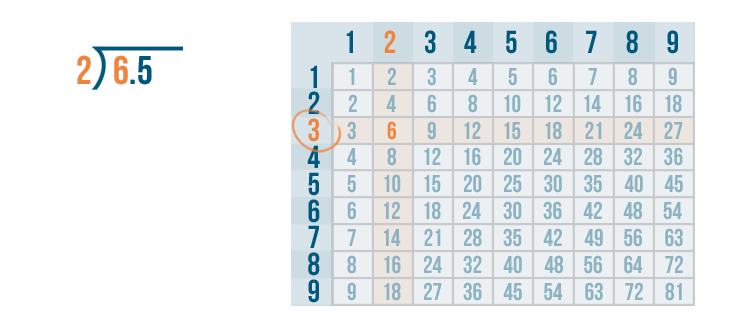
6 / 2 = 3.
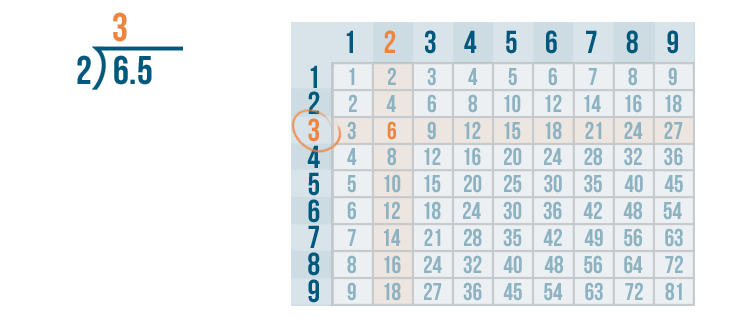
We'll write 3 above the 6.
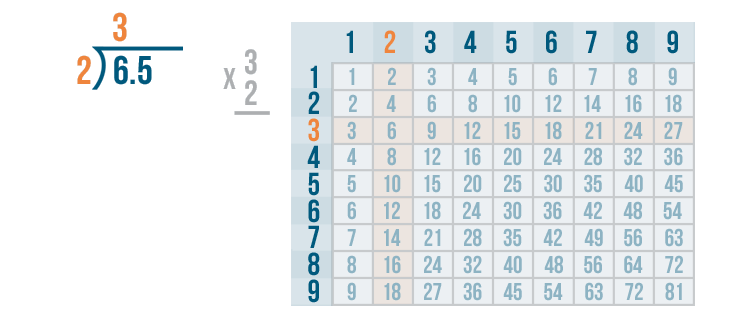
Next, we'll multiply the 3 and 2.
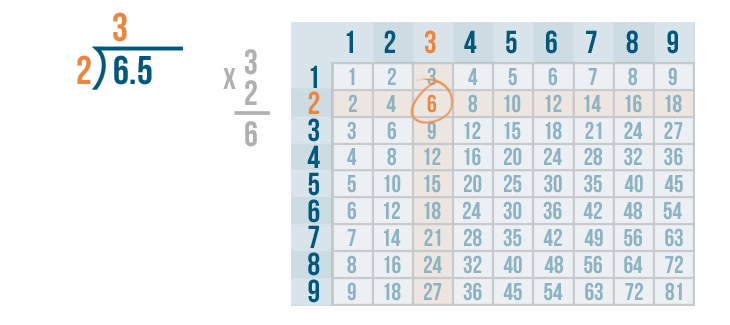
3 x 2 = 6.
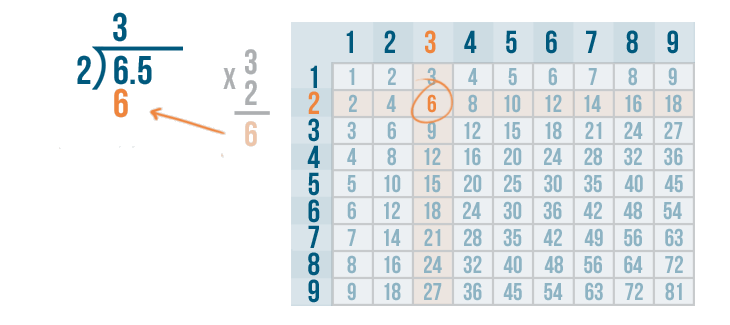
We'll write 6 below the 6.
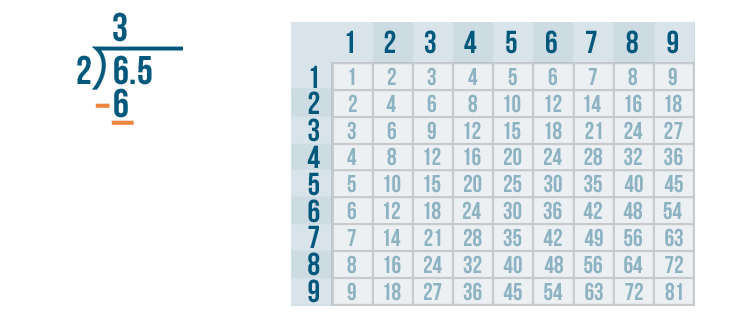
Next, we'll set up our subtraction problem.
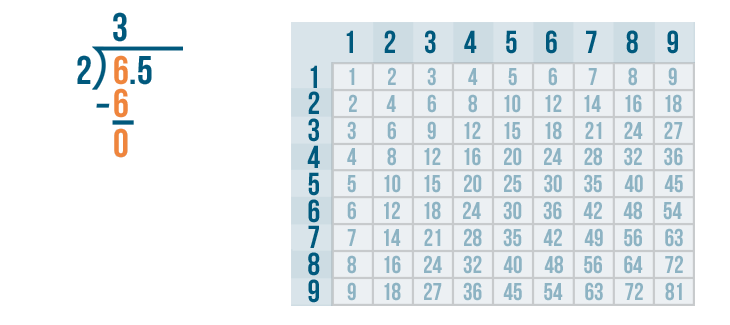
6 - 6 = 0. We'll write 0 below the line.
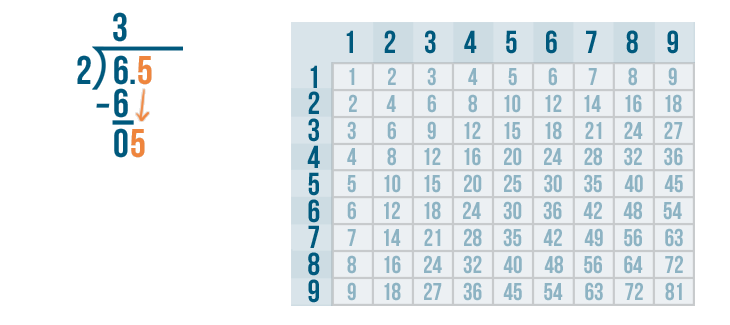
Now, we'll bring the 5 down and rewrite it next to the 0.
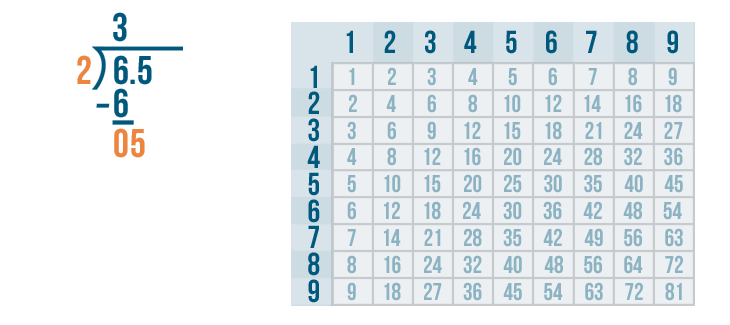
05 means the same as 5. 5 is large enough to be divided, so we'll figure out how many times 5 can be divided by 2.
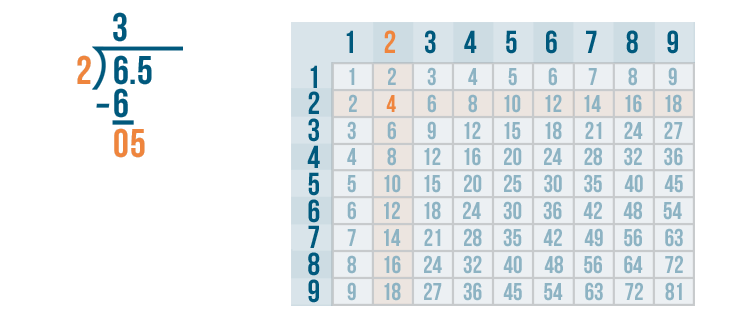
In the 2's column, we'll look for the number that's the closest to 5 but no larger than 5. That's 4.
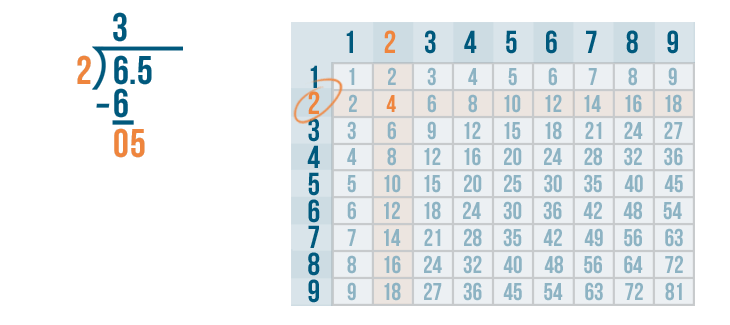
4 is in the 2's row. That means 2 goes into 5 two times.
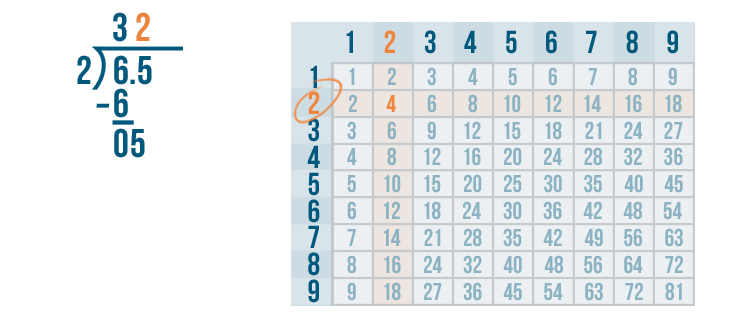
We'll write 2 above the 5.
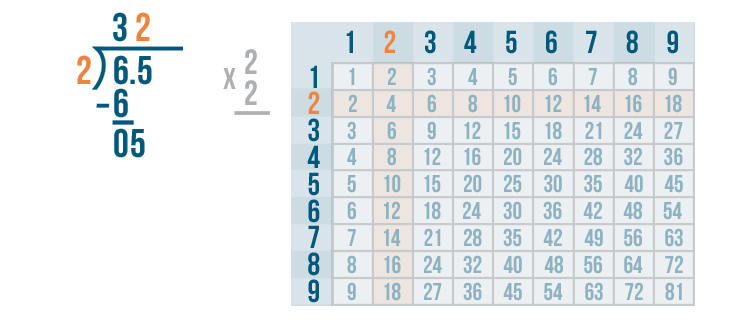
Now it's time to multiply the 2 and 2.
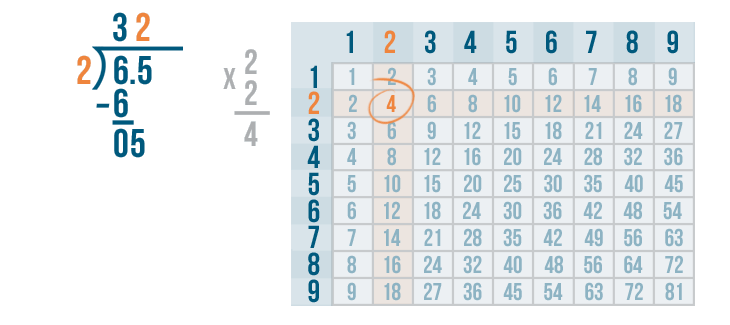
2 x 2 = 4.
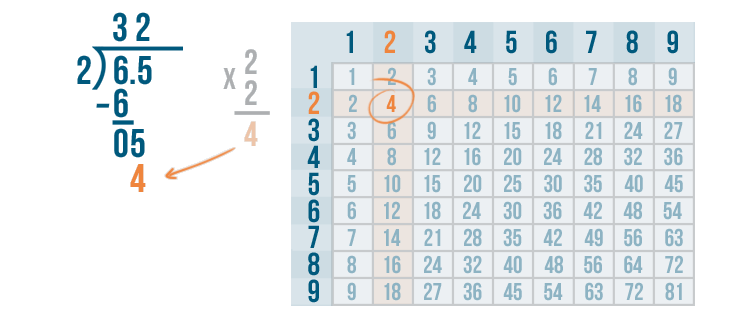
We'll write 4 beneath the 5.
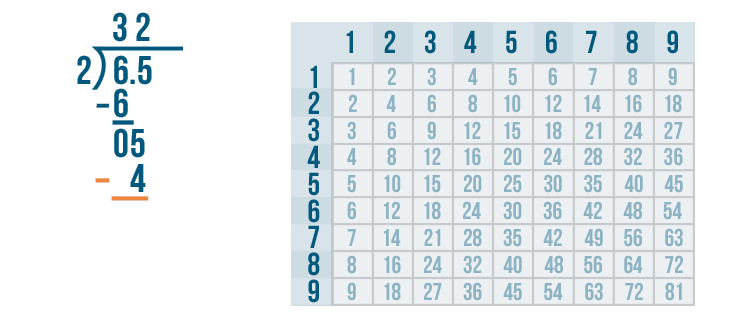
Now it's time to set up our subtraction problem.
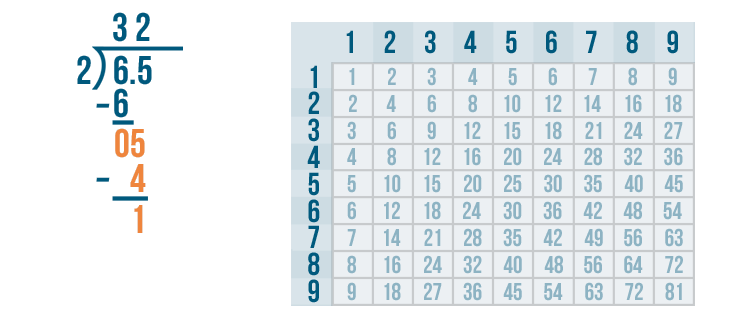
5 - 4 = 1. We'll write 1 beneath the line.
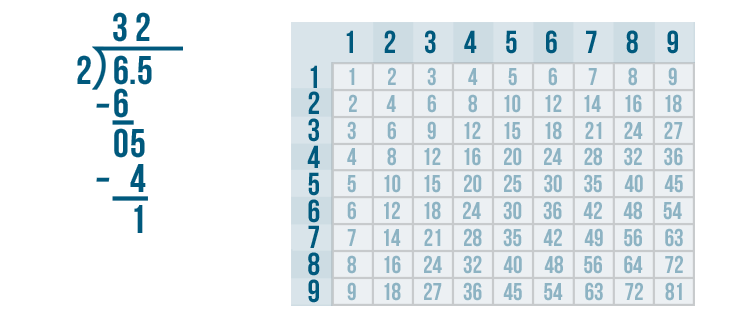
Since our answer to the subtraction problem is 1, we'll look under the bracket to see if there is another digit we can bring down.

There are no more digits for us to bring down. We learned in the long division lesson that we can write a zero next to the number under the division bracket.
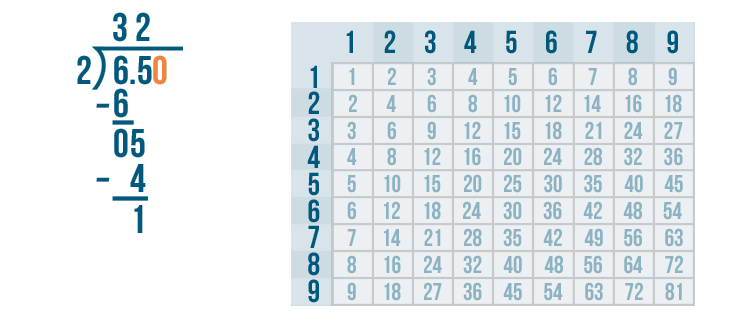
So next to 6.5 we'll write 0.
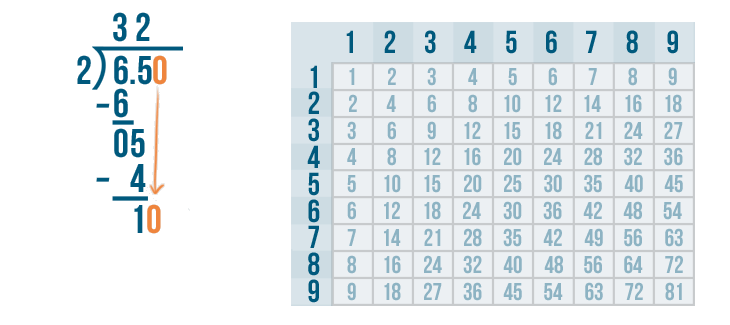
Now we can continue solving this problem. We'll bring the 0 down and rewrite it next to the 1.
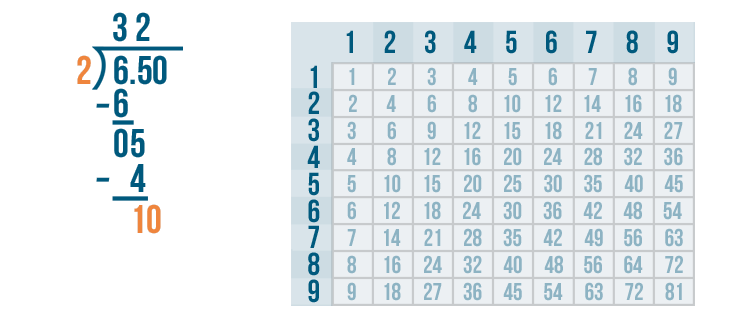
Let's see how many times 10 can be divided by 2.
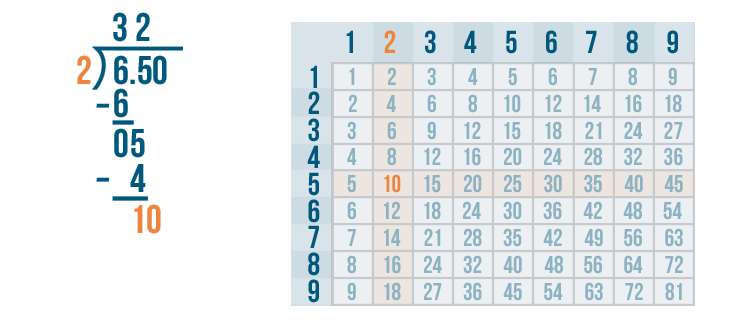
In the 2's column, we'll look for the number that's the closest to 10 but no larger than 10. There's a 10 in the 2's column. That's exactly what we need!
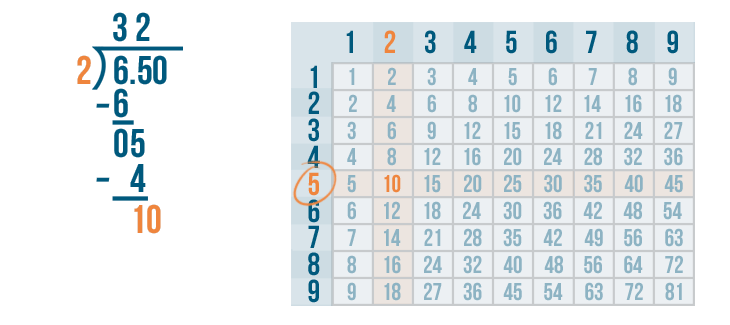
10 is located in the 5's row. This means 2 goes into 10 five times.
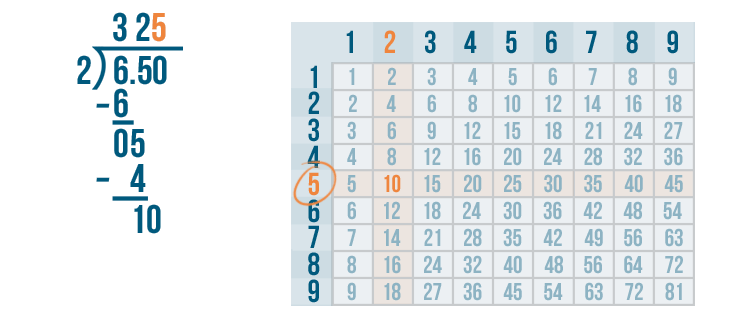
We'll write 5 above the 0.
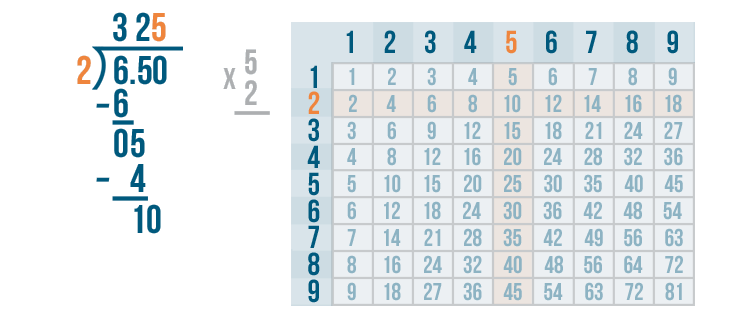
Now it's time to multiply the 5 and 2.
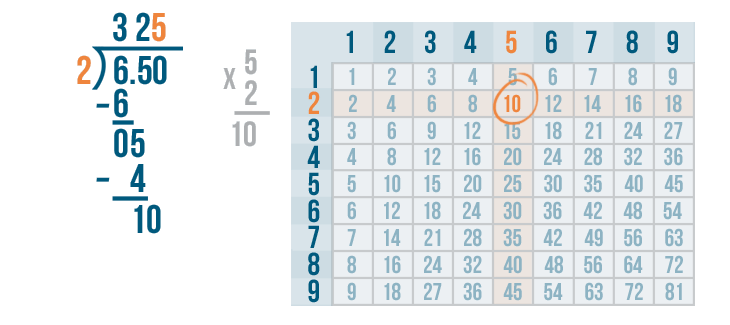
5 x 2 = 10.
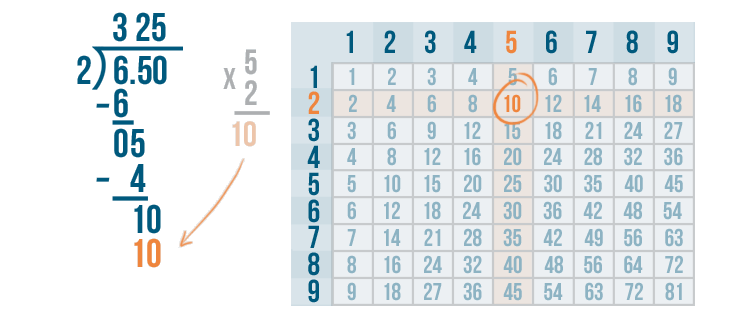
We'll write 10 beneath the 10.
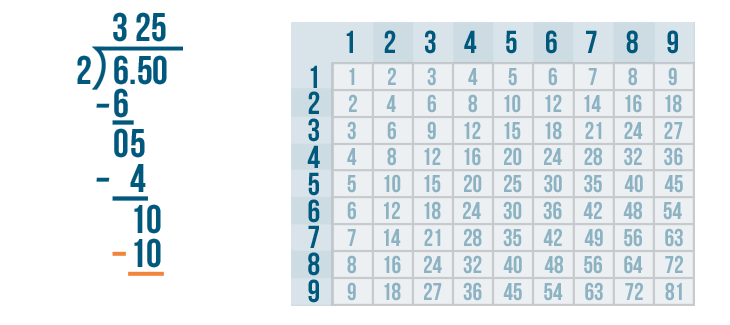
Next, we'll set up the subtraction problem.
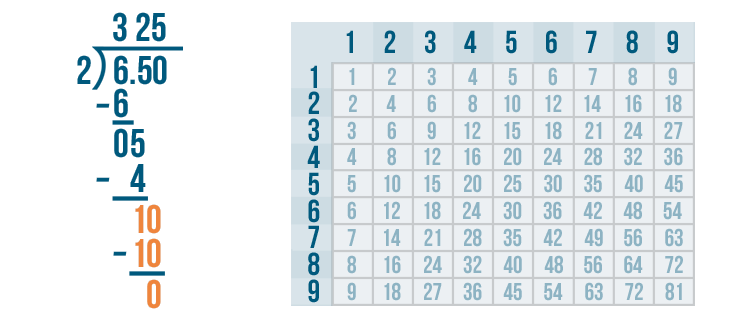
Now it's time to solve. 10 - 10 = 0.
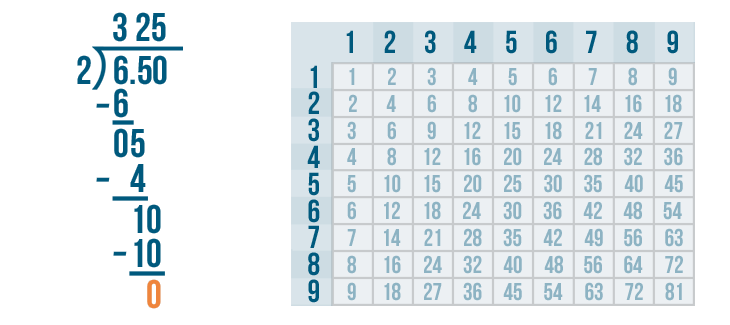
Since the answer to the subtraction problem is 0 and there are no more digits to bring down, we're done dividing. There's just one last step we need to do.
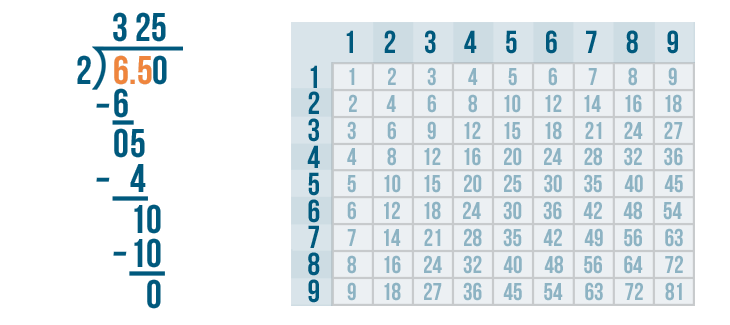
In this problem, we divided a decimal number: 6.5. This means our quotient, or answer, will have a decimal point.
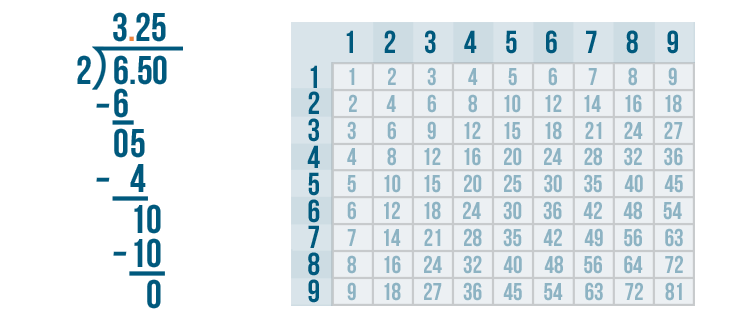
We'll simply write a decimal point directly above the other decimal point. See where we put it between the 3 and 2?
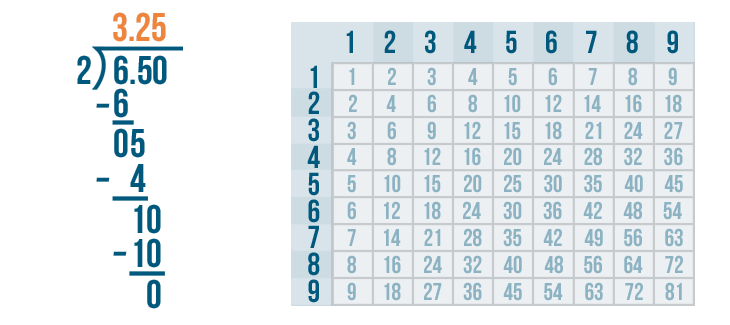
We've completed the problem. The quotient is 3.25. So 6.5 / 2 = 3.25. We can read this as three and twenty-five-hundredths.

Try This!
Find the quotient for each of the long division problems below. Check your answer by typing it in the box.
/en/decimals/converting-percentages-decimals-and-fractions/content/





