Algebra Topics -
Writing Algebraic Expressions

Algebra Topics
Writing Algebraic Expressions


/en/algebra-topics/reading-algebraic-expressions/content/
If you're learning algebra in school or are studying for a test, you've probably notice that many problems ask you to translate written words into algebraic expressions. In other words, there are plenty of word problems.
Some word problems have real-life details—almost like a short story. Others are simple, like descriptions of a math problem. We'll start with simple word problems, then move on to slightly more complex ones.
Before you can tackle complex word problems, you need to know how to translate simple problems into algebra. Generally, you'll do this by replacing the words with operators that mean the same thing. So for instance, four divided by x could be 4 ÷ x. ÷ and / are just two ways of writing divided.
Here are some of the most common math words you'll see:
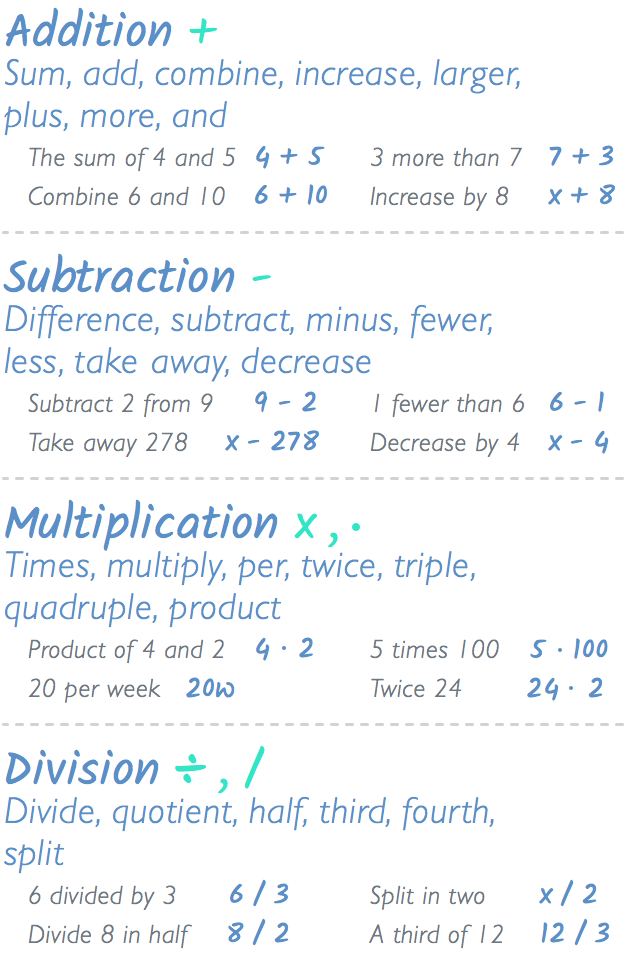
Many of these are probably familiar to you in everyday conversation. For instance:
Some expressions are slightly more complicated than the ones we looked at on the last page. For instance, some expressions include more than one math operation. Take this one as an example:
Five times the sum of four and two
If you were to translate this word for word, you'd change the word times to a multiplication symbol (⋅) and put a plus sign (+) between the four and the two. Your expression would look like this:
5 ⋅ 4 + 2
However, this wouldn't get us the right answer. This is because the order of operations would call for you to multiply 5 times 4 first, then add 2. However, our written expression asks us to multiply 5 by the sum of 4 and 2. In other words, we need to add 4 and 2 first, then multiply that number by 5.
If you're familiar with algebraic notation, you know that parentheses are useful in cases like this—they let you group part of an expression and solve it separately from the rest. Here, we can use them to group 4 and 2—the numbers being added.
5 ⋅ (4 + 2)
This is the correct way to write the expression. Based on the order of operations, always solve operations in parentheses first. Here, you'd add 4 + 2, then multiply that sum by 5—in other words, exactly what was written in the original expression.
/en/algebra-topics/simplifying-expressions/content/