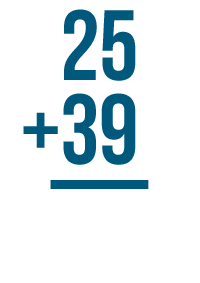Lesson 2: Adding Two- and Three- Digit Numbers
/en/additionsubtraction/introduction-to-addition/content/
Adding larger numbers
As we saw in Introduction to Addition, you can often use counting and visuals to solve basic addition problems. For instance, imagine that 3 people are going on a trip and 2 more decided to join. To find out how many people were going total, you could represent the situation like this:
Once you look at the problem visually, you can count and see that 5 people are going on the trip.
What if you have a bigger problem to solve? Imagine that a few groups of people are going somewhere together. 30 people travel on one bus, and 21 travel on another. We could write this as 30 + 21.
It might not be a good idea to solve this problem by counting. First of all, no matter how you choose to count, it would probably take a pretty long time to set up the problem. Imagine drawing 30 and 21 pencil marks on the page, or counting out that many little objects! Second, actually counting the objects could take long enough that you might even lose track.
For this reason, when people solve a large addition problem, they set up the problem in a way that makes it easier to solve one step at a time. Let's look at the problem we discussed above, 30 + 21.
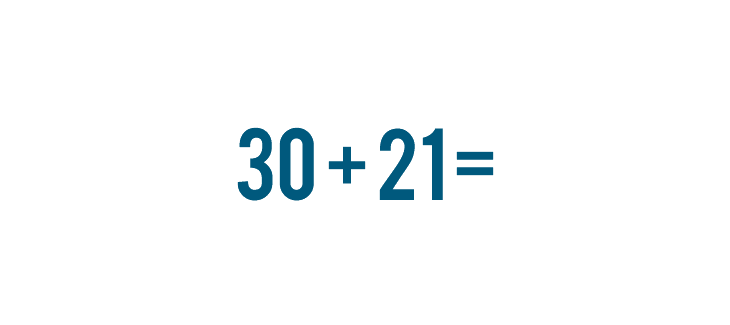
In the last lesson, we learned how to write expressions. However, when we're adding larger numbers, it helps to write the expressions in a different way.
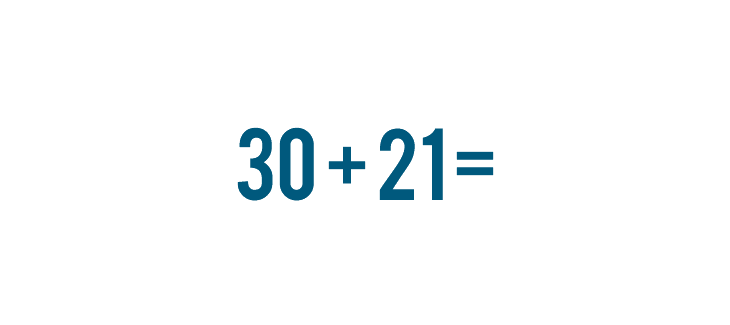
Instead of writing the numbers side by side...
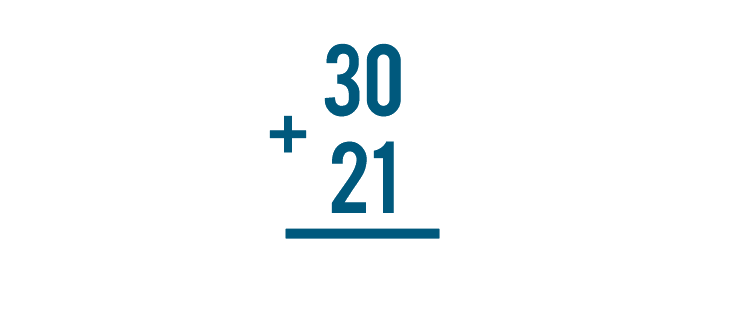
...We stack them on top of one another.
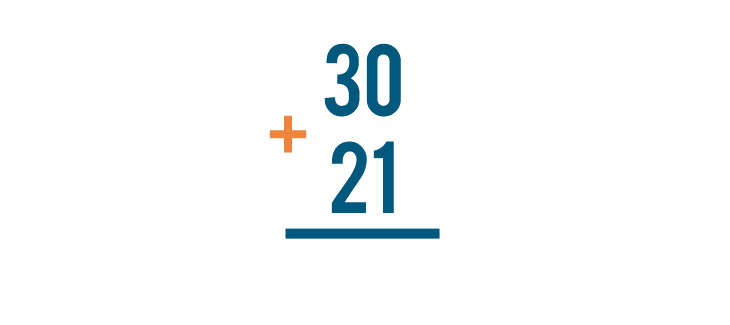
Put the plus sign (+) to the left of the numbers.
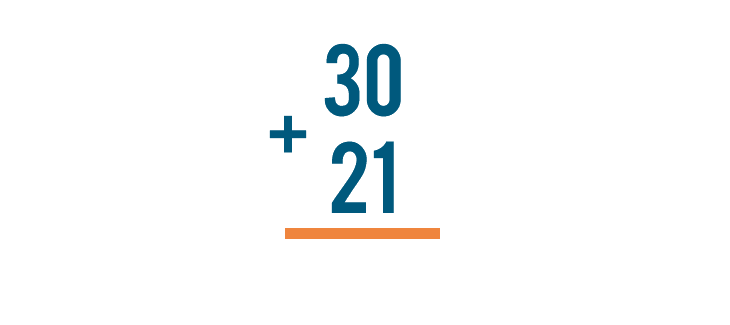
Instead of an equals sign (=), put a line underneath the lower number.
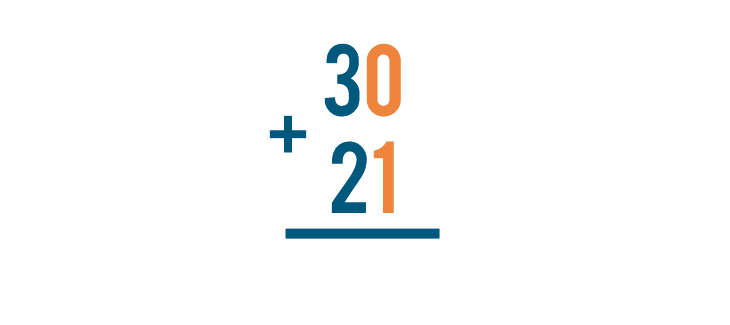
When you stack an addition expression, make sure the numbers are lined up correctly. The numbers should always be lined up on the right.
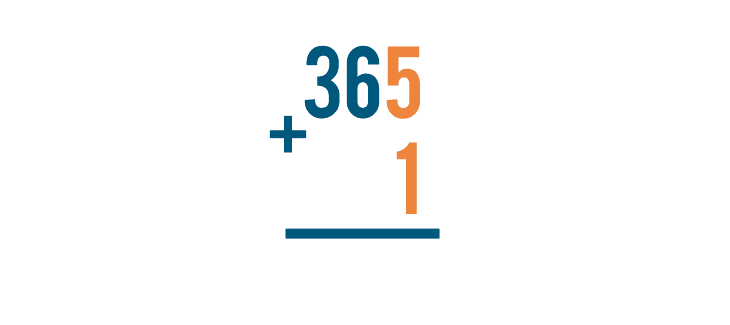
Let's look at another problem, 365 + 1. See how the 1 is under the 5?
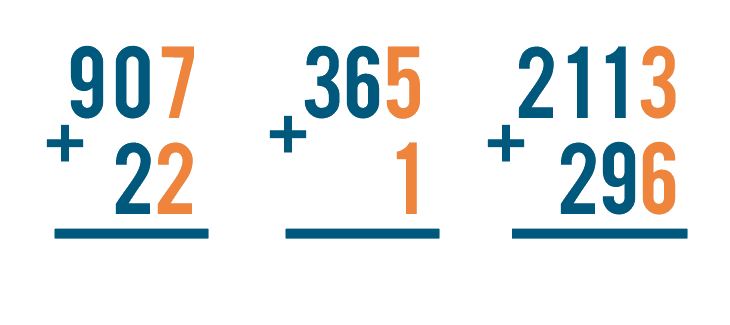
No matter how large the numbers you're adding are, the digits on the right should always be lined up.

We can see that 30 + 21 and 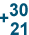 mean the same thing. They're just written differently.
mean the same thing. They're just written differently.
Solving Stacked Addition Problems
To solve stacked addition problems, all you need are the skills you learned in Introduction to Addition.
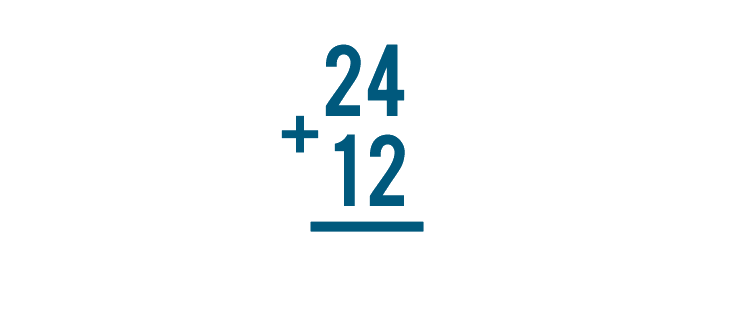
Let's try solving this problem, 24 + 12.
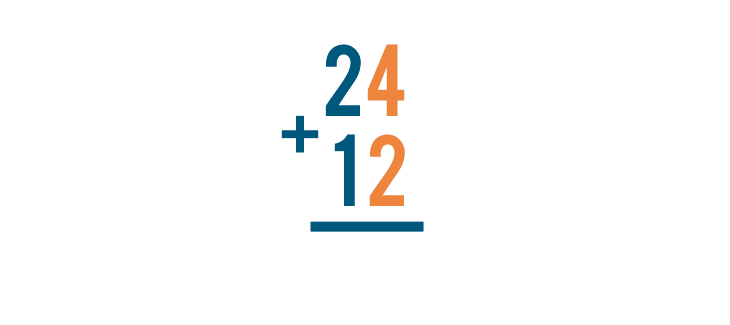
To solve a stacked addition problem, start by adding the digits farthest to the right.
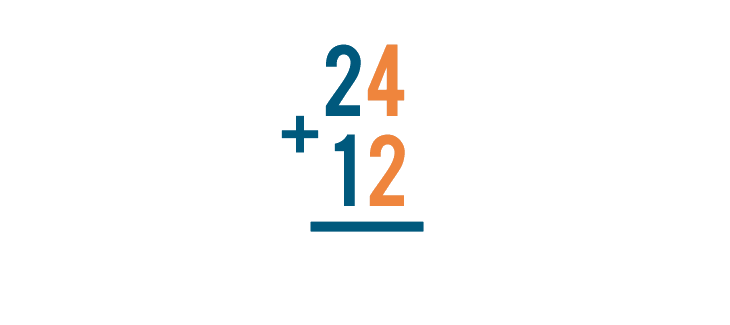
In this case, that means we'll add 4 and 2.
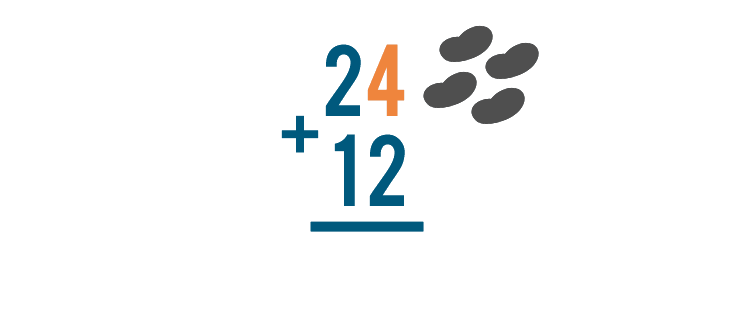
Like with any addition problem, we can use counting to help us add. Since our first digit is 4, we'll start with four objects.
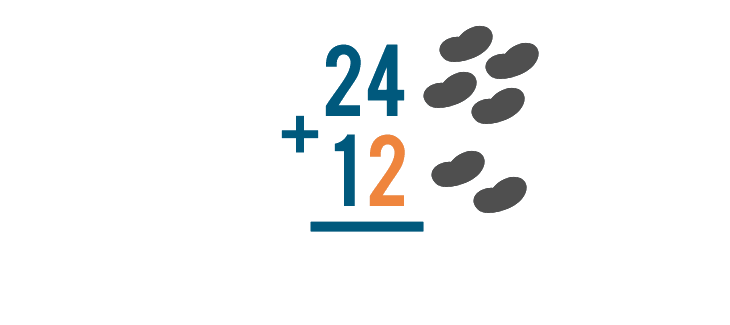
We're adding 4 to 2, so we'll use two more objects.
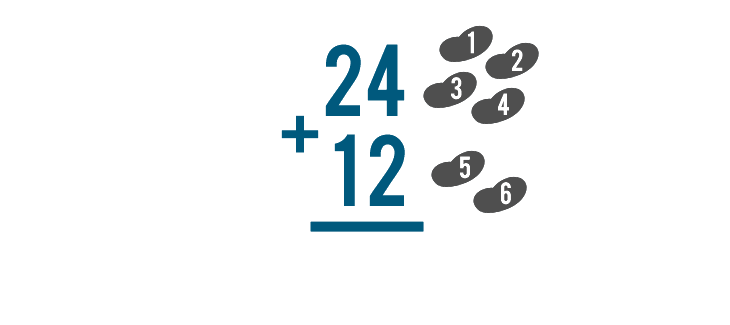
We can count to get a total of 6. We know that 4 + 2 = 6.
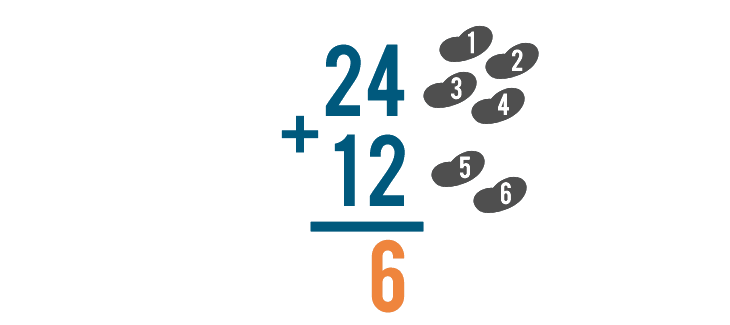
Write 6 under the line. It's important to put it directly beneath the numbers we just added.
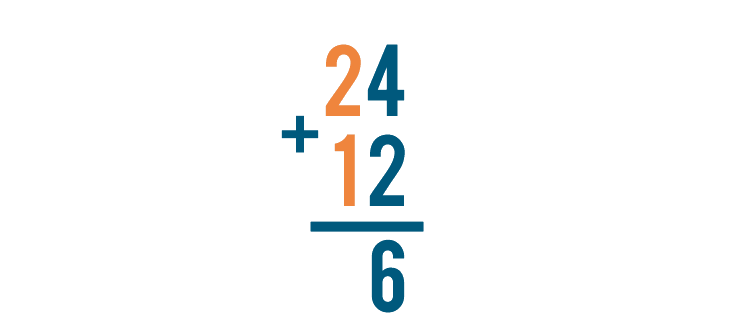
Next, we'll add the digits to the left of the ones we just added. That's 2 and 1.
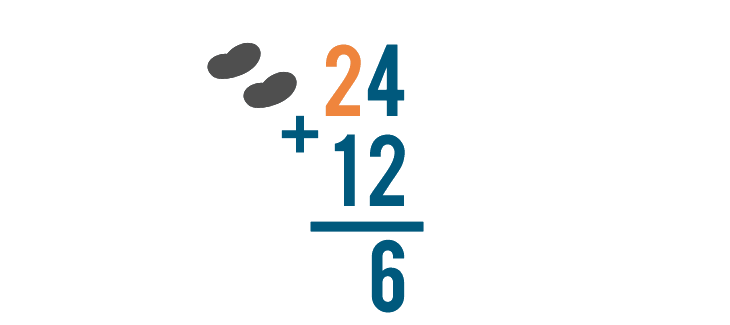
We'll use two objects to show the 2.
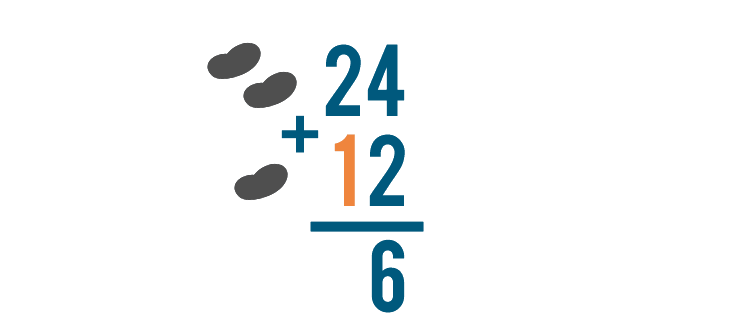
Next, we'll add one object to represent the 1.
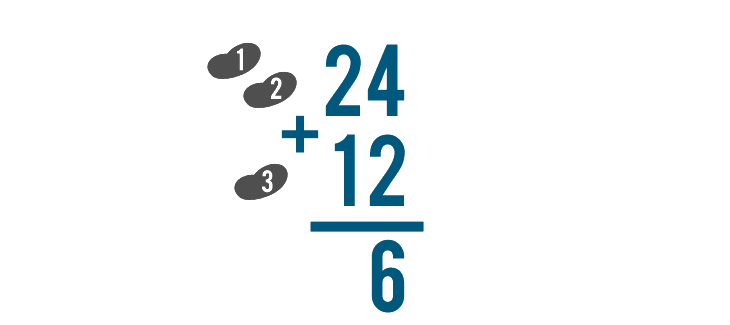
When we count, we get 3.
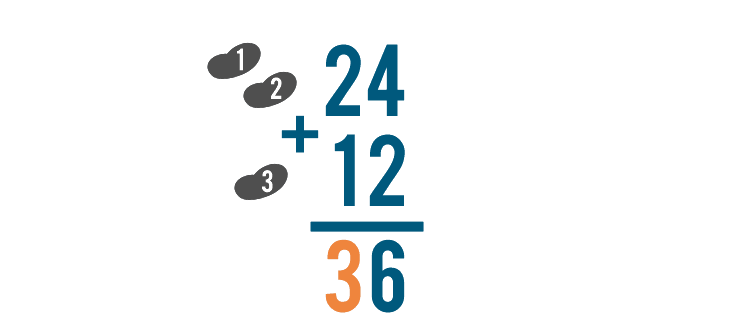
We'll write the 3 under the line, beneath the 2 and 1.
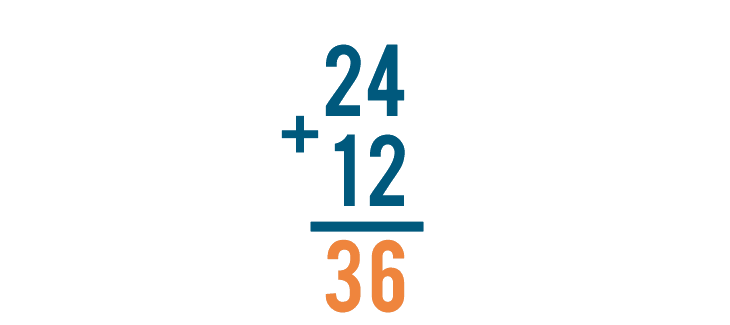
We're done! Our total is 36, or thirty-six.
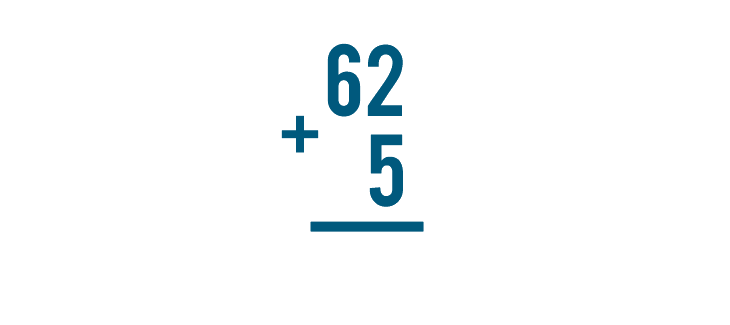
Let's look at one more problem, just for practice. This time, we'll solve 62 + 5.
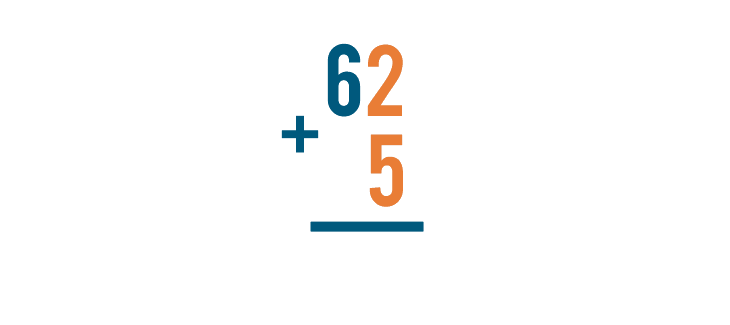
We'll start by adding the digits on the right, 2 and 5.
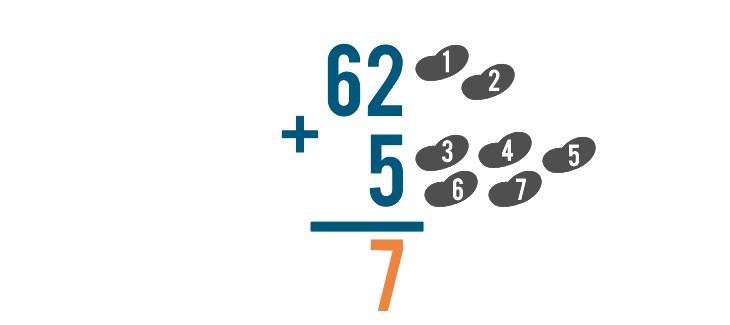
2 + 5 is 7.
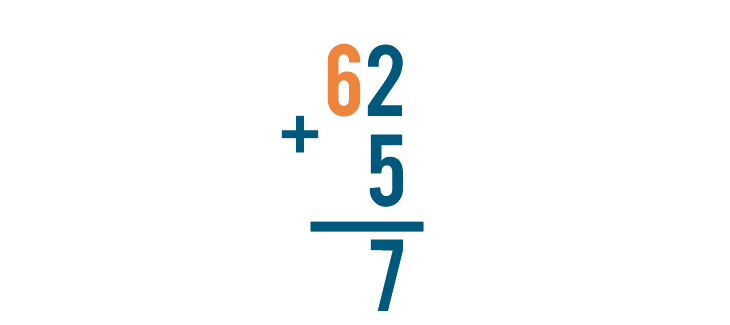
Now, let's add the digits to the left. The top digit is 6, but there's nothing beneath it.
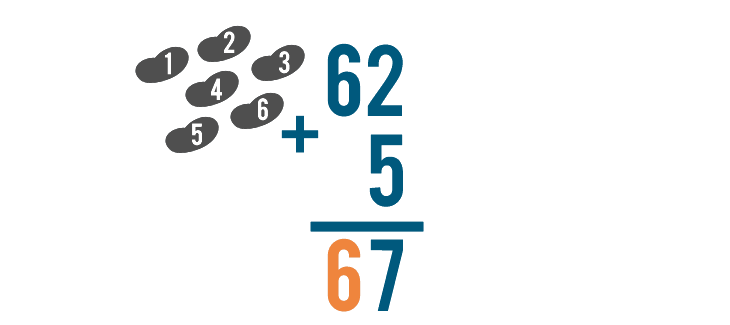
6 plus nothing is 6, so we'll write a 6 below the line.
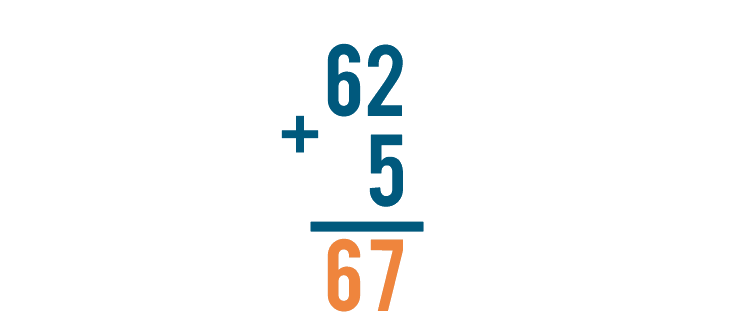
Our total is 67, or sixty-seven.

As you saw, stacked addition problems are always solved from right to left. This means that you always start by adding the digits on the right.
Try This!
Solve the addition problems below. Then, check your answer by typing it into the box.
Adding Very Large Numbers
Stacked addition can also be used for adding larger numbers. No matter how many digits are in the numbers you're adding, you add them the same way: from right to left.

Let's try adding two 3-digit numbers. We'll complete this expression: 213 + 406.

As always, we start with the digits on the far right. Here, that means we'll solve 3 + 6.

3 + 6 is 9, so we'll write 9 directly beneath the 3 and 6.
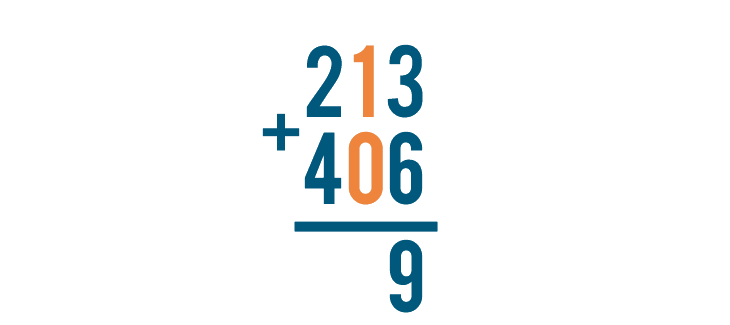
Next, we'll add the digits to the left of the ones we just added, 1 and 0.
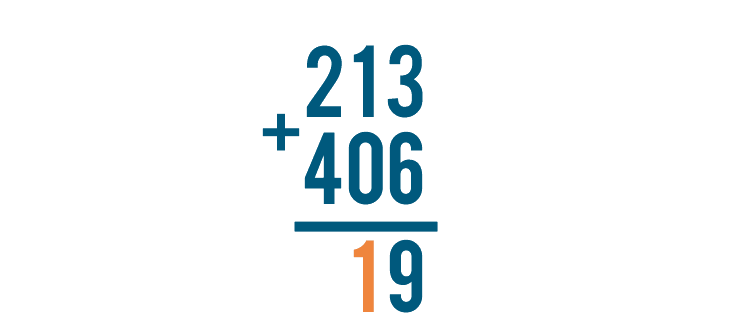
1 + 0 is 1, so we'll write 1 below the line. Make sure to put it directly beneath the digits we just added, to the left of the 9.
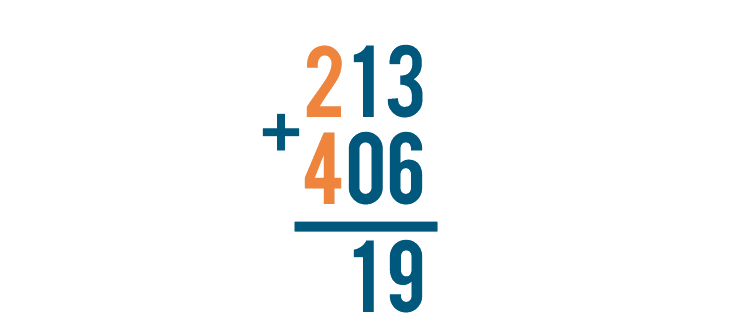
Finally, let's add the next set of digits, 2 and 4.
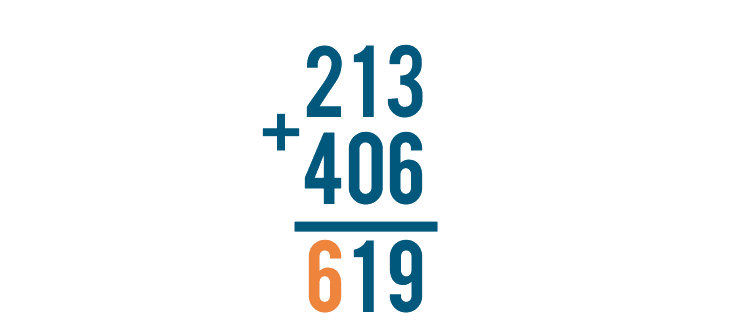
2 + 4 is 6. Let's write the 6 beneath the line, under the 2 and 4.

The problem is complete. Our total is 619, or six hundred nineteen. 213 + 406 = 619.

Try This!
Add these large numbers. Then, check your answer by typing it in the box.
Using Carrying
On the last page, you practiced adding vertically stacked numbers. Some problems need an extra step. For example, let's look at the following problem:
Our first step is to add the digits on the right— 5 and 9. However, you might notice there isn't room to write the sum, 14. When the sum of two digits in a math problem is greater than 9, the normal way of adding stacked numbers won't work. You'll have to use a technique called carrying.
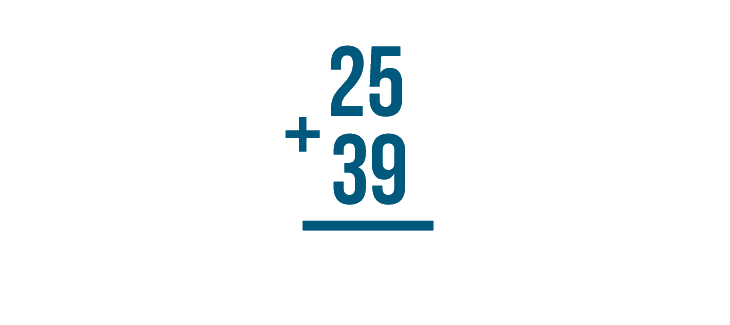
Let's see how it works. We'll try this problem, 25 + 39.
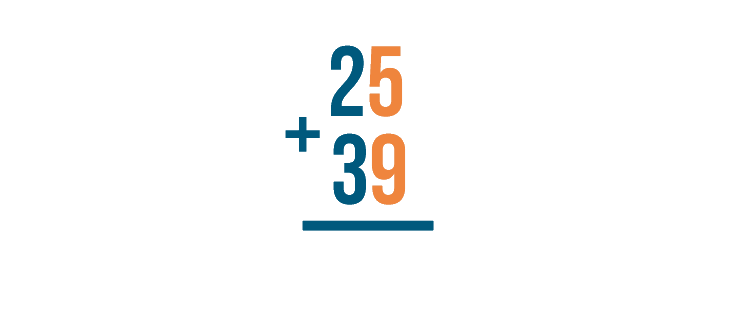
As usual, we'll start by adding the digits on the right. Here, that's 5 and 9.
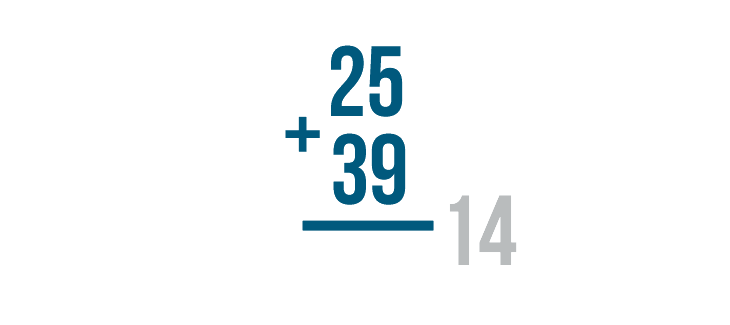
5 + 9 is 14, but there's no room to write both digits in 14 underneath the 5 and 9.
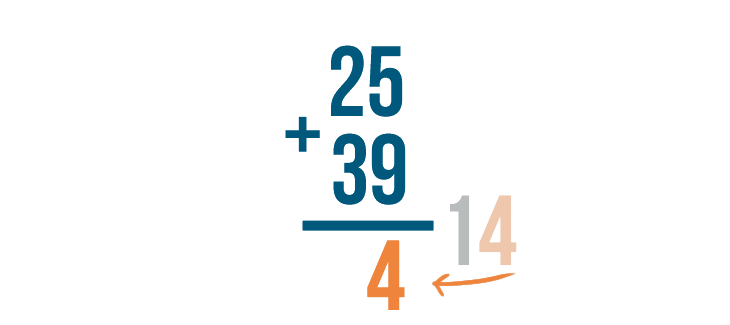
We'll write the right digit, 4, under the line...
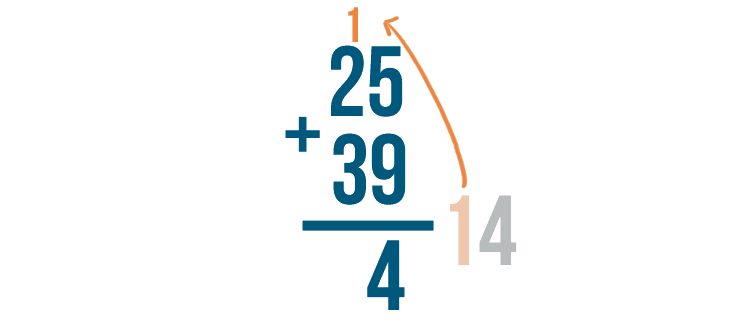
We'll write the right digit, 4, under the line... then we'll carry the left digit, 1, up to the next set of digits in the problem.
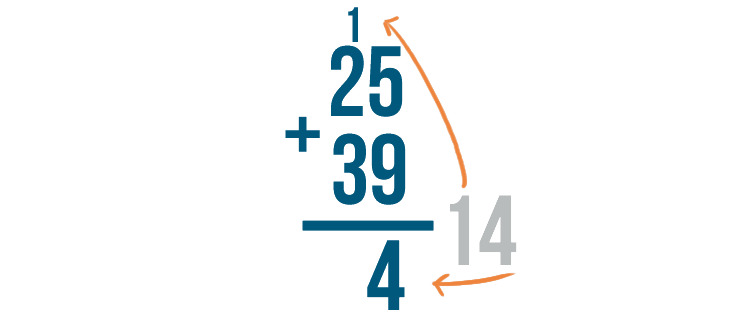
Do you see what we did? Our sum was 14. We put the 4 underneath the line, and carried the 1 and placed it above the next set of digits.
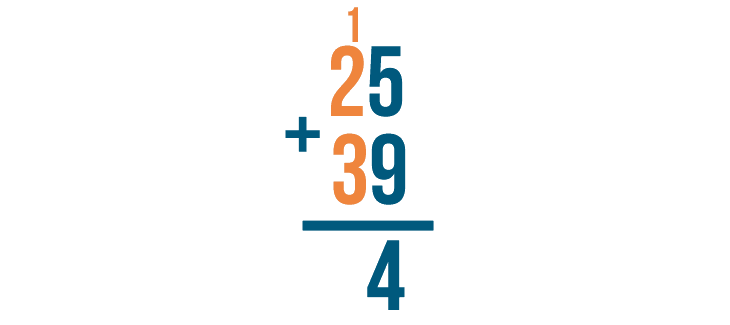
Next, we'll add the left digits. Since we carried the 1, we'll add it too.
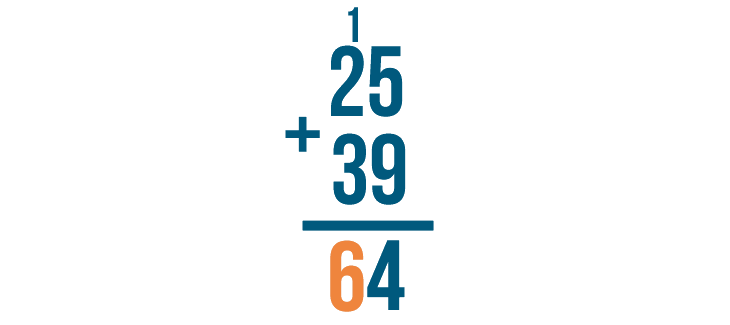
1 + 2 + 3 is 6, so we'll write 6 below the line.
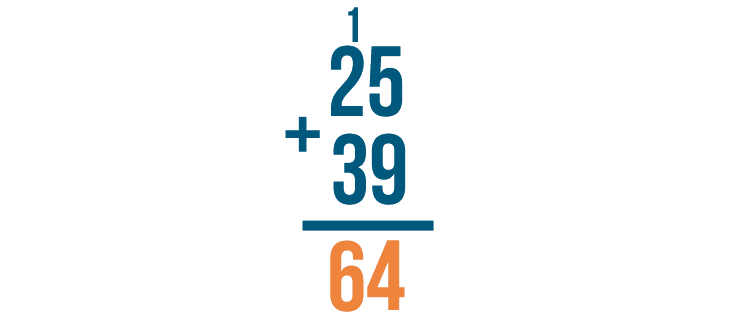
We're done. 25 + 39 = 64.
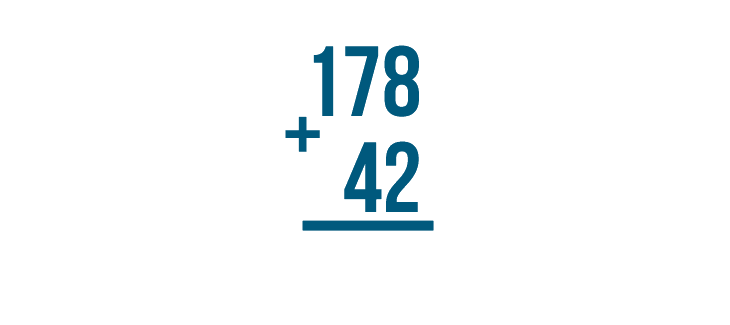
Let's practice with one more problem: 178 + 42.
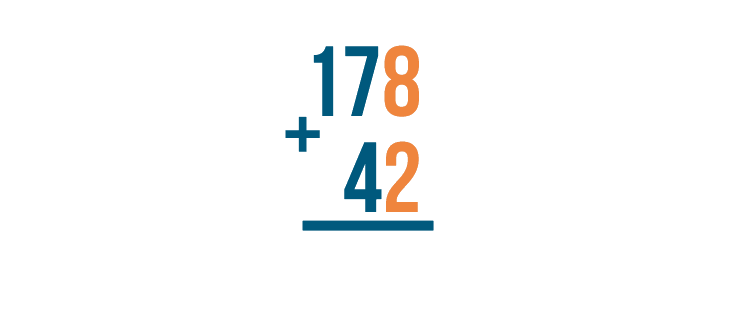
As always, start by adding the digits on the right. Here, that's 8 + 2.
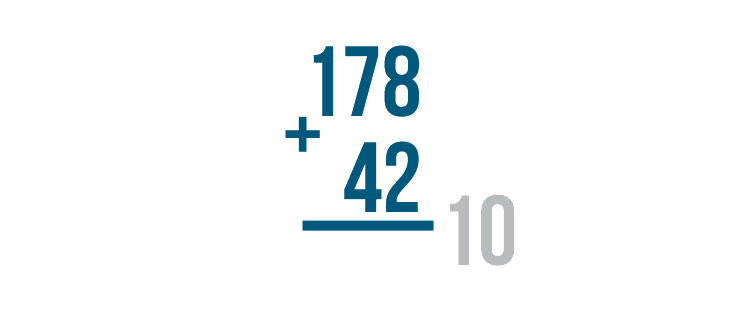
8 + 2 is 10, so it looks like we'll have to carry.
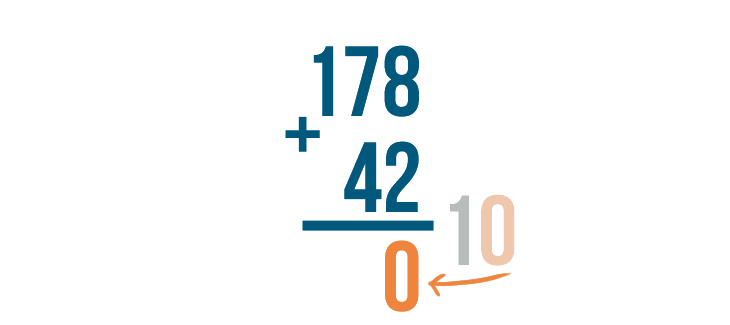
The 0 stays underneath the 8 and the 2.
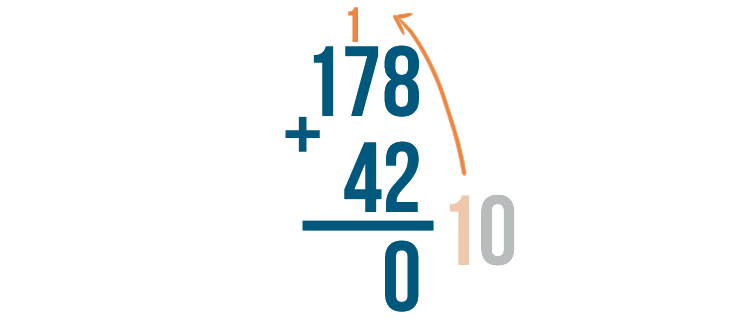
Carry the 1 and place it above the next set of digits to the left.
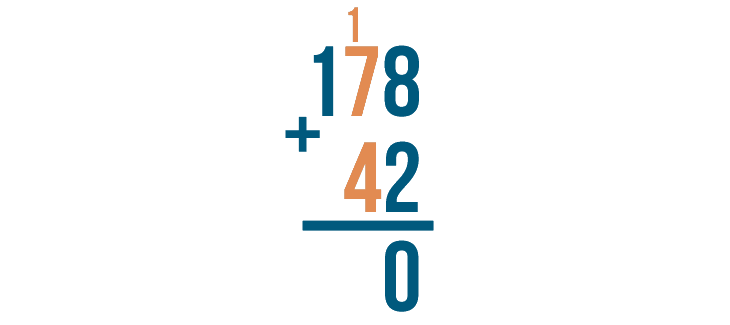
Now move left to add the next set of digits. Since we carried the 1, add it too.
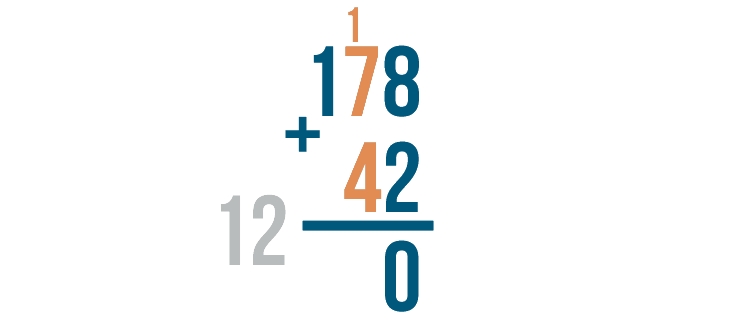
1 + 7 + 4 = 12.
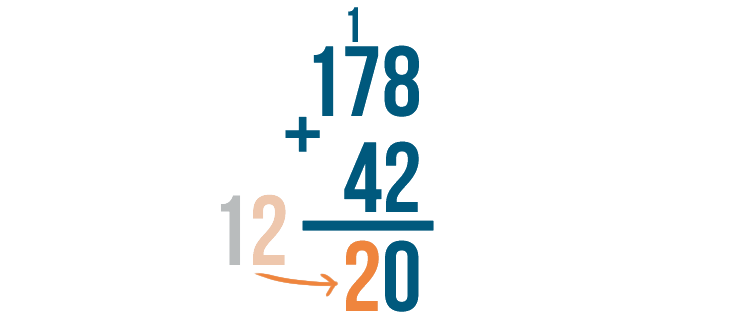
Put the right number, 2, under the digits we added.
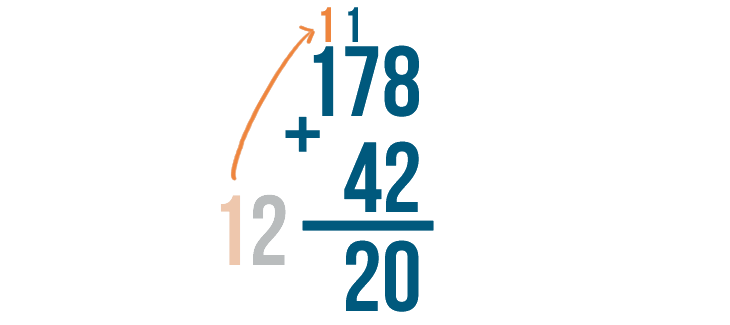
Carry the 1 and place it above the next column to the left.
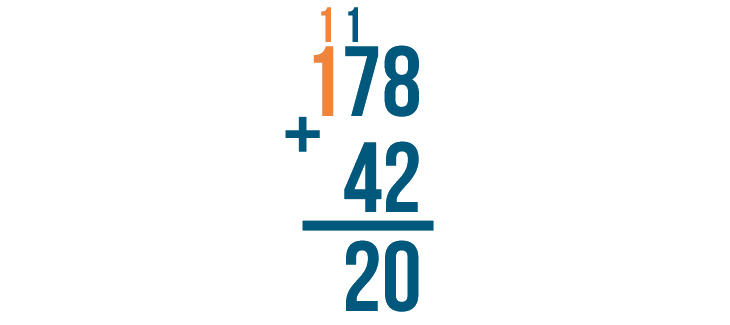
To finish, add this column. Remember to include the 1 we just carried.
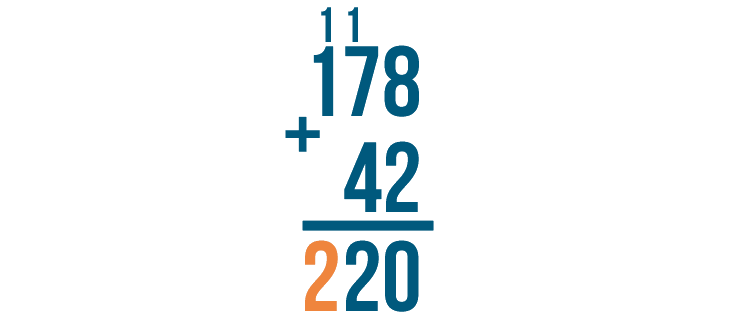
1 + 1 + nothing is 2, so we'll write 2 underneath the 1.
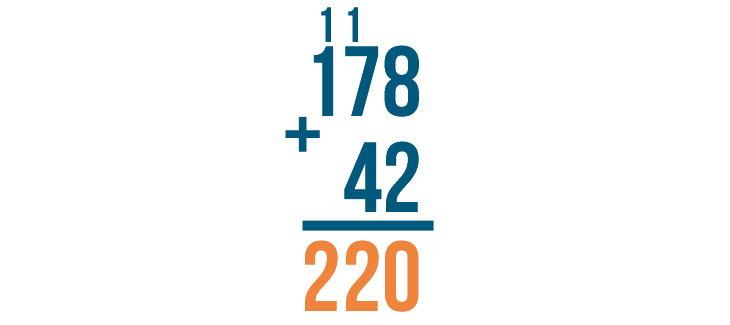
We're done. Our answer is 220. 178 + 42 = 220.

As you carry, be careful to keep track of the various numbers. If you're writing problems down, be sure to write the carried digits in small print above the column of digits to the left.
Try This!
Solve these problems by carrying. Then, check your answer by typing it in the box.
Practice!
Practice adding these problems. You'll have to use carrying to solve some of the problems. There are 4 sets of problems with 3 problems each.
Set 1
Set 2
Set 3
Set 4
/en/additionsubtraction/video-addition/content/



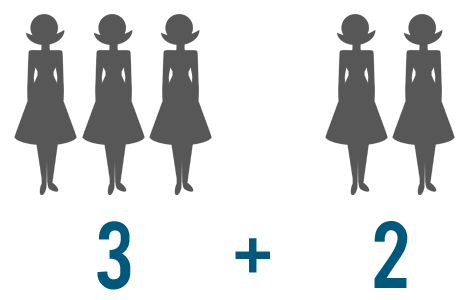
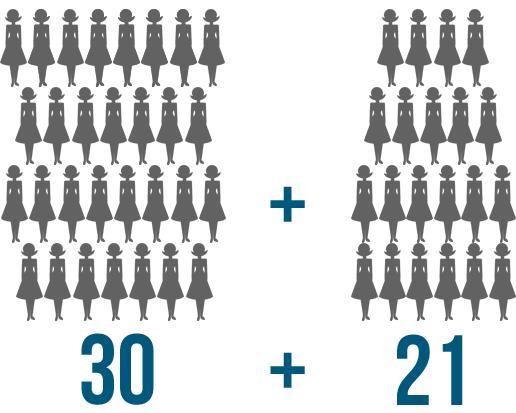
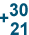 mean the same thing. They're just written differently.
mean the same thing. They're just written differently.