Os números decimais
Arredondamento ou aproximação decimal


/pt/os-numeros-decimais/problemas-com-divisao-de-decimais/content/
Quando trabalhamos com decimais, observamos que eles podem ter muitos números na parte decimal. No entanto, na vida cotidiana, não faz sentido trabalhar com todas estes dígitos, porque a partir de certo ponto eles representam partes tão pequenas que não afetam em nada se os desconsideramos.
Ao fazer alguns cálculos para a construção de um edifício, um engenheiro conclui que precisa de quilos de concreto. No entanto, bastará que este número tenha apenas três casas decimais para ele ter a quantidade de concreto exata. Qual deve ser a aproximação?
Os dígitos decimais necessários devem ser mantidos. Neste caso precisamos de três.

Se o próximo dígito à direita dos números necessários for maior ou igual a cinco, o último dígito necessário será aumentado em uma unidade. Se o número à direita dos números necessários for menor que cinco, o último número necessário não será alterado.
Nesse caso, o próximo dígito necessário é um seis. Como seis é maior que cinco, o oito é transformado em nove e o resto dos dígitos decimais é eliminado.
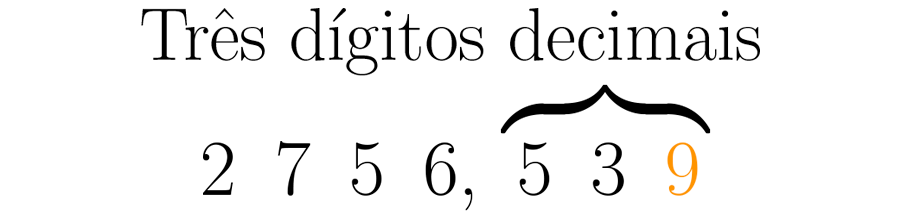
O engenheiro agora pode trabalhar com um número muito mais simples do que antes: .
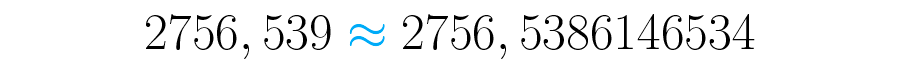
Que deve ser lido: " é aproximadamente igual a ".
Observe como o número se aproxima de duas casas decimais:
Devemos separar os dígitos decimais necessários, que neste caso são dois:
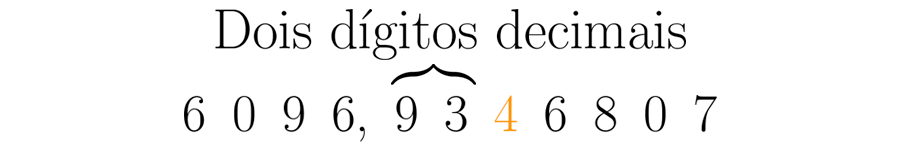
Lembre-se que o número que determina a aproximação é o próximo à direita dos dígitos requeridos, aqui desta vez é um quatro.
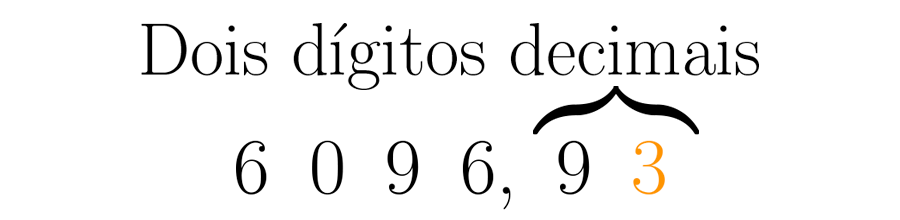
Podemos então afirmar que é aproximadamente igual a : . Desta forma, quando você precisar trabalhar com decimais no seu dia a dia, poderá ter o nível de precisão que cada situação exige.
/pt/os-numeros-decimais/como-usar-numeros-decimais-para-medir-coisas/content/