Os conjuntos matemáticos
Descrever e definir conjuntos


/pt/os-conjuntos-matematicos/o-que-e-um-conjunto/content/
Como vimos na página anterior, é possível representar graficamente os conjuntos através do diagrama de Venn. Mas para poder trabalhar com eles, é necessário também representá-los em linguagem matemática.
Usamos as chaves para representar e definir os conjuntos, e no seu interior estão os elementos que o formam separados por vírgula. Esta representação escrita é equivalente a representação gráfica dos diagramas de Venn.
Por exemplo, se você quer escrever o conjunto formado pelos elementos , , , e podemos usar as seguintes formas:
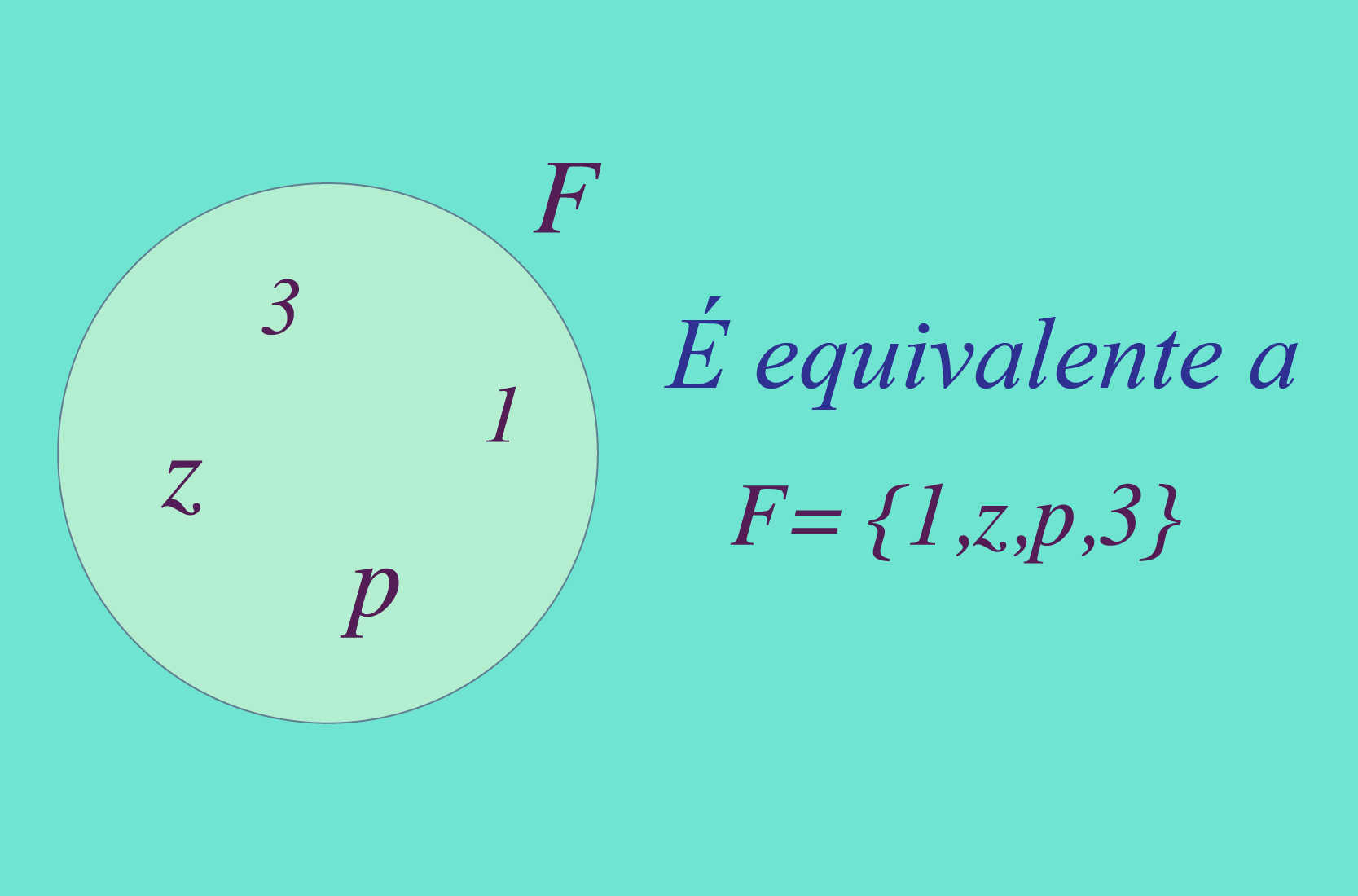
Para descrever os elementos de um determinado conjunto podemos mencioná-los um a um, o que é chamado de descrição por extensão. Definimos como o conjunto formado pelas cores do arco íris, desta forma vamos descrever o conjunto por extensão dessa forma:
Se um conjunto tem muitos elementos, podemos usar três pontos para descrevê-lo, por exemplo, o conjunto está formado pelos cem primeiros números e podemos representá-lo da seguinte forma.
Neste caso não mostramos os cem elementos que formam o conjunto, contudo, os três pontos representam todos os elementos que não escrevemos.
Em alguns casos, os conjuntos podem ter uma grande variedade de elementos e a descrição por extensão fica muito difícil. O que podemos fazer é descrever os conjuntos mencionando as características comuns dos elementos que o forma. Por exemplo, se é o conjunto formado por todos os países do mundo, podemos escrevê-lo assim:
Depois da barrinha | lemos "de modo que", assim, essa expressão acima pode ser lida desta forma: " é o conjunto dos , de modo que é um país". Neste caso o símbolo é usado simplesmente para representar os elementos do conjunto .
Algumas vezes os elementos que formam um conjunto devem satisfazer mais de uma condição, ou pelo menos uma de várias. Nestes casos usamos os conectivos disjunção e conjunção.
Observe o seguinte exemplo: Seja
Neste caso há duas condições para os animais que formam o conjunto: Ser mamífero ou voar. A disjunção é a letra "ou" que os conecta e significa que os elementos que formam o conjunto devem atender alguma destas condicionais ou as duas.
Neste caso por exemplo, a abelha tem a condição de voar, e por isso deve pertencer ao conjunto. O gato por sua vez, tem a condição de ser mamífero e por isso também pertence ao conjunto . O morcego tem as duas condições, já que é um mamífero que voa e por isto também pertence a .
Definimos o conjunto assim: Seja
Neste caso também existem duas condições mas estão unidas pela conjunção "e". Isto significa que os elementos que pertencem ao conjunto devem atender às duas condições ao mesmo tempo.
Como não existem números que atendem as duas condições ao mesmo tempo, concluimos que o conjunto não tem elementos.
Também é possível combinar os conectivos anteriores para estabelecer as condições que devem cumprir os elementos de um determinado conjunto. Por exemplo, seja
.
Como você pode ter percebido, na definição dos elementos do conjunto há duas condições: "ser maior ou igual a 4" e "ser menor que 8", como estas condições estão unidas por um "e" ambas devem ser cumpridas. Entretanto, a condição "ser maior ou igual a 4" está composta por duas condições unidas por uma disjunção, e isso significa que cumprem os números que são maiores que ou iguais a .
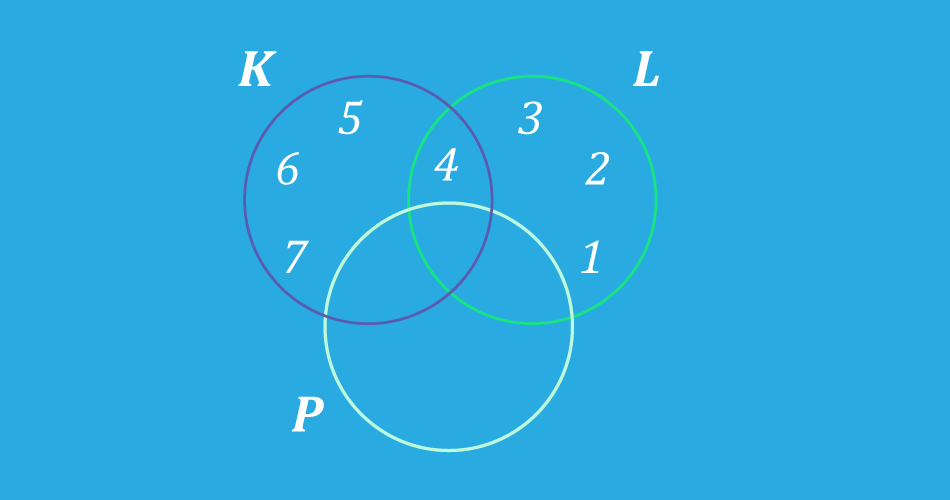
Abaixo, no diagrama de Venn, podemos ver a representação dos conjuntos que mostramos acima, e o conjunto
:
/pt/os-conjuntos-matematicos/tipos-de-conjuntos/content/