Los números
Orden en el conjunto de los números racionales


/es/los-numeros/algunas-propiedades-del-conjunto-de-los-numeros-racionales/content/
Los números racionales también representan cantidades, por lo tanto unos pueden representar más y otros menos, es decir, hay una relación de orden entre los mismos. Debes entonces estar en la capacidad de poder determinar cuándo un número fraccionario es mayor que otro.
Ubicamos las fracciones una al lado de la otra.
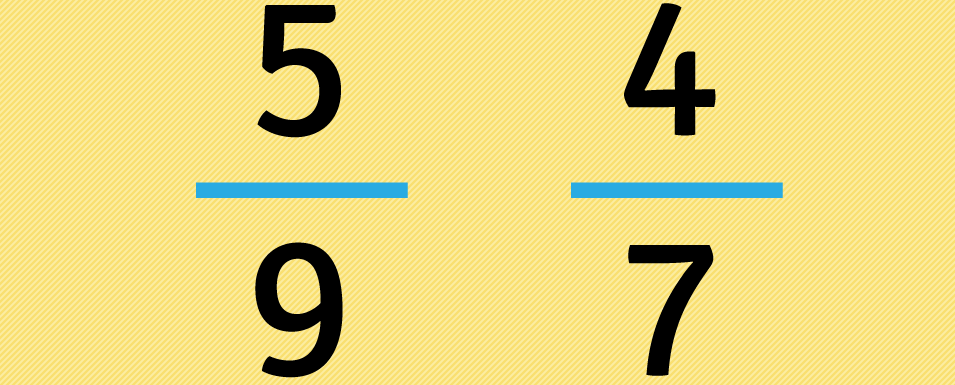
Sin tener en cuenta los signos menos (-) que pueda haber, multiplicamos el numerador de la primera fracción por el denominador de la segunda, luego ponemos el resultado de la multiplicación debajo de la primera fracción.

Nuevamente sin fijarnos en los , multiplicamos el numerador de la segunda fracción por el denominador de la primera, después ubicamos este resultado debajo de la segunda fracción.
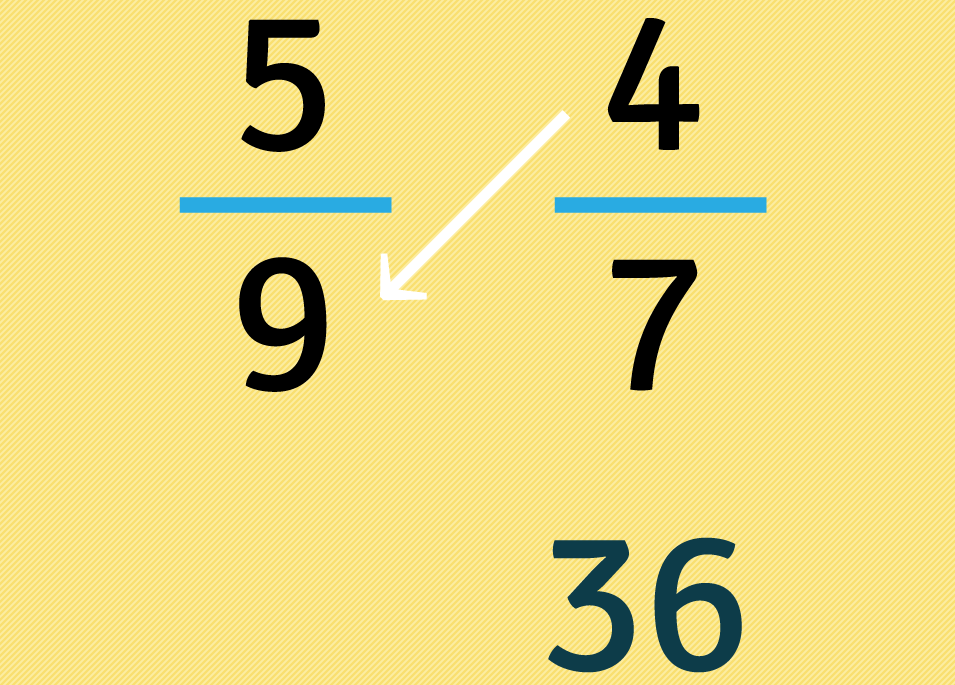
Ponemos, entre las fracciones, el mismo símbolo de orden que se deba poner entre las multiplicaciones hechas. En este caso como es menor que , ubicamos el símbolo entre ellos.
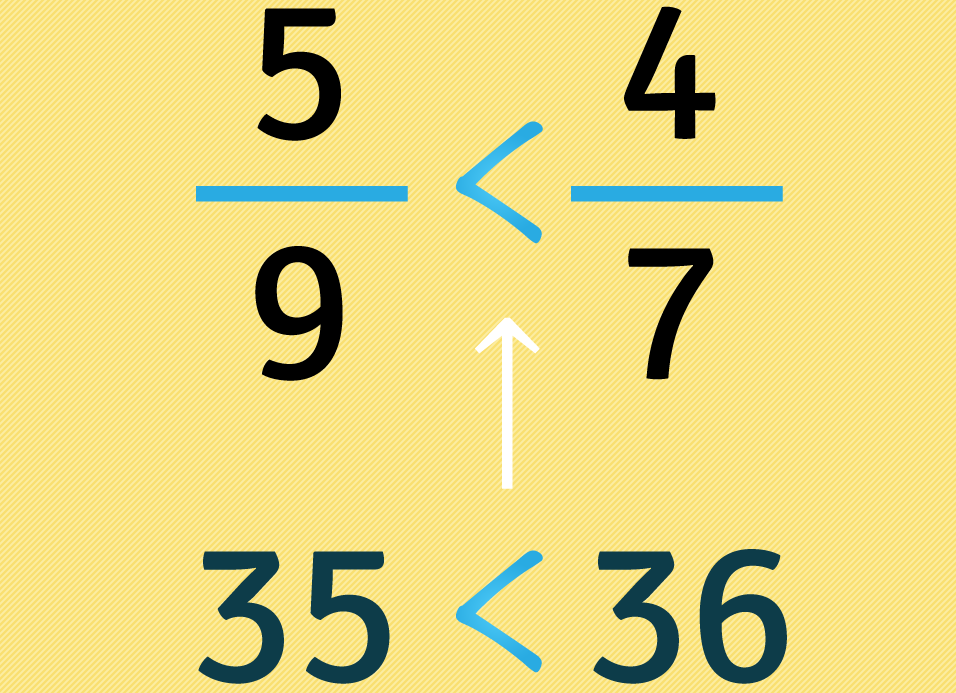
Por cada signo negativo que haya en la fracción que quede del lado mayor, cambiamos el sentido del signo ó que hayamos puesto. En este caso, al no haber signos en el número dejamos el símbolo tal y como está.
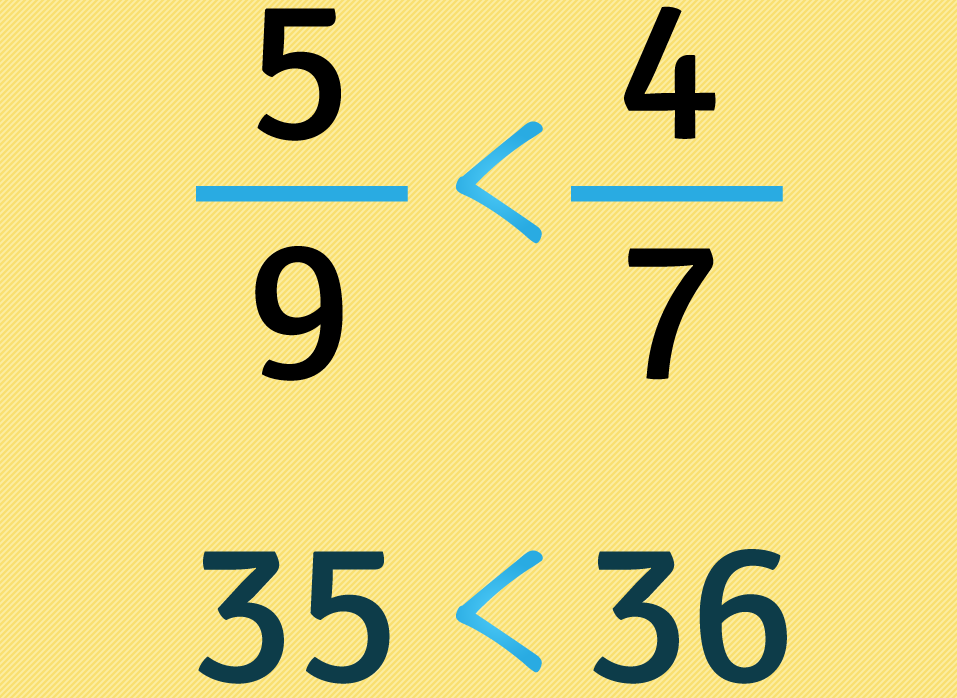
Podemos concluir entonces que representa más, o es mayor, que :
Veamos otro ejemplo, comparemos los racionales y :
Ubicamos los números uno al lado del otro.
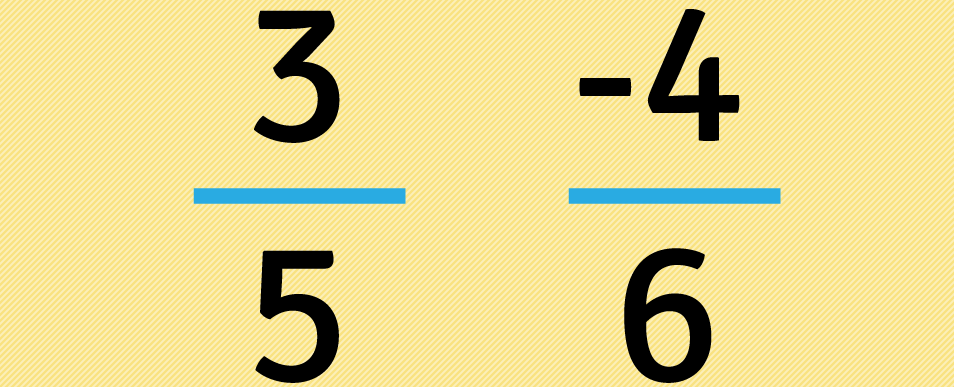
Sin tener en cuenta los signos , multiplicamos tres por seis: . Luego ponemos el resultado de la multiplicación debajo de la primera fracción.
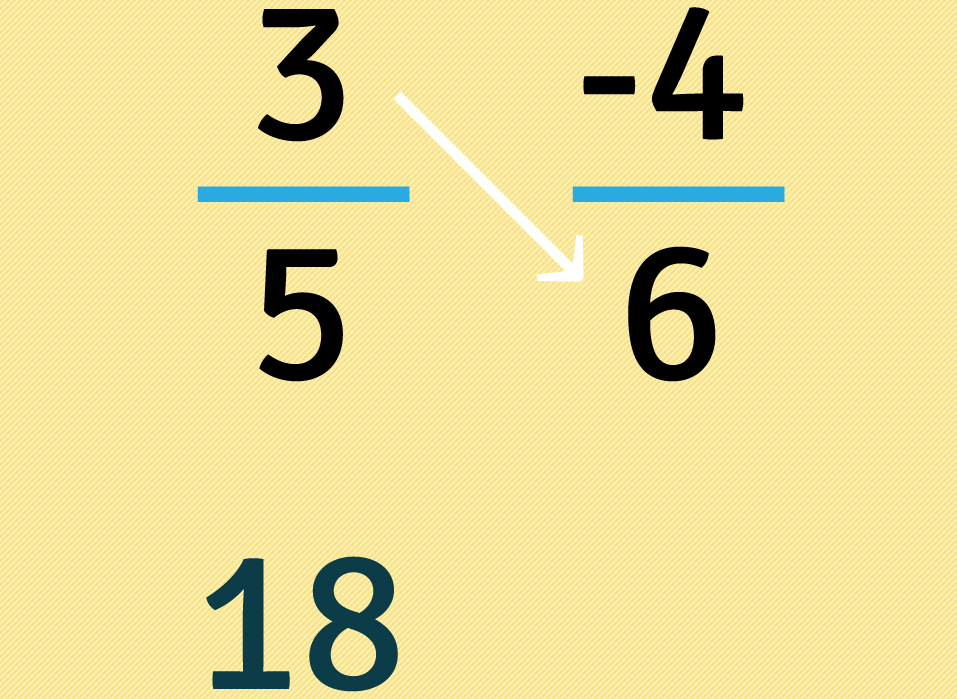
Nuevamente, sin tener en cuenta los signos , multiplicamos ahora cuatro por cinco: . Después ubicamos este resultado debajo de la segunda fracción.
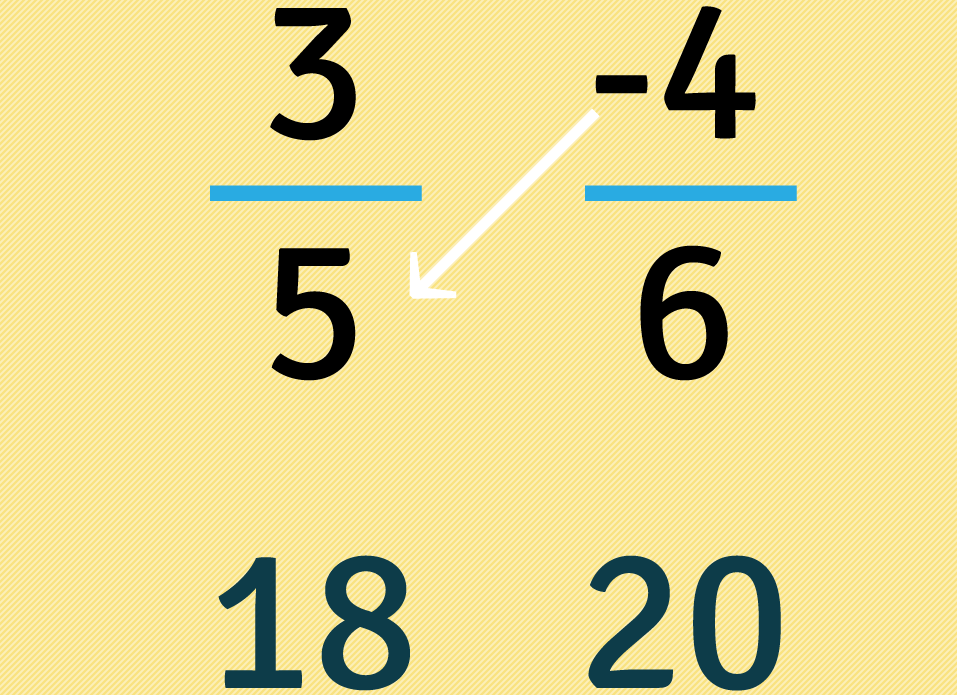
Como dieciocho es menor que veinte debemos usar el símbolo menor que así: . Ponemos entonces el mismo símbolo entre las fracciones: .
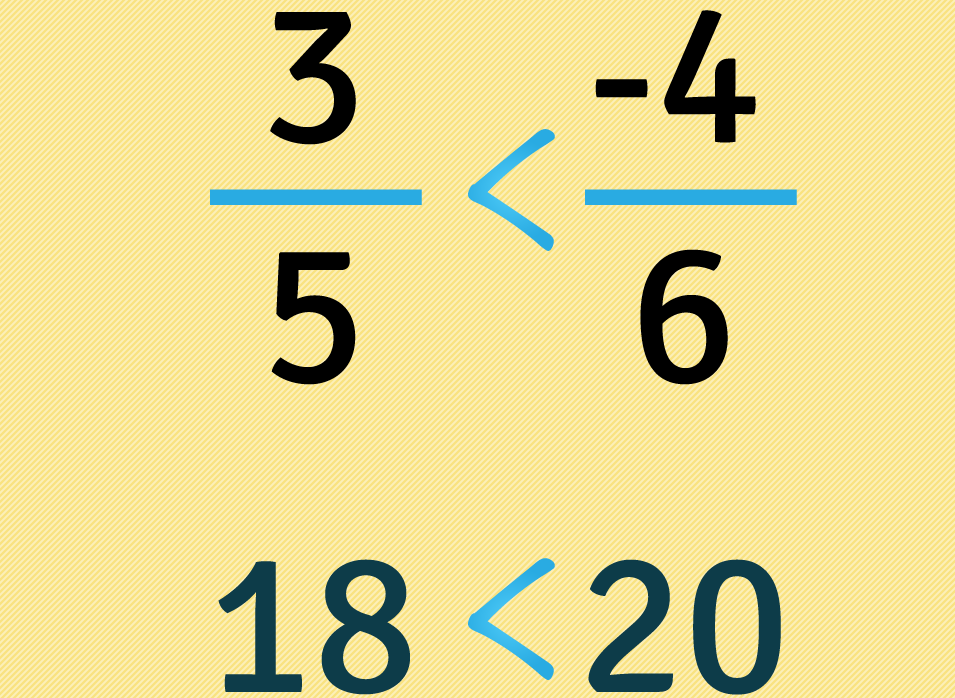
Como hay un signo en la fracción que quedo al lado mayor: cambiamos el sentido del signo una vez. Escribimos entonces entre las fracciones:
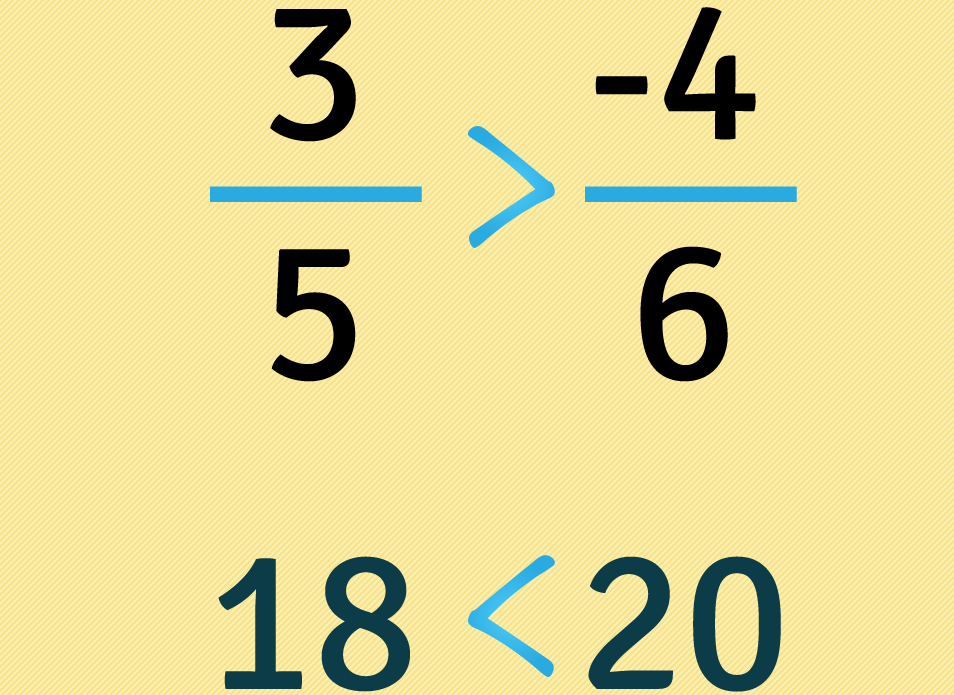
Podemos concluir que es mayor que . Esto era de esperarse pues los números negativos representan deudas y los positivos tenencias. Ahora lo mejor es practicar, así afianzarás lo aprendido y lo recordarás mucho más fácil.
/es/los-numeros/aprender-a-contar/content/