Fraccionarios
División de fracciones


/es/fraccionarios/problemas-con-multiplicacion-de-fracciones/content/
Solo nos queda por estudiar una operación con fracciones: la división. Aprende las distintas formas de efectuarla.
Ya sabes que la expresión es otra forma de representar la operación . Por lo tanto, cuando te enfrentes a una división del tipo puedes interpretarla así:
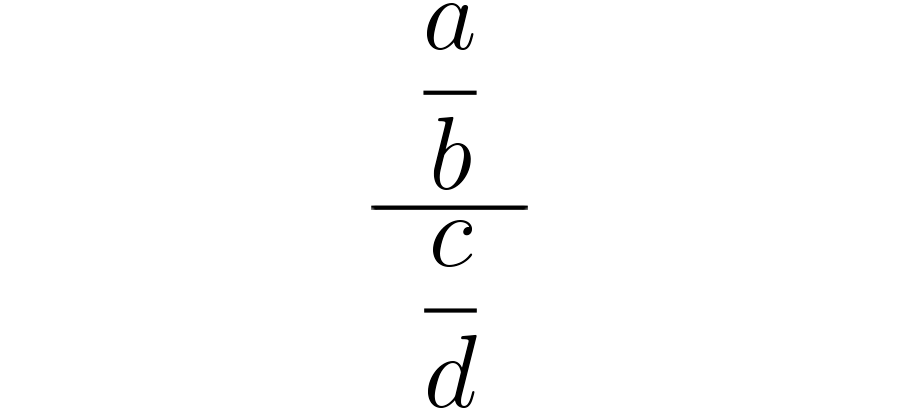
En muchos países se enseña a realizar y recordar cómo hacer esta operación por medio de un procedimiento que se denomina “ley de la oreja” o “ley de extremos y medios”.
Este procedimiento indica que se multiplican los extremos superior e inferior para obtener el numerador, y los números del medio para obtener el denominador.
En la siguiente imagen puedes ver como se hace:
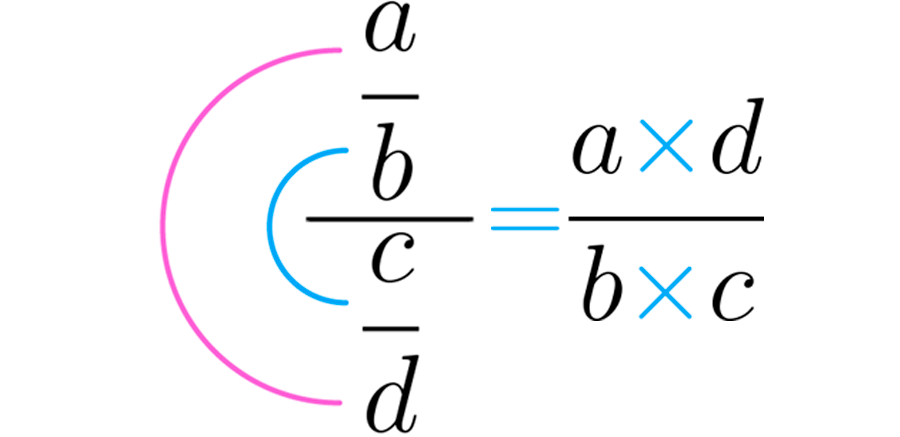
Ahora usemos este método para realizar la división :
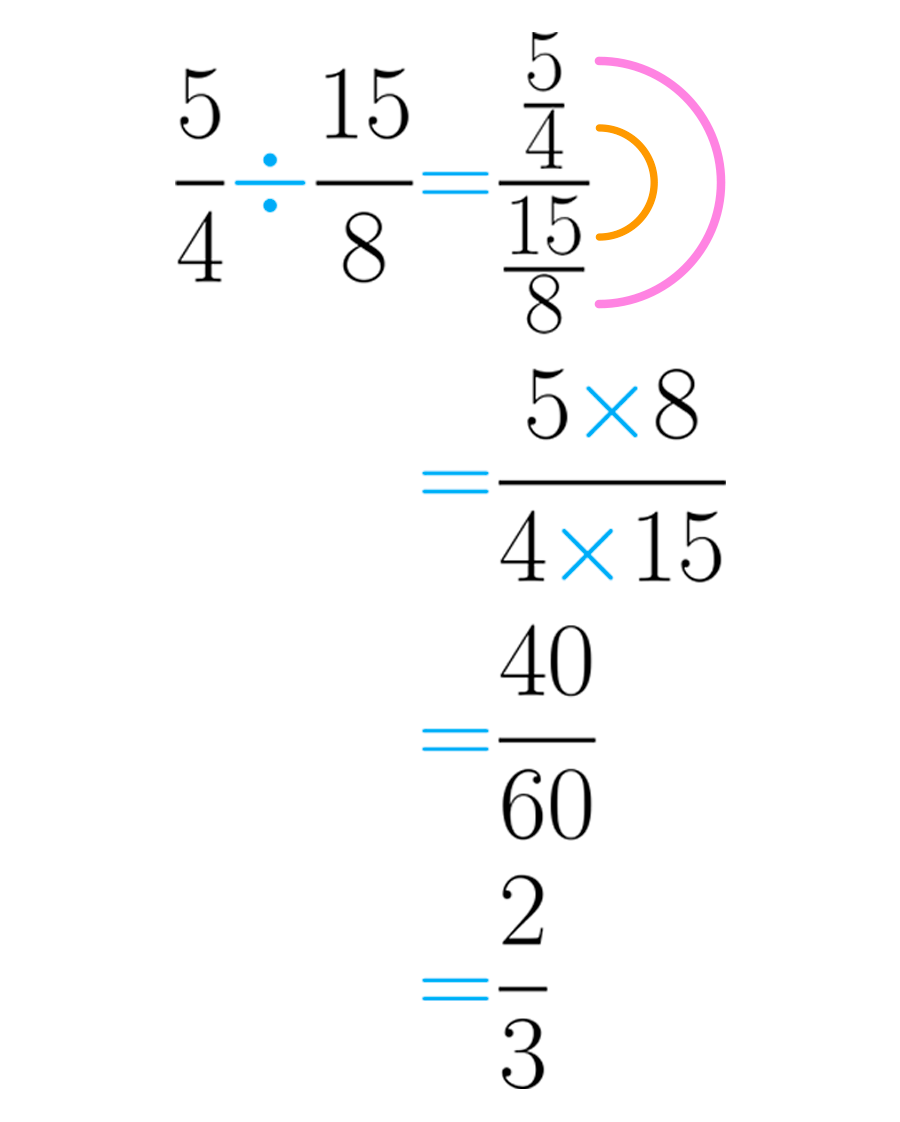
Puedes ver porque se le llama “oreja”, pues recuerda precisamente esta parte de nuestro cuerpo.
El resultado de la división es ; sin embargo, después de simplificar esta expresión, se obtiene la fracción que es irreducible.
Existe otra forma de realizar la división de fracciones: los “productos cruzados”. Con este método no es necesario poner las fracciones una sobre la otra, simplemente se multiplica numerador por denominador y denominador por numerador. Observa un ejemplo:
Realicemos la operación :
Primero multiplica el numerador del dividendo por el denominador del divisor. Este será el numerador de la respuesta. Después multiplica el denominador del dividendo por el numerador del divisor. Este resultado será el denominador del cociente:
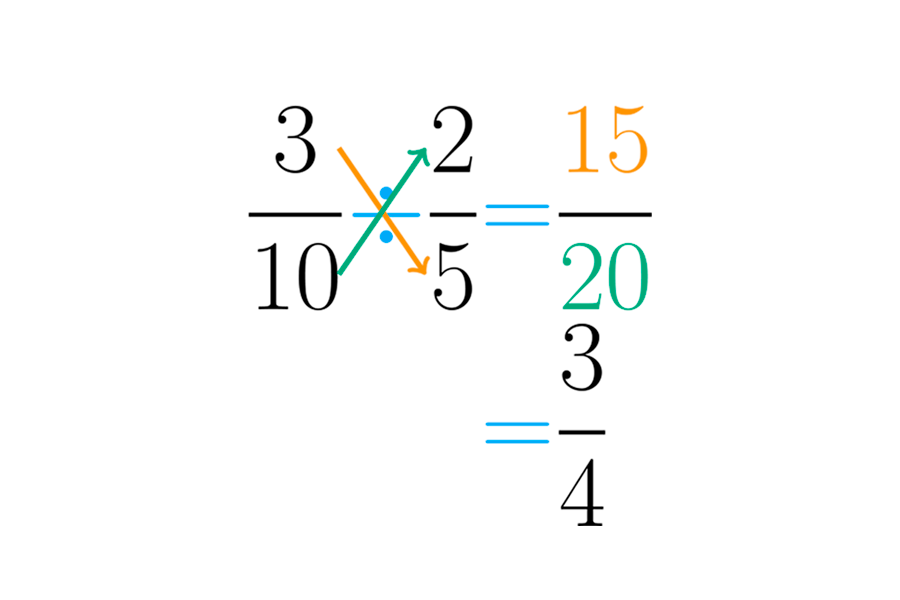
Por supuesto los resultados de obtenidos por la “ley de la oreja” y por los “productos cruzados” son siempre iguales.
/es/fraccionarios/problemas-con-division-de-fracciones/content/