Divisores y múltiplos
Problemas que se pueden resolver con divisores


/es/divisores-y-multiplos/propiedades-del-maximo-comun-divisor/content/
Aprende a usar el concepto de máximo común divisor para solucionar problemas. !Entiende como se hace y luego practica mucho!
Observa la siguiente situación: un carpintero tiene dos trozos de madera de y centímetros cada uno. Desea dividirlos en partes iguales de la mayor longitud posible sin que le sobre nada, ¿de cuántos centímetros debe ser cada una de las partes?
Antes de tratar de resolver el problema, analicémoslo un poco. Supongamos por ejemplo que decide hacer trozos de centímetros. Al dividir el trozo de obtendría dos, pero al dividir el de tendría una parte de centímetros y otra de , que desperdiciaría puesto que quiere que todas las partes sean iguales.
Para que no se desperdicie nada, la medida de las divisiones debe ser divisor común de y . Además, las partes deben ser lo más grandes posible, así, el divisor que buscamos es el mayor; es decir, el máximo común divisor. Descomponemos los números y para calcular su

De las descomposiciones y , se observa que los factores primos comunes (con el menor exponente) son y Luego, . Se deduce entonces que el carpintero debe hacer partes de centímetros cada una.
Observa que el número de balones en cada caja debe ser un divisor común, por ejemplo: si se empacan siete balones en cada caja se tendrían que usar cajas para los balones rojos y no sobra ninguno. Sin embargo para los verdes se necesitan: y sobran , esto quiere decir que quedaría una caja con seis balones verdes. En cambio, si el número de balones en cada caja es un divisor común de y se empacarán los balones y no sobrarán de ningún color.
Ahora bien, sabemos que el número de balones en cada caja debe ser divisor de y de , pero también debe ser el mayor posible. Esto es, estamos buscando su
Como puedes ver en la imagen de la derecha las descomposiciones primas son y .
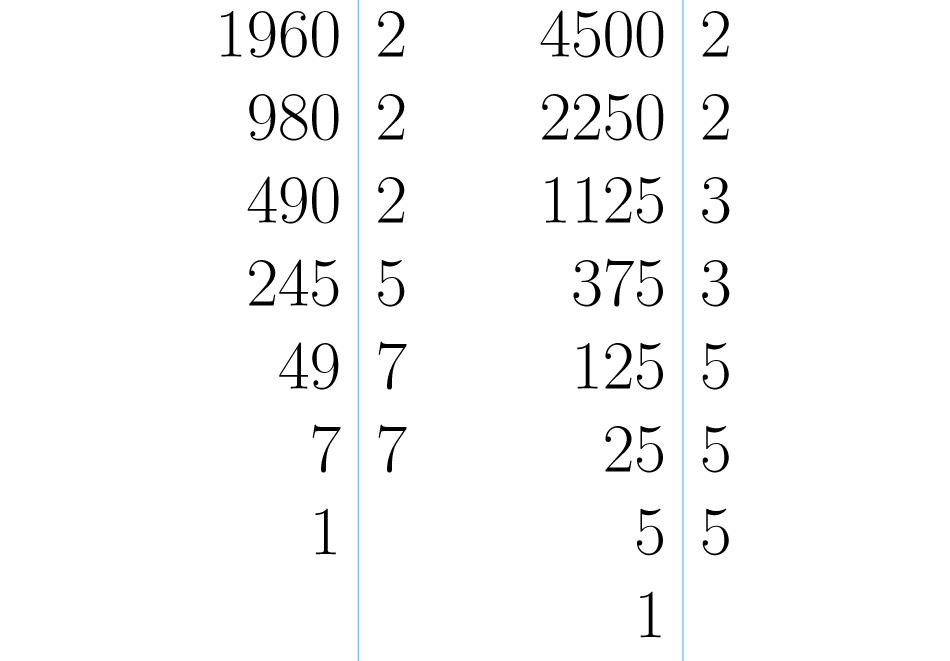
Los factores primos comunes con menor exponente son y , entonces . Esto quiere decir que se deben empacar balones en cada caja. De esa forma se asegura que habrá el mismo número en cada una y, además, no habrá un número más grande que permita una distribución sin que sobren balones de algún color.
/es/divisores-y-multiplos/que-son-los-multiplos/content/